1 2 Построение планов ускорений.

Определяем ускорение точки А кривошипа по формуле

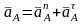Здесь , 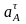- нормальное и тангенциальная составляющие. В нашем примере 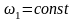, поэтому Нормальное ускорение определяется выражением 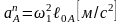Этот вектор направлен параллельно ОА к центру вращения кривошипа (от точки А к точке 0 на звене).Назначаем масштабный коэффициент плана ускорений и определяем длину вектора Р_aa который будет представлять ускорение точки А.

Из полюса плана ускорений P_a откладываем отрезок 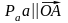рис. 2.9. Здесь стрелка внизу показывает направление вектора от точки А к точке 0 на звене.Для определения ускорения точки В опять разложим движение шатуна, как при построении плана скоростей. Тогда будем иметь

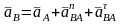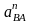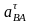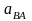В этом уравнении и -нормальная и тангенциаль­ная составляющие относительного ускорения . Нормальная состав­ляющая вычисляется по формуле

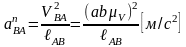
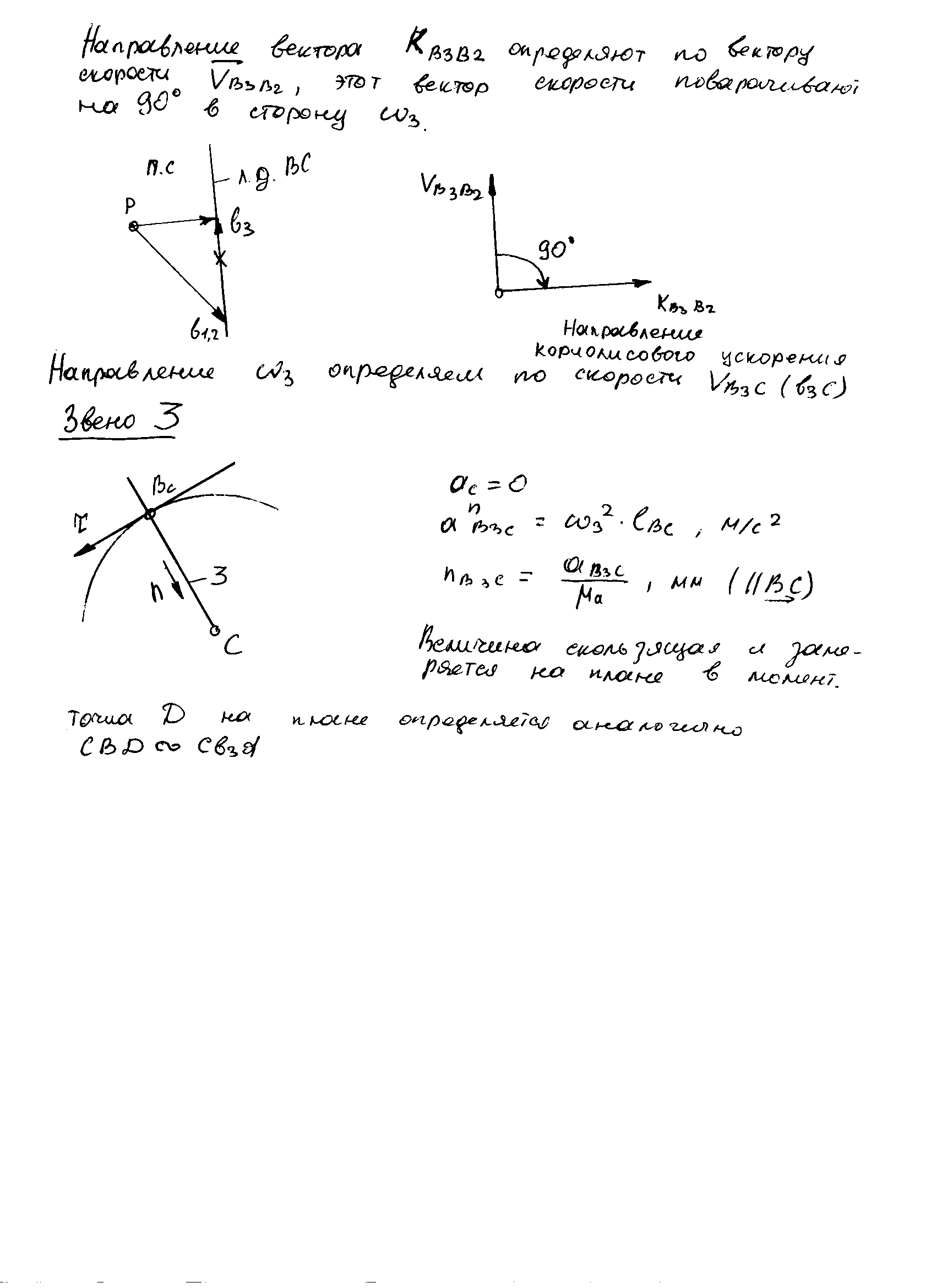Здесь ab - отрезок плана скоростей. Начало и конец вектора на плане ускорений обозначим точкамиа и n₂ ; n -говорит, что отложено нормальное ускорение, индекс 2 - что рассматривалось звено 2. Полученное векторное уравнение может быть решено графически построением плана ускорений. Для этого из полюса Р_a проводим направление вектора абсолютного ускорения точки В параллельно направляющим ползуна b и далее строим векторную сумму по правой части уравнения. Пересечение известных по направлению векторов 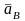и 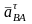,и дает решение - точку "в" плана ускорений. Отрезок n₂b в принятом масштабе представляет вектор , величина которого равна 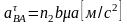Зная величину и направление тангенциальной составляющей отно­сительного ускорения точек В и А, можно определить величину и направление углового ускорения шатуна 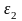. Его величина определяется выражением Для определения направления - вектор показываем выходящим из точки В на звене.

1 5 Свойства планов скоростей.

Началом векторов абсолютных скоростей является одна точка P_V - полюс плана скоростей. Вытекает из определения.

2. Отрезки, соединяющие концы векторов абсолютных скоростей, при принятом масштабном коэффициенте 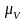представляют относительные скорости точек.

3. Одноименные фигуры на звене и плане скоростей подобны, а одноименные отрезки пропорциональны и повернуты на 90° в сторону вращения звена.

4. Всем точкам, скорость которых равна 0, на плане скоростей отвечает одна точка-полюс P_V.

Свойства планов ускорений.

Эти свойства аналогичны свойствам планов скоростей и доказы­ваются аналогично.

1. Векторы абсолютных ускорений всех точек берут начало в одной точке - полюсе P_a. Вытекает из определения.

2. Отрезки соединяющие концы векторов абсолютных ускорений, при принятом масштабном коэффициенте и представляют относительные ускорения точек. Например,

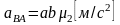
3. Одноименные фигуры на звене и плане ускорений подобны, а одноименные отрезки пропорциональны и повернуты в сторону углового ускорения звена на одинаковых угол 180°- .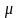

4. Всем т очкам, ускорение которых равно нулю, на плане ускоре­ний соответствует одна точка - полюс Р_a.

1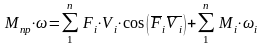 6 Масштабный коэффициент – это отнош единиц натуры к мм чертежа, величина размерная. Все масшт коэф опред до 3-5 знака после запятой. Например µ_v – масштаб коэф построй планов скоростей.

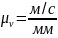
V_b – действ скорость точки, м/с

pb – вектор скорости точки, мм

1 7) Задачи динамического анализа машин и механизмов.При рассмотрении вопросов кинематического анализа механизмов мы всегда предполагаем движение входных звеньев заданным. Движение выходных звеньев изучается в зависимости от заданного движения входных. При этом силы, действующие на звенья механизма, и силы, возникающие при его движении, нами не изучаются. Таким образом, при кинематическом анализе исследование движения механизмов ведется с учетом только структуры механизмов и геометрических соотношений между размерами их звеньев. динамический анализ механизмов имеет своими задачами: а) изучение влияния внешних сил, сил веса звеньев, сил трения и массовых сил (сил инерции) на звенья механизма, на элементы звеньев, на кинематические пары и неподвижные опоры и установление способов уменьшения динамических нагрузок, возникающих при движении механизма; б) изучение режима движения механизма под действием заданных сил и установление способов, обеспечивающих заданные режимы движения механизма. Первая задача носит название силового анализа механизмов, а вторая задача — название динамики механизмов. В динамический анализ механизмов может быть включен и ряд других задач, имеющих важное техническое значение, а именно: теория колебаний в механизмах, задача о соударении звеньев механизмов и др. Но эти вопросы являются предметом изучения в специальных курсах, так как при решении их необходимо применять методы теории упругости, а в теории механизмов и машин задачи решаются обычно в предположении, что звенья механизмов являются абсолютно жесткими. Первая из указанных задач динамики механизмов имеет своей целью определение внешних неизвестных сил, действующих на звенья механизма, а также усилий (реакций), возникающих в кинематических парах при движении механизма. К внешним силам, например, относятся давление рабочей смеси (газа или жидкости) на поршень кривошипно-ползунного механизма двигателя внутреннего сгорания, парового двигателя, компрессора, вращающий момент, развиваемый электродвигателем на валу рабочего механизма, и др. Некоторые силы возникают в результате движения механизма. К этим силам, например, относятся силы трения при движении, силы сопротивления среды и т. д. Некоторые силы, как, например, динамические реакции в кинематических парах, возникают при движении вследствие инерции звеньев. Изучение природы СИЛ требует не только теоретического, но и экспериментального исследования. С помощью современных измерительных приборов можно весьма точно определять различные силы, действующие на отдельные звенья механизма, и выявлять их зависимости от различных факторов. Если известны внешние силы, действующие на звенья механизма, и известны законы движения всех его звеньев, то можно методами, излагаемыми в механике, определить силы трения и реакции связей в кинематических парах, силы сопротивления среды, силы инерции звеньев и другие силы, возникающие при движении механизма, и тем самым произвести так называемый силовой расчет механизма. К первой задаче динамического анализа механизмов относится также вопрос об устранении дополнительных динамических нагрузок от сил инерции на опоры механизма соответствующим подбором масс звеньев. Этот вопрос рассматривается в теории уравновешивания масс в механизмах. Вторая задача имеет своей целью определение мощности, не обходимой для воспроизведения заданного движения машины или механизма, я изучение законов распределения этой мощности на выполнение работ, связанных с действием различных сил на механизм, а также решение вопроса о сравнительной оценке механизмов с помощью коэффициента полезного действия, характеризующего степень использования общей энергии, потребляемой машиной или механизмом, на полезную работу. К этой же задаче относится вопрос об определении истинного движения механизма под действием приложенных к нему сил, т. е. задачи о режиме его движения, а также вопрос о подборе таких соотношений между силами, массами и размерами звеньев механизма или машины, при которых движение механизма или машины было бы наиболее близким к требуемому условию рабочего процесса. Эта задача обычно носит название теории движения машины или механизма под действием заданных сил