
- •1.Основные понятия.
- •3) Кинематические цепи. Кинематические соединения
- •4) Механизмы плоские и пространственные. Число свободы механизма и его определение.
- •8,Рычажный механизм.
- •9) Понятие термина машина, классификация машин
- •10 Основные методы кинематического анализа.
- •11 Графоаналитический метод кинематического анализа - метод планов скоростей и ускорений.
- •1 2 Построение планов ускорений.
- •1 5 Свойства планов скоростей.
- •1 8 Приведение сил и масс. Динамические модели машины.
- •22 Виды зубчатых механизмов
3) Кинематические цепи. Кинематические соединения
Классификация кинематических пар. Кинематические пары (КП) классифицируются по следующим признакам:
1. по виду места контакта (места связи) поверхностей звеньев:
• низшие, в которых контакт звеньев осуществляется по плоскости или поверхности ( пары скольжения );
• высшие, в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием). 2. по относительному движению звеньев, образующих пару: • вращательные; • поступательные; • винтовые; • плоские; • сферические. 3. по способу замыкания (обеспечения контакта звеньев пары): • силовое (за счет действия сил веса или силы упругости пружины); • геометрическое (за счет конструкции рабочих поверхностей пары). 1. по числу условий связи, накладываемых на относительное движение звеньев ( число условий связи определяет класс кинематической пары ); 2. по числу подвижностей в относительном движении звеньев. Кинематическая цепь – это система звеньев, связанных между собой кинематическими парами.Кинематические цепи могут быть:простыми (цепь, в которой каждое звено входит не более чем в 2 кин. пары) и сложными ( цепь, в которой хотя бы одно из звеньев образует более 2 кин.пар).
4) Механизмы плоские и пространственные. Число свободы механизма и его определение.
Плоский механизм- мех. , в котором все точки и звенья перемещаются в плоскостях // между собой.
Пространственный мех.- мех., в котором все точки и звенья перемещаются в плоскостях не // между собой. W число степеней свободы мех-ма. W=1 – для плоских мех-мов Wне= 1 – для пространственных мех-мов Определение числа степеней свободы мех-ма W=3*n-2*P5-P4- формула Чебышева для плоских мех-мов. W-число степеней свободы n-число подвижных звеньев Р5-число пар 5-го класса мех-ма Р4-число пар 4-го класса мех-ма Для плоских мех-мов если Wне= 1 то допущена ошибка, либо присутствуют звенья, создающие лишнюю степень свободы.
5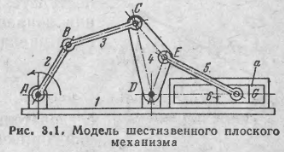
 )
Структурный
синтез механизмов на примере плоского
механизма
Основной
принцип образования механизмов был
впервые сформулирован в 1914 г. русским
ученым Л. В. Ассуром. Им был продолжен
и развит метод образования механизмов
путем последовательного
наслоения кинематических цепей,
обладающих определенными структурными
свойствами.
Этот метод
легко проследить, рассматривая какой
либо конкретный механизм, например
механизм, показанный на рис: 3.1. Этот
механизм имеет
пять подвижных звеньев, образующих
семь кинематических пар 5 класса.
Следовательно, по формуле
Чебышева (2.5)
число его
степеней
свободы равно W=3*n-2*P5=3*5-2*7=1т.
е. механизм, показанный на рис. 3.1,
обладает одной степенью свободы. Выберем
в качестве начального звено
2. Тогда
механизм будет состоять из начального
звена 2,
обладающего
одной степенью свободы,
стойки 1
и звеньев,
образующих кинематическую цепь,
состоящую из звеньев 3,
4, 5 и 6.
Процесс
образования
этого механизма можно представить как
последовательное присоединение к
начальному звену 2
и к стойке
1 кинематической
цепи, состоящей из звеньев З
и 4.
Тогда получим
четырехзвенный механизм АВCD,
обладающий
одной степенью
свободы. Далее к
звену 4
механизма
AВСD
и стойке 1
присоединим
кинематическую цепь, состоящую из звена
5 и
ползуна 6.
Тогда получим
шестизвенный механизм, обладающий
также одной степенью свободы.
Нетрудно теперь
установить определенную закономерность
процесса образования механизма. В самом
деле, любой механизм имеет одно
неподвижное звено (стойку).
У механизма,
показанного на рис. З.1, стойкой будет
звено 1. далее,
механизм должен иметь число начальных
звеньев, равное числу его степеней
свободы. В
нашем случае механизм (рис. 3.1) обладает
одним начальным звеном 2,
так как
степень свободы механизма согласно
(3.1) равна W=1
Так как после присоединения звеньев
3, 4, 5 и
б число степеней свободы всего механизма
осталось равным W=1,
то, следовательно, кинематическая цепь,
состоящая из звеньев 3,
4, 5 и 6,
присоединенных к начальному звену 2
и стойке 1,
обладает
нулевой степенью свободы относительно
тех звеньев, к которым эта цепь
присоединяется. При последовательном
присоединении групп
необходимо
руководствоваться определенными
правилами. При образовании механизма
с одной степенью свободы первая группа
присоединяется свободными элементами
звеньев к начальному звену и к стойке.
Последующие группы могут присоединиться
к любым звеньям
полученного механизма только так, чтобы
звенья группы обладали
подвижностью
друг относительно
друга. Пусть,
например,мы
имеем
четырехзвенный механизм
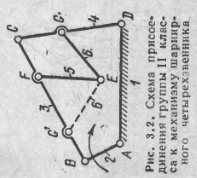
АВСD
(рис. 3.2),
образованный
начальным
звеном 2,
стойкой 1
и группой,
состоящей из
звеньев 3 и
4. Следующая
группа, состоящая из звеньев 5
и 6,
может быть
присоединена
к любым двум разным звеньям механизма,
например к звеньям 3
и 4
(рис. 3.2), но
не к одному и тому же звену. Так, например,
если присоединить звенья 5
и 6
к одному и
тому же звену 3
(рис. 3.2). то
контур FEG’,
образованный
звеньями 3,
5 и 6, будет
жестким, т. е. будет фермой.Нетрудно
видеть, что
для того,
чтобы после
присоединения группы ее звенья имели
подвижность относительно тех звеньев,
к которым группа присоединена, необходимо,
чтобы замкнутый контур, образованный
звеньями группы и звеньями, к которым
она присоединится, был подвижным
контуром. Так, на
рис. 3.2 контур
GСFЕ
будет обладать
подвижностью. Нетрудно видеть, что для
того, чтобы
такой контур
обладал подвижностью, необходимо, чтобы
звенья контура входили бы не
менее чем
в четыре
кинематические
пары (пары F,
Е,G
и С на рис.
3.2).
)
Структурный
синтез механизмов на примере плоского
механизма
Основной
принцип образования механизмов был
впервые сформулирован в 1914 г. русским
ученым Л. В. Ассуром. Им был продолжен
и развит метод образования механизмов
путем последовательного
наслоения кинематических цепей,
обладающих определенными структурными
свойствами.
Этот метод
легко проследить, рассматривая какой
либо конкретный механизм, например
механизм, показанный на рис: 3.1. Этот
механизм имеет
пять подвижных звеньев, образующих
семь кинематических пар 5 класса.
Следовательно, по формуле
Чебышева (2.5)
число его
степеней
свободы равно W=3*n-2*P5=3*5-2*7=1т.
е. механизм, показанный на рис. 3.1,
обладает одной степенью свободы. Выберем
в качестве начального звено
2. Тогда
механизм будет состоять из начального
звена 2,
обладающего
одной степенью свободы,
стойки 1
и звеньев,
образующих кинематическую цепь,
состоящую из звеньев 3,
4, 5 и 6.
Процесс
образования
этого механизма можно представить как
последовательное присоединение к
начальному звену 2
и к стойке
1 кинематической
цепи, состоящей из звеньев З
и 4.
Тогда получим
четырехзвенный механизм АВCD,
обладающий
одной степенью
свободы. Далее к
звену 4
механизма
AВСD
и стойке 1
присоединим
кинематическую цепь, состоящую из звена
5 и
ползуна 6.
Тогда получим
шестизвенный механизм, обладающий
также одной степенью свободы.
Нетрудно теперь
установить определенную закономерность
процесса образования механизма. В самом
деле, любой механизм имеет одно
неподвижное звено (стойку).
У механизма,
показанного на рис. З.1, стойкой будет
звено 1. далее,
механизм должен иметь число начальных
звеньев, равное числу его степеней
свободы. В
нашем случае механизм (рис. 3.1) обладает
одним начальным звеном 2,
так как
степень свободы механизма согласно
(3.1) равна W=1
Так как после присоединения звеньев
3, 4, 5 и
б число степеней свободы всего механизма
осталось равным W=1,
то, следовательно, кинематическая цепь,
состоящая из звеньев 3,
4, 5 и 6,
присоединенных к начальному звену 2
и стойке 1,
обладает
нулевой степенью свободы относительно
тех звеньев, к которым эта цепь
присоединяется. При последовательном
присоединении групп
необходимо
руководствоваться определенными
правилами. При образовании механизма
с одной степенью свободы первая группа
присоединяется свободными элементами
звеньев к начальному звену и к стойке.
Последующие группы могут присоединиться
к любым звеньям
полученного механизма только так, чтобы
звенья группы обладали
подвижностью
друг относительно
друга. Пусть,
например,мы
имеем
четырехзвенный механизм
АВСD
(рис. 3.2),
образованный
начальным
звеном 2,
стойкой 1
и группой,
состоящей из
звеньев 3 и
4. Следующая
группа, состоящая из звеньев 5
и 6,
может быть
присоединена
к любым двум разным звеньям механизма,
например к звеньям 3
и 4
(рис. 3.2), но
не к одному и тому же звену. Так, например,
если присоединить звенья 5
и 6
к одному и
тому же звену 3
(рис. 3.2). то
контур FEG’,
образованный
звеньями 3,
5 и 6, будет
жестким, т. е. будет фермой.Нетрудно
видеть, что
для того,
чтобы после
присоединения группы ее звенья имели
подвижность относительно тех звеньев,
к которым группа присоединена, необходимо,
чтобы замкнутый контур, образованный
звеньями группы и звеньями, к которым
она присоединится, был подвижным
контуром. Так, на
рис. 3.2 контур
GСFЕ
будет обладать
подвижностью. Нетрудно видеть, что для
того, чтобы
такой контур
обладал подвижностью, необходимо, чтобы
звенья контура входили бы не
менее чем
в четыре
кинематические
пары (пары F,
Е,G
и С на рис.
3.2).
6 Единый принцип образования механизмов по Ассуру. Согласно принципу, сформулированному Ассуром механизм может быть образован последовательным присоединением к одному или нескольким первичным механизмам (начальным звеньям) одной или нескольких кинематических цепей нулевой подвижности ( W = 0), причем каждая цепь должна быть подсоединена не менее чем к двум звеньям. Первичный механизм состоит из стойки и одного подвижного звена и обладает степенью подвижности W=3*1-2*1=1; Число первичных механизмов равно числу степеней подвижности всего механизма. Если от механизма отделить первичный механизм (начальное звено), то освободившаяся ведомая кинематическая цепь будет иметь степень подвижности равную нулю, если её присоединить к стойке освободившимися звеньями. W=3*3-2*4=1 W=3*1-2*1=1 W=3*2-2*3=0 Кинематическая цепь, имеющая степень подвижности равную нулю Механизм Начальное звено Группа
Если все кинематические пары 4 класса заменить парами 5 класса, то формула Чебышева примет вид:
W=
0 Тогда
и т. д. В соответствии с числом кинематических пар, входящих в замкнутый контур звеньев проводится классификация групп. В Разделять механизм на группы нужно, начиная с наиболее удаленной от начального звена. |
7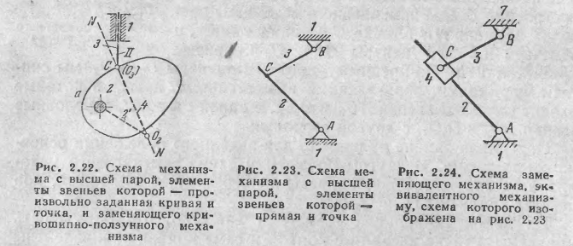
 )
Замена в
плоских механизмах высших пар низшими
(Рисунки мотреть в конспекте)При
изучении структуры и кинематики плоских
механизмов во многих случаях удобно
заменять высшие пары кинематическими
цепями или звеньями, входящими только
в низшие вращательные и поступательные
пары 5 класса. При этой замене должно
удовлетворяться условие, чтобы механизм,
полученный после такой замены, обладал
прежней степенью свободы и чтобы
сохранились относительные в рассматриваемом
положении движения всех его звеньев.
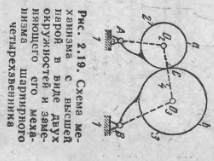
Рассмотрим трехзвенный механизм,
показанный на рис. 2.19. Механизм состоит
из двух подвижных звеньев 2
и 3,
входящих во
вращательные пары 5 класса А
и В
со стойкой
1 и
высшую пару С
4 класса,
элементы звеньев а и b
которой
представляют собою окружности радиусов
02С и
03С. Согласно
формуле (2.5) степень свободы механизма
будет = 1. W=3*n-2*P5-P4=3*2-2*2-1=1
Можно показать, что рассматриваемый
механизм может быть заменен эквивалентным
ему механизмом шарнирного четырехзвенника
А0203В. Высшая
нара 4 класса в точке С
заменяется
звеном 4,
входящим в
точках 02 и О3
во вращательные
пары 5 класса. Полученный в результате
замены механизм А0203B
называется
заменяющим
механизмом. Степень
свободы ‚W
заменяющего
механизма будет той же, что и у заданного
механизма. Имеем W=Зn—2р5=З*3—2*4=
1. Так как
элементы а и b
звеньев являются окружностями с центрами
в точках 02 и
О3, то
длина 0203
звена 4
оказывается постоянной. Точно так же
будут постоянными
и длины АО2
и ВО2
звеньев 2
и З. Заменяющий
механизм А0203В
эквивалентен
заданному и с точки зрения законов
движения звеньев2 и З.
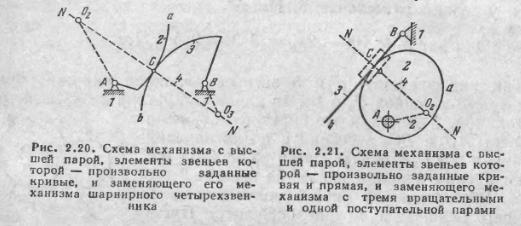
Рассмотренный
способ получения заменяющего механизма
можно обобщить. Пусть задан механизм
с высшей парой, элементы звеньев которой
представляют собой произвольно заданные
кривые а и b
(рис. 2.20). для
построения схемы заменяющего механизма
про водим
нормаль NN
в точке С
касания
кривых и отмечаем на ней центры 02 и О3
кривизны
кривых а и b.
По-прежнему
центры кривизны 02 и О3
мы считаем
шарнирами, образующими вращательные
пары, в которые входят условные звенья
АО2 и
0203, с
одной стороны, и условные звенья ВО3
и 0203, с другой
стороны. Описанная
замена правильна для заданного положения
основного механизма. В другом положении
схема заменяющего механизма останется
той же, размеры же его звеньев изменятся,
ибо центры кривизны 02 и О3
сместятся.
Из дифференциальной геометрии известно,
что окружность кривизны в точке касания
с кривой и сама кривая эквивалентны до
производных второго порядка включительно,
и поэтому заменяющий механизм эквивалентен
основному в такой же степени, т. е.
положения, скорости и ускорения
одноименных точек того и другого
механизма будут одинаковыми.Если один
из соприкасающихся элементов будет
представлять собой некоторую кривую,
а второй прямую b
(рис. 2.21), то центр крпвизны второго
профиля будет бесконечно удален.
Условное звено 4
в этом случае
будет входить в центре кривизны 02
элемента 2
во вращательную
пару 5 класса. Вторая вращательная пара,
в которую должно входить звено 3,
имеет ось
вращения бесконечно удаленной и
переходит в поступательную пару также
5 класса.
далее возможен
случай, когда один из соприкасающихся
элементов -- кривая а, а другой — точка
С (рис.
2.22). В этом
случае центр кривизны О
элемента С
совпадает
с самой точкой С
и поэтому
условное звено 4
должно
ВХОДИТЬ в две вращательные пары 5
класса — во
вращательную пару с осью, проходящей
через центр кривизны 02 криволинейного
элемента а, и во вращательную пару с
осью, проходящей через точку С.
В том
случае, когда одним элементом является
прямая АС, а
другим — точка С
(рис. 2.23),
замена сводится
к постановке условного звена 4, входящего
в одну поступательную и одну вращательную
пары. Ось вращательной пары и ось
движения поступательной пары должны
проходить через точку соприкосновения
С. Заменяющий
механизм показан на рис. 2.24. Таким
образом, любой плоский механизм с
высшими парами 4 класса может быть
заменен механизмом, в состав которого
входят только низшие кинематические
пары 5 класса.Если все высшие пары 4
класса в плоском механизме заменены
низшими парами, то структурная формула
(2.5) для заменяющего механизма получит
вид
W=3n-2P5
)
Замена в
плоских механизмах высших пар низшими
(Рисунки мотреть в конспекте)При
изучении структуры и кинематики плоских
механизмов во многих случаях удобно
заменять высшие пары кинематическими
цепями или звеньями, входящими только
в низшие вращательные и поступательные
пары 5 класса. При этой замене должно
удовлетворяться условие, чтобы механизм,
полученный после такой замены, обладал
прежней степенью свободы и чтобы
сохранились относительные в рассматриваемом
положении движения всех его звеньев.
Рассмотрим трехзвенный механизм,
показанный на рис. 2.19. Механизм состоит
из двух подвижных звеньев 2
и 3,
входящих во
вращательные пары 5 класса А
и В
со стойкой
1 и
высшую пару С
4 класса,
элементы звеньев а и b
которой
представляют собою окружности радиусов
02С и
03С. Согласно
формуле (2.5) степень свободы механизма
будет = 1. W=3*n-2*P5-P4=3*2-2*2-1=1
Можно показать, что рассматриваемый
механизм может быть заменен эквивалентным
ему механизмом шарнирного четырехзвенника
А0203В. Высшая
нара 4 класса в точке С
заменяется
звеном 4,
входящим в
точках 02 и О3
во вращательные
пары 5 класса. Полученный в результате
замены механизм А0203B
называется
заменяющим
механизмом. Степень
свободы ‚W
заменяющего
механизма будет той же, что и у заданного
механизма. Имеем W=Зn—2р5=З*3—2*4=
1. Так как
элементы а и b
звеньев являются окружностями с центрами
в точках 02 и
О3, то
длина 0203
звена 4
оказывается постоянной. Точно так же
будут постоянными
и длины АО2
и ВО2
звеньев 2
и З. Заменяющий
механизм А0203В
эквивалентен
заданному и с точки зрения законов
движения звеньев2 и З.
Рассмотренный
способ получения заменяющего механизма
можно обобщить. Пусть задан механизм
с высшей парой, элементы звеньев которой
представляют собой произвольно заданные
кривые а и b
(рис. 2.20). для
построения схемы заменяющего механизма
про водим
нормаль NN
в точке С
касания
кривых и отмечаем на ней центры 02 и О3
кривизны
кривых а и b.
По-прежнему
центры кривизны 02 и О3
мы считаем
шарнирами, образующими вращательные
пары, в которые входят условные звенья
АО2 и
0203, с
одной стороны, и условные звенья ВО3
и 0203, с другой
стороны. Описанная
замена правильна для заданного положения
основного механизма. В другом положении
схема заменяющего механизма останется
той же, размеры же его звеньев изменятся,
ибо центры кривизны 02 и О3
сместятся.
Из дифференциальной геометрии известно,
что окружность кривизны в точке касания
с кривой и сама кривая эквивалентны до
производных второго порядка включительно,
и поэтому заменяющий механизм эквивалентен
основному в такой же степени, т. е.
положения, скорости и ускорения
одноименных точек того и другого
механизма будут одинаковыми.Если один
из соприкасающихся элементов будет
представлять собой некоторую кривую,
а второй прямую b
(рис. 2.21), то центр крпвизны второго
профиля будет бесконечно удален.
Условное звено 4
в этом случае
будет входить в центре кривизны 02
элемента 2
во вращательную
пару 5 класса. Вторая вращательная пара,
в которую должно входить звено 3,
имеет ось
вращения бесконечно удаленной и
переходит в поступательную пару также
5 класса.
далее возможен
случай, когда один из соприкасающихся
элементов -- кривая а, а другой — точка
С (рис.
2.22). В этом
случае центр кривизны О
элемента С
совпадает
с самой точкой С
и поэтому
условное звено 4
должно
ВХОДИТЬ в две вращательные пары 5
класса — во
вращательную пару с осью, проходящей
через центр кривизны 02 криволинейного
элемента а, и во вращательную пару с
осью, проходящей через точку С.
В том
случае, когда одним элементом является
прямая АС, а
другим — точка С
(рис. 2.23),
замена сводится
к постановке условного звена 4, входящего
в одну поступательную и одну вращательную
пары. Ось вращательной пары и ось
движения поступательной пары должны
проходить через точку соприкосновения
С. Заменяющий
механизм показан на рис. 2.24. Таким
образом, любой плоский механизм с
высшими парами 4 класса может быть
заменен механизмом, в состав которого
входят только низшие кинематические
пары 5 класса.Если все высшие пары 4
класса в плоском механизме заменены
низшими парами, то структурная формула
(2.5) для заменяющего механизма получит
вид
W=3n-2P5

 получила
название структурной группы Ассура.
получила
название структурной группы Ассура.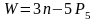 ;Приравняем
к нулю левую часть формулы, т. к. у
группы Ассура
;Приравняем
к нулю левую часть формулы, т. к. у
группы Ассура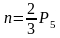
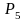 и n
и n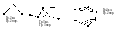 соответствии с числом не присоединенных
кинематических пар определяют порядок
группы. Класс и порядок механизмов
определяется наивысшим классом и
порядком группы,
входящей в его состав.
соответствии с числом не присоединенных
кинематических пар определяют порядок
группы. Класс и порядок механизмов
определяется наивысшим классом и
порядком группы,
входящей в его состав.