4. Энтропия источника сообщения. Энтропия Шеннона & 5. Энтропия Хартли

Информационной характеристикой алфавита (источника сообщений на основе этого алфавита) является энтропия. Этот термин применительно к техническим системам был введен Шенноном и Хартли.

Энтропию алфавита по Шеннону рассчитывают по следующей формуле:

(2.1)

Заметим, что _.

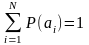С физической точки зрения энтропия показывает, какое количество информации приходится в среднем на один символ алфавита.

Частным случаем энтропии Шеннона является энтропия Хартли. Дополнительным условием при этом является то, что все вероятности одинаковы и постоянны для всех символов алфавита. С учетом этого формулу (2.1) можно преобразовать к следующему виду:

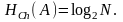
Например, энтропия Хартли для латинского (английского) алфавита составляет 4,7 бит.

Если подсчитать энтропию Шеннона и энтропию Хартли для одного и того же алфавита, то они окажутся не равными. Это несовпадение указывает на избыточность любого алфавита (при ).

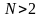Сообщение которое состоит из 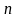символов, должно характеризоваться определенным количеством информации :

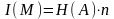. (2.2)

Нетрудно предположить и просто убедиться, что количество информации в сообщении, подсчитанное по Шеннону, не равно количеству информации, подсчитанному по Хартли. На основе этого парадокса строятся и функционируют все современные системы сжатия (компрессии) информации.

6. Двоичный канал передачи информации

Как было подчеркнуто выше, двоичный канал передачи информации является дискретным. Он основан на алфавите, состоящем из двух символов (0 и 1) –  . Используя (2.1), вычислим энтропию этого алфавита:

. (2.3)

К примеру, полагая, что сообщение состоит только из единиц ( ) и имеет длину : , т. е. вероятность того, что произвольный символ равен единице, составляет единицу (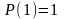 ), тогда для . Фактически здесь имеет место использование моноалфавита – алфавита, состоящего из одного символа.

Если в этом случае подставить в (2.3) соответствующие значения, то получим, что энтропия моноалфавита равна 0 бит, количество информации в сообщении из единиц (либо из нулей) также составляет 0 бит. Этот практический результат поясняет физический смысл понятия информации в теории Шеннона: информацией является лишь такое сообщение, которое снимает некоторую неопределенность, т. е. содержит новые для получателя данные. Если априори известно, что сообщение будет состоять из набора одинаковых символов, то для получателя сообщения оно никакой неопределенности не содержит.

Если для бинарного алфавита вероятность появления в произвольном сообщении одного из этих символов стремится к нулю (или равна ему), то энтропия такого алфавита также будет стремиться к нулю или равняться ему.

Между этими точками значение функции (энтропии) должно пройти через максимум (так как энтропия не может быть отрицательной). Для нахождения этого максимального значения надо найти производную:

Таким образом, энтропия бинарного алфавита принимает максимальное значение, равное 1 бит, при условии равновероятного появления каждого символа алфавита в сообщении (рис. 2.2).

Рис. 2.2. Качественная характеристика энтропии бинарного алфавита

при различных значениях вероятностей появления символов в сообщении

Интересным представляется оценка количества информации в сообщении, выполненная на основе различных подходов.

Пример 2.1. Анализируем сообщение «We are happy» (пробелы не учитываем). Если принять, что энтропия английского алфавита, вычисленная по Шеннону, составляет 4,2 бит (примерно), то в анализируемом сообщении содержится 42 бита информации: бита.

С другой стороны, предполагая, что сообщение переведено в ASCII коды (один символ алфавита заменяется соответствующим байтом двоичных символов), и допустив, что 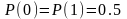, получаем бит.

Данный пример является свидетельством и подтверждением избыточности не только алфавита, но и сообщений, сформированных и обрабатываемых в компьютерных системах, т. е. любые сообщения характеризуются информационной избыточностью, что позволяет сжимать их без потери информации.