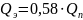7.1.3 Расчет сложных трубопроводов

7.1.3.1 Последовательное соединения простых трубопроводов

При таком соединении в единый трубопровод входит несколько труб различной длины, разного диаметра и содержащих различные местные сопротивления.

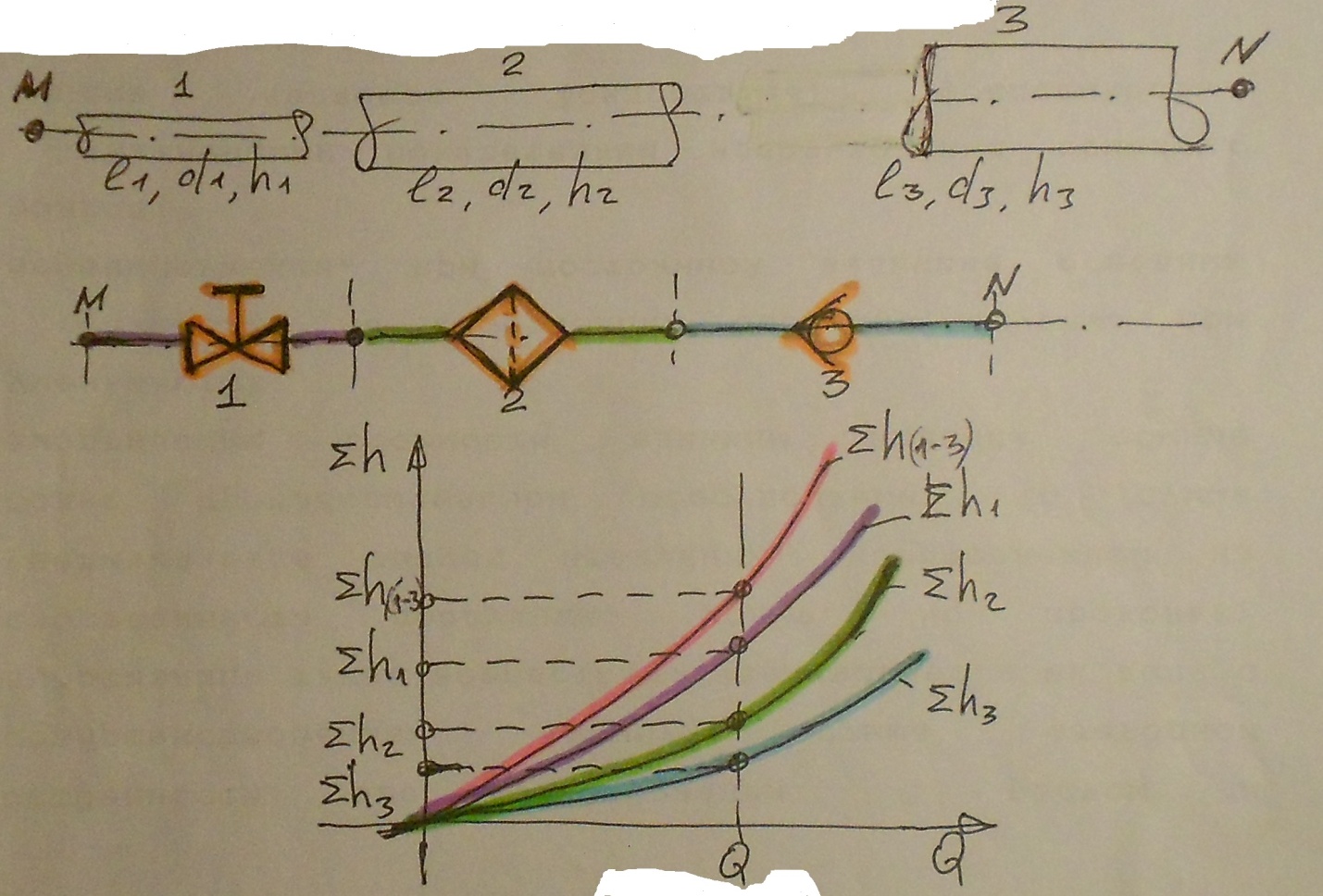
Рис. 7.1.7 Схема сложного трубопровода и график потребного напора

)

∑h =∑ +∑ +∑

∑ = ∙

∑ = ∙

∑ = ∙

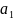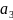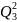
Так как = Q, то ∑h = ( )∙

где

a – обобщенный коэффициент сопротивления

При подаче жидкости по последовательно соединенных простым трубопроводам от точки М до точки N расход жидкости Q во всех последовательно соединенных трубопроводах 1,2 и 3 будет одинаковый, а полная потеря напора между точками M и N равна сумме потерь напора во всех последовательно соединенных трубах.

Таким образом, для последовательного соединения трубопроводов расход жидкости на входе в сложный трубопровод равен расходам жидкости в каждом простом трубопроводе, а потеря напора в трубопроводе равна сумме потерь напоров на каждом простом участке трубопровода:

∑ =∑ +∑ +∑

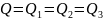
Эти уравнения определяют правила построения характеристик последовательного соединения труб. Если известны характеристики каждого трубопровода, то по них можно построить характеристику всего последовательного соединения простых трубопроводов M-N.

7.1.3.2 Параллельное соединения простых трубопроводов

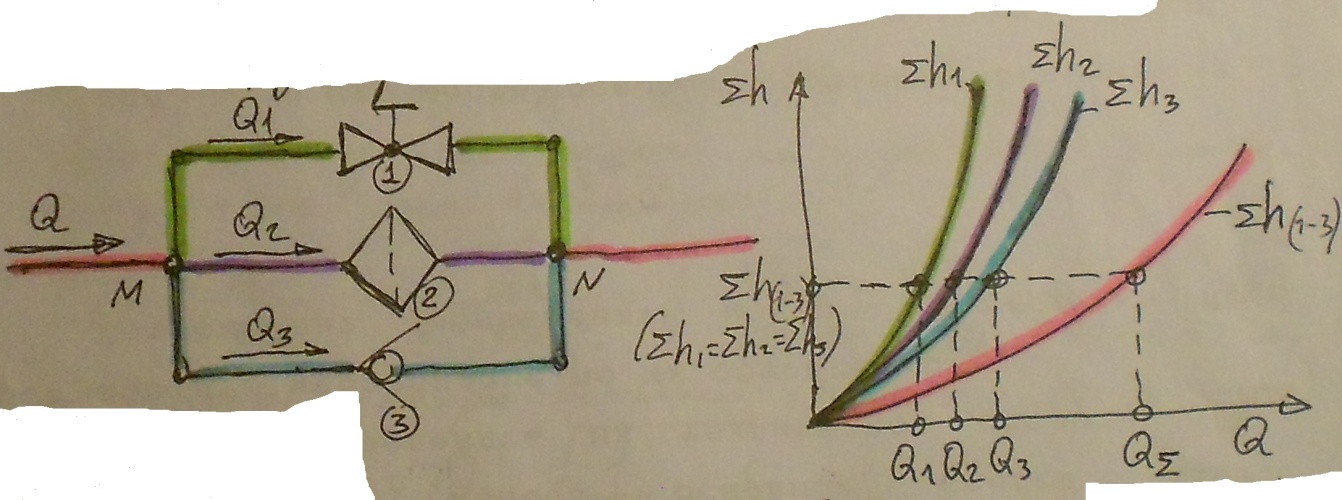
Рис. 7.1.8 Схема сложного трубопровода и график потребного напора

( )

(∑ =∑ =∑ =∑ )

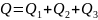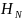Обозначим полные напоры в точке М и точке N ( ) и ( ), расход в основной магистрали (до разветвления и после слияния) – через Q, а в параллельных трубопроводах , , 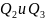а суммарные напоры в этих трубопроводах через ∑ , ∑ , ∑

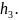
Расход жидкости в основной магистрали равен сумме расходов в каждой параллельной ветви сложного трубопровода:

,

а потери напора в основной магистрали равны:

∑ =∑ =∑ =∑

Таким образом, в параллельных трубопроводах потери напора равны между собой, а расход жидкости до разветвления равен суме расходов жидкости в каждой параллельной ветви.

Потребный напор в точке М можно определить из уравнения:

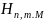= = ∆y + + = ∆y + + = ∆y + +

Так как уравнение неразрывности потока при параллельном соединении имеет вид:

,

то потери напора в каждом трубопроводе будут составлять:

∑ = ∙ ;

∑ = ∙ ;

∑ = ∙ .

Потери напора в каждом простом трубопроводе, а также общие потери напора в сложном трубопроводе при параллельном соединении равны разности полных напоров в сечение M и N.

- = ∑ =∑ =∑ ∑

Общий расход жидкости по трубопроводу можно определить по формуле:

Q = + + = ( + + )∙

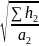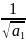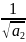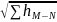
тогда потери напора можно определить по формуле:

∑

Таким образом, сопротивление сложного трубопровода, состоящего из нескольких простых трубопроводов, соединенных параллельно, уменьшается и в общем случае равно:

a =

7.1.3.3 Трубопровод с путевым расходом жидкости

Трубопроводом с путевым расходом жидкости называется такой трубопровод, из ко-торого жидкость расходуется по его длине. При большом числе пунктов расхода жидкос-ти можно считать, что отбор жидкости осуществляется равномерно с интенсивностью:

q =

Рассмотрим общий случай, когда в трубопроводе кроме равномерного путевого расхода 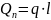жидкости , имеется также транзитный расход жидкости 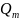. Таким образом общий расход жидкости равен сумме и :

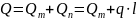
Выделим на некотором расстоянии от начала трубопровода (х) бесконечно малый участок длиной (dx). Расход на этом участке считается условно постоянным и равным:

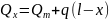
Рис. 7.1.9 Схема трубопровода с путевым расходом жидкости

Потери напора на этом участке будут равны:

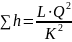
или через дифференциал:

∑dh=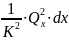

Приняв, что по длине трубопровода коэффициент 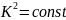, тогда проинтегриро-вав дифференциальное уравнение потерь напора по всей длине трубопровода получим:

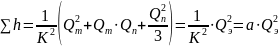
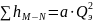
где

- обобщенный параметр сопротивления трубопровода;

- эквивалентный расход жидкости в конце трубопро-вода.

Если транзитный расход в трубопроводе отсутствует ( ), то эквивалентный расход равен: