14

Тема 7: гидравлический расчет трубопроводов.

ПОСТРОЕНИЕ ИХ ХАРАКТЕРИСТИК

ЛЕКЦИЯ 7.1: ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ

План:

7.1.1. Классификация трубопроводов

7.1.2. Расчет простых трубопроводов

7.1.3. Расчет сложных трубопроводов

7.1.1 Классификация трубопроводов

При расчетах напорных трубопроводов основными задачами расчета является:

• определение пропускной способности трубопровода (определение расхода жидкости);

• определение потерь напора на отдельных участках или всей длине трубо-провода;

• определение геометрических параметров трубопровода при заданных рас-хода жидкости и потерях напора.

С гидравлической точки зрения трубопроводы разделяются на:

• короткие [h(м)˃5-10%·h(l)];

• длинные [h(м)≤ 5-10%·h(l)].

К коротким относятся такие трубопроводы, в которых потери в местных сопротивле-ниях составляют более 5-10% от потерь напора на прямых участках трубопровода. При расчете таких трубопроводов учитываются потери напора в местных сопротивлениях.

К длинным относятся такие трубопроводы, в которых потери напора по длине нас-только превышают местные потери напора, что ими можно пренебречь (такие потери меньше или равны 5-10% от потерь напора по длине трубопровола).

В зависимости от соединения отдельных участков трубопроводов и их геометричес-ких параметров трубопроводы условно разделяются на:

• простые;

• сложные.

Простыми называются последовательно соединенные трубопроводы одного диамет-ра и не имеющие по длине боковых ответвлений.

Сложными являются трубопроводы состоящие из нескольких простых трубопрово-дов, соединенных: последовательно, параллельно или разветвлено определенным спосо-бом.

Сложные трубопроводы условно разделяются на:

• тупиковые (незамкнутые);

• кольцевые (замкнутые).

В зависимости от характера движения жидкости трубопроводы разделяются на:

• насосные (напорные);

• самотечные (ненапорные).

Гидравлические расчеты трубопроводов осуществляются на основе теоретических основ гидравлики, которые включают в себя:

• уравнение неразрывности (уравнение Л. Эйлера);

• уравнение баланса энергии потока (уравнение Д.Бернулли);

• формула расчета числа Рейнольдса (Re);

• формулы расчета коэффициента Дарси (λ);

• формул расчета потерь напора по длине трубопровода (h(l)) и местных сопротивлений (h(м)).

7.1.2 Расчет простых трубопроводов

Жидкость по трубопроводу может двигаться вследствие разности энергий на входе в трубопровод и на выходе из него.

Перепад энергий может создаваться разными способами:

• подачей жидкости на входе в трубопровод насосом;

• разностью давлений между входом и выходом в трубопроводе;

• разностью уровней жидкости на входе и выходе из трубопровода.

7.1.2.1 Гидравлический расчет простого трубопровода

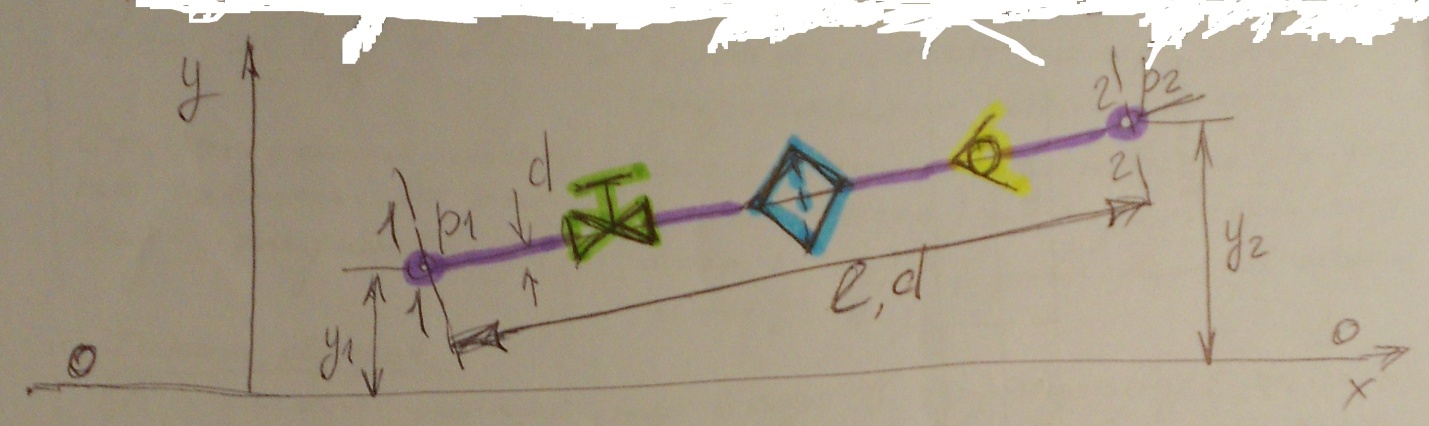
Рис. 7.1.1 Схема простого трубопровода

Рассмотрим простой короткий трубопровод, имеющий постоянный диаметр и распо-ложенный произвольно в пространстве.

Трубопровод имеет длину (l), диаметр (d) и содержит ряд местных сопротивлений:

• вентиль;

• фильтр;

• обратный клапан.

На входе в трубопровод в сечении «1-1»:

• геометрическая высота равна – у₁;

• избыточное давление – р₁.

На выходе из трубопровода в сечение «2-2»:

• геометрическая высота – у₂;

• избыточное давление – р₂.

Так как диаметр трубопровода одинаков на всем его протяжении, то и скорость по-тока по сечениям одинакова V₁=V₂, при этом и коэффициенты Кориолиса по сечениям трубопровода также будут одинаковыми (α₁=α₂).

Составим уравнение Д.Бернулли для данного трубопровода:

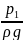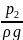у₁+ + = y₂ + + +∑ h_1-2

С учетом принятых упрощений простого трубопровода: d₁=d₂; S₁=S₂; V₁=V₂; α₁=α₂ уравнение можно упростить:

у₁+ = = y₂ + +∑ h_1-2

Определим величину потребного напора на входе в трубопровод:

H_п = = (y₂-y₁) + + ∑ h_1-2 = H_ст +∑ h_1-2

Отсюда:

H_ст = ∆y + - статический напора, который представляет собой сумму геометрического напора (разность высот) и пьезометрического напора (давления в сечении «2-2»). Статический напор не зависит от расхода жидкости – Q.

Таким образом, полный напор на входе в трубопровод (Н_п) включает в себя:

• геометрический напор (у₂-у₁);

• пьезометрический напор ( );

• сумму потерь напора в трубопроводе между сечениями «1-1» и «2-2»- ∑ h_1-2

Н_п = ∆у + + ∑ h_(1-2)

Пьезометрический напор (или высоту) в сечении «1-1» называют потребным напо-ром и обозначают (Н_п).

Если по условиям расчета пьезометрический напор задан, то его называют распола-гаемым напором (Н_расп).

Составим уравнение суммарных потерь напора в трубопроводе:

∑h_(1-2) = h(l) + h(м) = 𝜆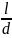 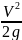+ ∑ζ_м,i = (𝜆 + ∑ζ_м,i)∙

Скорость течения жидкости можно выразить через расход:

V =

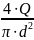
Подставим формулу скорости в уравнение потерь напора и после необходимых пре-образований получим выражения потерь напора через расход:

∑h_(1-2) =( _*∑l + _*∑ζ)_* Q²

Выражение в скобках называется сопротивлением трубопровода и обозначается буквой (а).

При турбулентном режиме течения жидкости и гидравлически шероховатых трубах условно считается, что а = соnst. Тогда уравнение потерь напора можно записать в виде:

∑h_(1-2) = а∙Q² или

H_п = H_ст + а∙Q² – потребный напор на входе в трубопровод

Выполним некоторые преобразования и обозначим:

= h(l);

где

h(l) – единичное сопротивление трения по длине;

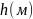- единичное местное сопротивление.

Тогда потребный напор в трубопроводе можно определить по уравнению:

H_п = [h(l)∙∑l +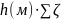 ] Q²

Значения величин h(l) и (обобщенных параметров трубопровода) выбираются из таблиц по гидравлике.

Потребный напор в длинных трубопроводах можно определить по формуле:

H_п = h(l)∙L∙Q²

где

L = (1,05…1,1) l – расчетная длина трубопровода

В справочниках по гидравлическим расчетам можно встретить расчетную формулу другого вида:

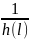= К²

где

К – обобщенный параметр трубопровода, учитывающий сопротивление трения по длине трубопровода. Тогда потребный напор можно определить по формуле:

H_п =