6. Эволюционно-стабильная стратегия

85

Разновидностью повторяющихся игр являются ситуации, когда индивид многократно попадает в определенную ситуацию выбора, но его контрагент не постоянен, а в каждом периоде индивид взаимодействует с новым визави. Поэтому вероятность выбора контрагентом той или иной стратегии будет зависеть не столько от конфигурации смешанной стратегии, сколько от пред­почтений каждого из контрагентов. В частности, предполагается, что из общего числа N потенциальных контрагентов п (n/N%) всегда выбирают стратегию А, а т (m/N%) — стратегию Б. Тем самым создаются предпосылки для достижения нового типа равно­весия, эволюционно-стабильных стратегий. Эволюционно-стабильной (ESS — Evolutionarily Stable Strategy) становится та стратегия, при которой если все члены определенной популяции используют се, то никакая альтернативная стратегия не может ее вытеснить посредством механизма естественного отбора¹⁰. Рассмотрим в качестве примера простейший вариант проблемы координации: разъезд на узкой дороге двух автомобилей (ситуация близка по некоторым параметрам и к модели I, и к модели IV). Предполага­ется, что в данной местности лево- и правосторонний стандарты движения равноправны (или же Правила дорожного движения просто не всегда выполняются)¹¹. Автомобилю А движутся на­встречу несколько автомобилей, с которыми ему нужно разъехаться. Гели оба автомобиля принимают влево, въезжая на левую обочину но ходу движения, то они разъезжаются без проблем. То же самое происходит, если оба автомобиля принимают вправо. Когда же один автомобиль принимает вправо, а второй — влево и наоборот, ю разъехаться они не смогут:

Итак, автомобилисту А известен приблизительный процент автомобилистов Б, систематически принимающих влево (Р), и процент автомобилистов Б, принимающих вправо (1 — Р). Усло­вие для того, чтобы стратегия «принять вправо» стала для автомо­билиста А эволюционно-стабильнои, формулируется следующим образом: ЕЬ (вправо) > ££/(влево), или 0Р+ 1(1 - Р)(1Р+ 0(1 - Р), откуда Р> 1/2. Таким образом, при превышении доли автомо­билистов во встречном потоке, принимающих вправо, уровня 50% эволюционно-стабильной стратегией становится «принять вправо» — сворачивать на правую обочину при каждом разъезде.

Эволюционно-стабильная стратегия — такая стратегия, - что если ее использует большинство индивидов, то никакая альтернативная стратегий не может ее вытеснить посредст­вом механизма естественного отбора, даже если последняя более эффективна по Парето.

В общем виде требования к эволюционно-стабильной страте­гии записываются следующим образом. Стратегия I, использу­емая контрагентами с вероятностью р, является эволюционно-стабильнои для игрока тогда и только тогда, когда выполняются следующие условия: EU{\,p)> EU(J, р), что тождественно pU(l, I) + (1 -p)U(I, J)>pU(J, I) + (1 -p)U(J, J). Из чего следует:

• U(I,I)> U{J,I) или

• U(I, I) = U(J, I) и U(I, J) > U(J, J),

где — U (I, /) выигрыш игрока при выборе стратегии /, если контр­агент выбирает стратегию /; £/(/,/) — выигрыш игрока при выборе стратегии /, если контрагент выбирает стратегию /, и т. д.

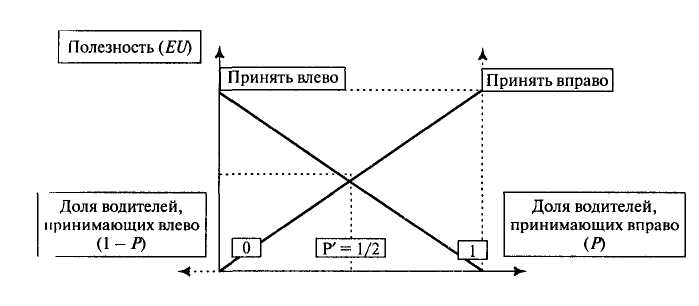
Можно представить эти условия и в графической форме. Отло­жим по вертикальной оси ожидаемую полезность выбора той или иной стратегии, а по горизонтальной — долю индивидов в общей популяции игроков, выбирающих обе стратегии. Тогда мы полу­чим следующий график (значения взяты из модели разъезда двух автомобилей), изображенный на рис. 6.1.

Из рисунка следует, что и «принять влево», и «принять вправо» имеют равные шансы на то, чтобы стать эволюционно-стабильнои стратегией до тех пор, пока ни одна из них не охватила больше половины «популяции» водителей. Если же стратегия перешагивает этот рубеж, то она постепенно, но неизбежно вытеснит другую стратегию и охватит всю популяцию водителей. Дело в том, что,

86

если стратегия перешагивает рубеж 50%, для любого водителя становится выгодным использовать ее в маневрах, что, в свою оче­редь, еще больше увеличивает привлекательность данной стратегии для остальных водителей. В строгой форме данное утверждение Будет выглядеть следующим образом: dp/dt = G [EU(I, р) — EU(J, p)], (,">0.

Главным результатом анализа повторяющихся игр является увеличение числа точек равновесия и решение на этой основе про­блем координации, кооперации, совместимости и справедливости. Даже в дилемме заключенных, как мы уже упоминали в предыдущей лекции, переход к повторяющемуся взаимодействию позволяет достичь оптимального по Парето результата («отрицать вину»), не выходя за рамки нормы рациональности и запрета на обмен ин­формацией между игроками. Именно в этом смысл «всеобщей юоремы» (folk theorem): любой исход, устраивающий индивида индивидуально, может стать при переходе к структуре повторя­ющейся игры равновесным¹³. В ситуации дилеммы заключенных равновесным исходом при определенных условиях может стать и простая стратегия «не признавать», и множество смешанных стратегий. В числе смешанных и эволюционных стратегий, помимо I it for Tat («зуб за зуб»), отметим следующие: Tit-For-Two-Tats — начинать с отрицания вины и признавать вину, только если в два предшествующих периода кряду контрагент признавал вину; I )OWING — стратегия, исходящая из предположения о равновероятном использовании контрагентом стратегий «отрицать вину» и «признавать» в самом начале игры. Далее каждое отрицание вины со стороны контрагента поощряется, а каждое признание — наказывается выбором стратегии «признавать вину» в следующий период; TESTER — начинать с признания вины, и если контрагент тоже признает вину, то в следующем периоде отрицать вину (т. е. извиниться) и далее использовать стратегию «зуб за зуб» — Tit for Tat.

Выводы. Подведем общие итоги обзора теории игр и вари­антов ее использования в институциональном анализе. Главный аргумент в пользу того, чтобы строить модели институтов с помощью теории игр, заключается в интересе теории игр к ситуациям взаимо­зависимости действий индивидов, проблемам координации и согласования действий. Ведь именно институты призваны решить эти проблемы. С позиции теории игр функцию института можно определить как создание предпосылок (структурных, когнитив­ных, организационных) для фиксации одного из исходов игры в качестве равновесного. Эта задача особенно актуальна, если равно­весие по Нэшу отсутствует или оно не единственно. Достижение равновесия с помощью институтов подразумевает:

• увеличение числа точек равновесия через формирование сме­шанных и эволюционных стратегий;

• формирование репутации игроков, в которой фиксируется вся информация о его поведении в прошлом;

• задание «удовлетворительных» критериев выбора альтернатив;

• выбор единственного равновесия из нескольких равновесных исходов с помощью соглашений и «фокальных точек»;

• задание критериев выбора альтернатив на основе ценностей; изменение структуры предпочтений индивида.