3) Теория графов.

Теория графов предоставляет словарь для обозначения многих особенностей социальных структур, а также набор простых концепций, с помощью которых можно эти особенности оха­рактеризовать качественно и оценить количественно. Используя теоремы о свойствах графов, можно определять свойства социальных структур

Отношения между акторами могут быть как ненаправленными (например, «жить по со­седству»), так и направленными (например, импорт товара из одной страны в другую). Соот­ветственно для анализа первых применяются ненаправленные, или неориентированные, гра­фы, а для анализа последних — направленные, или ориентированные.

Неориентированные графы: основные понятия

Граф G= (N,Z) — это совокупность двух конечных множеств: множества точек N= {n ,, ...,n_g}, кото­рые называются вершинами, и множества пар вершин Z= {l₁,...,l_z}, которые называются ребрами.

Граф изображается точками на плоскости и линиями 1_к = {п_р п), соединяющими эти точ­ки. На рис. 3.6а показан граф, который имеет пять вершин и шесть ребер, а на рис. 3.6b — граф, который имеет четыре вершины и четыре ребра.

Ребра, имеющие одинаковые концевые вер­шины, называются параллельными. Ребро, кон­цевые вершины которого совпадают, называется петлей. На рис. 3.6а /₄ и /₅ — параллельные ребра, а /₂ — петля. Вершина и ребро называются инцидент­ными друг другу, если вершина является для этого ребра концевой точкой. На рис. 3.6а вершина п₃ и ребро 1_Л инцидентны друг другу.

Примеры графа

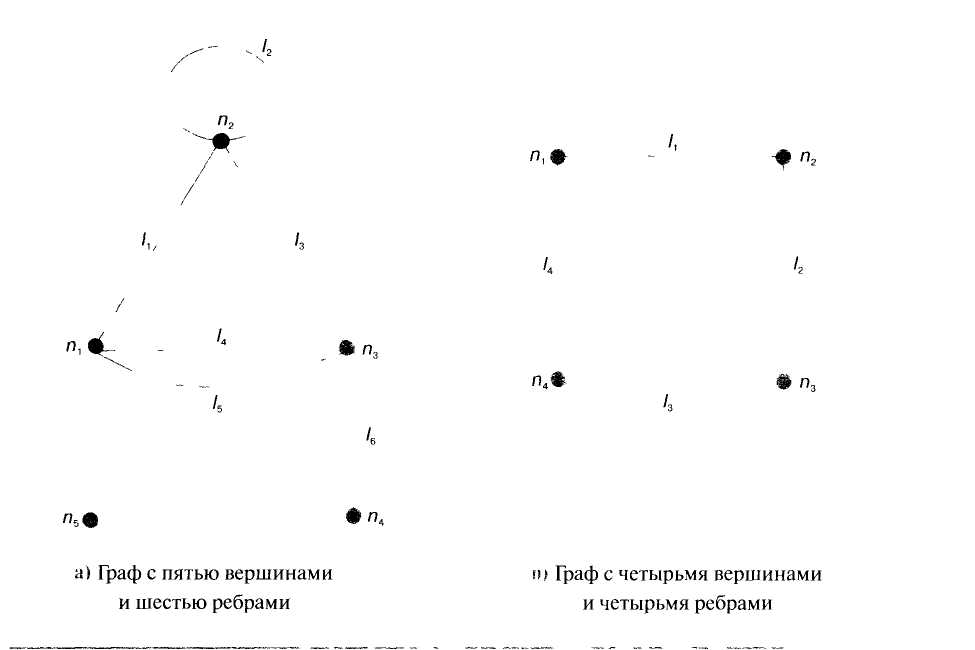
Две вершины, являющиеся концевыми для некоторого ребра, называются смежными вершинами. Два ребра, инцидентные одной и той же вершине, называются смежными ребрами. На рис. 3.6а n_1, п₂ — смежные вершины, а l₁,, l₄ — смежные ребра.

Степень вершины

Под степенью п-й вершины d(n) понимается число ребер, инцидентных этой вершине. Вер­шина степени 1 называется висячей. Вершина степени 0 называется изолированной. На рис. 3.6а степень «,-й вершины d(n_t) = 3, «₄ — висячая вершина, п₅ — изолированная.

В некоторых случаях важно определить среднюю степень вершин d для совокупности всех вершин графа. Для этого используют статистику:

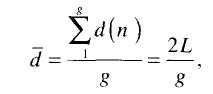
где L — общее число ребер графа,

g — общее число вершин графа

Граф G называется полным, если любые две его вершины соединены ребром и он не содержит параллельных ребер

Дополнением графа G называется граф с теми же вершинами, что и граф G, и содержащий только те ребра, которые нужно добавить к графу G, чтобы получился полный граф.

Циклом называется путь, начальная и конечная вершины которого совпадают. На рис. 3.6а ре­бра (l₁, l₃, l₄) образуют цикл.

Маршрутом между вершинами п_i и п_j графе называется последовательность ребер, ведущая от некоторой начальной вершины п₁ к конечной вершине п. Путем называется маршрут, не содер­жащий циклов. Дистанцией между двумя ребрами называется кратчайший путь между ними.

Связность графа

Граф G называется связным, если для любых двух его вершин существует путь, их соединяющий. В противном случае граф G называется несвязным. На рис. 3.8 представлен несвязный граф

Несвязный граф

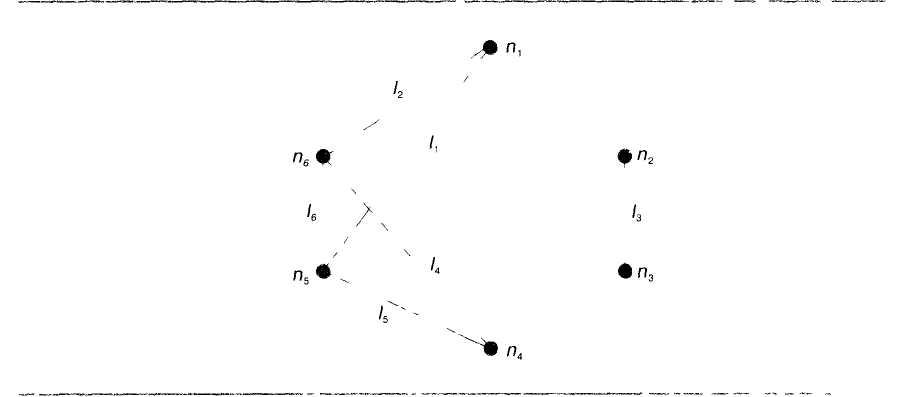
Любой несвязный граф является совокупностью таких связных графов, которые облада­ют следующим свойством: никакая вершина одного из них не связана путем ни с какой верши­ной другого. Каждый из этих графов называется компонентой графа G. В данном примере граф состоит из двух связных компонентов.

Ребро а называется мостом графа G, если граф, получив­шийся из G после удаления ребра а (такой граф обозна­чается G\ а), содержит больше компонент, чем граф G. Ребро а графа G является мостом тогда и только тогда, когда а не принадлежит ни одному циклу.

Плотность графа характеризуется коэффициентом плотности А — отношением числа ребер (L) в анализируемом графе к числу ребер в полном графе с тем же числом вершин (g):

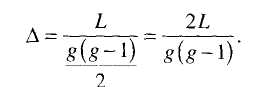
Коэффициент плотности варьируется в промежутке от 0 до 1, 0 ≤ Δ ≤ 1. Единичная плотность соответствует полному графу, нулевая — графу, в котором все вершины изолированные.

Частным случаем графов являются деревья. Они характеризуются тем, что содержат минималь­ное число ребер, необходимое для связности.

При этом

• любое ребро дерева представляет собой мост,

• l = g-1;

• существует только один путь между любыми двумя вершинами.

Ориентированные графы: основные понятия

Если рассматривается множество упорядоченных пар 1_к = (n_i, п_j) из множества точек N={n₁ ., п_g }, и на каждом ребре из множества Z= { l₁,...,l_z } задается направление, то граф G_d = (N,Z) называется ориентированным.. Если же на каждом ребре из множества Z= {l₁,...,l_z } направле­ние не задается, то граф G = (N, Z) называется неориентированным графом, или просто графом.

Примеры ориентированного графа

В ориентированном графе для каждой вершины различаются входящие и исходящие ребра. По­этому для характеристики отношений, связанных с конкретной вершиной, используют два по­казателя:

• степень захода d_m, которая равна числу ребер, входящих в вершину; и

• степень исхода d_oul, которая равна числу ребер, исходящих из вершины.

Плотность ориентированного графа характеризуется коэффициентом плотности Δ:

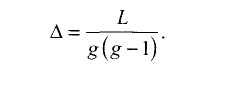
Матричное представление графов

Матрицы — альтернативная форма представления и суммирования информации о социаль­ных сетях. Такой способ в ряде случаев удобнее, чем графический.

Рассмотрим квадратную матрицу Х размерности пхп, где п — количество акторов в груп­пе. Зададим элементы этой матрицы следующим образом:

х = 1, если между акторами i и j существует связь,

x_v = 0, если между акторами i и j связь отсутствует.

Данная матрица содержит в себе полную информацию о связях акторов в группе. Так, матрица, описывающая граф на рис. 3.10b, имеет вид

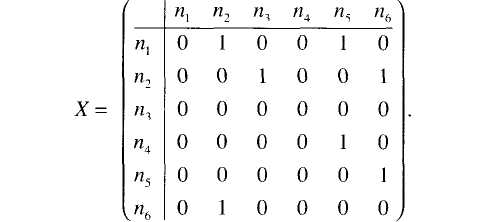
Заметим, что для ненаправленного графа матрица симметрична.

С помощью матричного представления графов можно, пользуясь простейшими опера­циями матричной алгебры, определять важные свойства этих графов.