4.2.1.3. Модель Ромера

Подход, представленный Ромером в его публикации 1986 года, находит отражение идеи модели Рамсея-Касс-Купмана, но он значительно отличается от него в двух очень важных аспектах. Первый аспект состоит в том, что модель сохраняет возрастающую отдачу от масштаба. Второй аспект: в модели предполагается, что важнейшим фактором экономического роста являются технологические изменения, которые происходят благодаря целенаправленной деятельности людей; дальнейшее использование созданных технологий не требует дополнительных затрат со стороны производителя.

Ромер предполагает, что амортизация уменьшает процесс накопления капитала. Поэтому, изменение акционерного капитала в каждой фирме j в период t dk_t,j/d_t и равняется инвестициям i_t,j фирм j в период t. Агрегируя все фирмы, совокупные инвестиции даны как сумма за все i_t,j:

Поскольку амортизация не считается, то совокупный запас капитала является суммой всех прошлых инвестиций. Затруднение модели Ромера в том, что акционерный капитал равняется акциям накопленного знания. В то время как это "сырой" путь к эндогинизированию знания, используя аргумент предыдущей главы, знание может быть включено во все товары. Беря этот аргумент на шаг вперед, Ромер подразумевает, что знание включено во все инвестиции. Поэтому, благоразумно принять то, что сумма всего знания, сгенерированного до времени t H_t, равняется акциям всех инвестиций, когда-либо сделанных в момент t и поэтому:

Включив в уравнение технологический прогресс, Ромер вводит отношение между уровнем технологического прогресса В и суммой накопленных знаний Ht:

Описывая производственный процесс через производственную функцию типа Кобб-Дугласа, это считается следующим образом как в агрегате, также и по фирме и при расчете на душу населения:

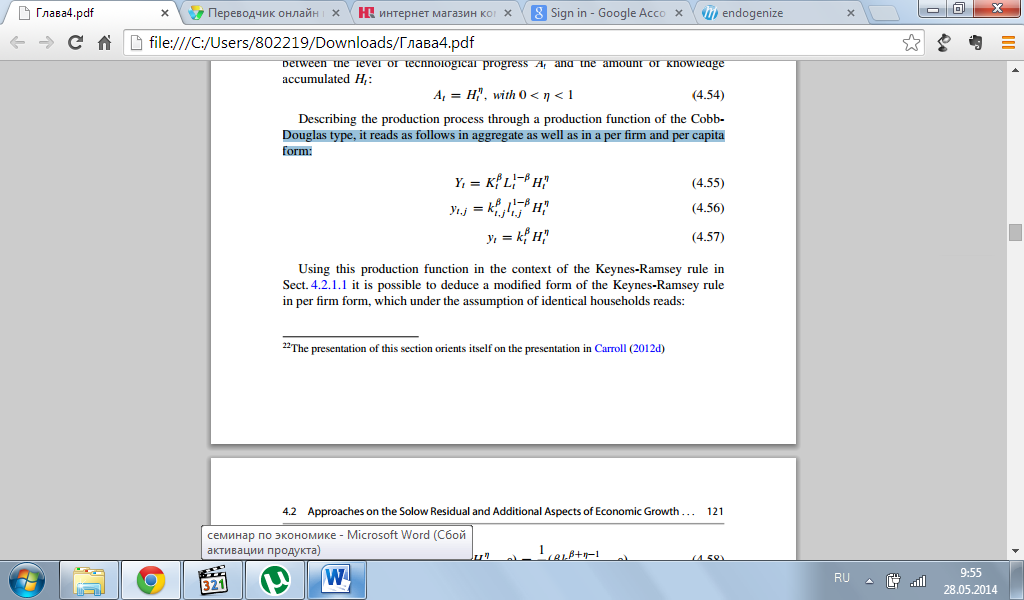
При помощи этой производственной функции в контексте закона Кейнса-Рэмси в разделе 4.2.1.1 возможно вывести форму модернизированного закона Кейнса-Рэмси для фирмы, которая при условии идентичных домашних хозяйств читается:

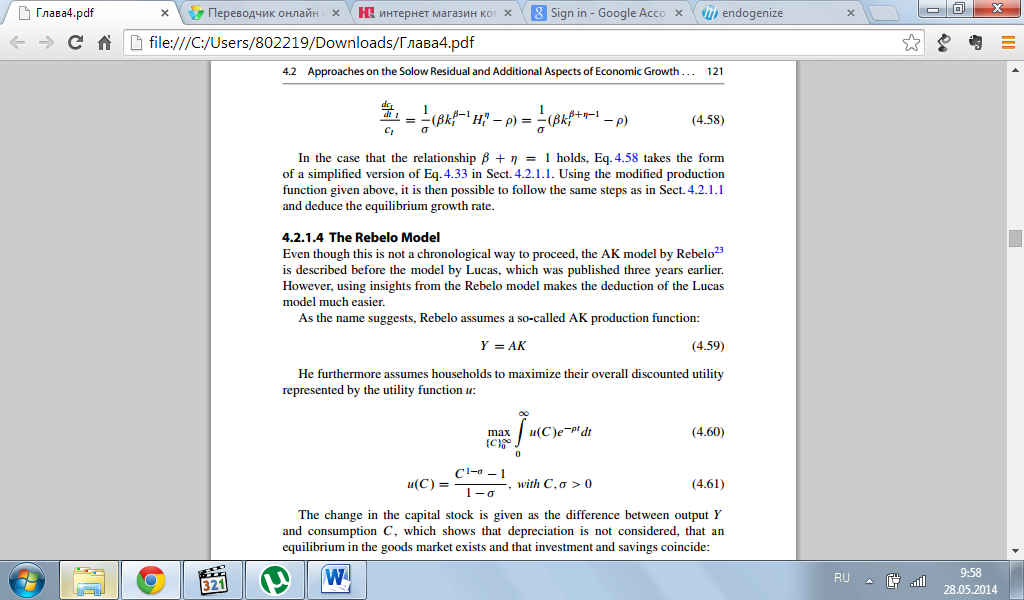
В случае, когда β+η= 1, ур.4.58 принимает форму упрощенного уравнения 4.33 в разделе 4.2.1.1. При помощи модернизированного производства функция, данная выше, может быть выполнена путем тех же шагов, как и в разделе 4.2.1.1 и далее находится равновесие темпов роста.

4.2.1.4. Модель Реберо

Даже при том, что это не хронологический способ изложения, модель AK Ребело описана перед моделью Лукасом, которая была опубликована тремя годами ранее. Однако использование знаний модели Ребело позволяет прозе понять модель Лукаса.

Само название предполагает, что Rebelo применяет так называемую производственную функцию AK:

Y=AK

Далее он предполагает, что домашние хозяйства максимизируют свою дисконтированную полезность, что выражается функцией полезности u:

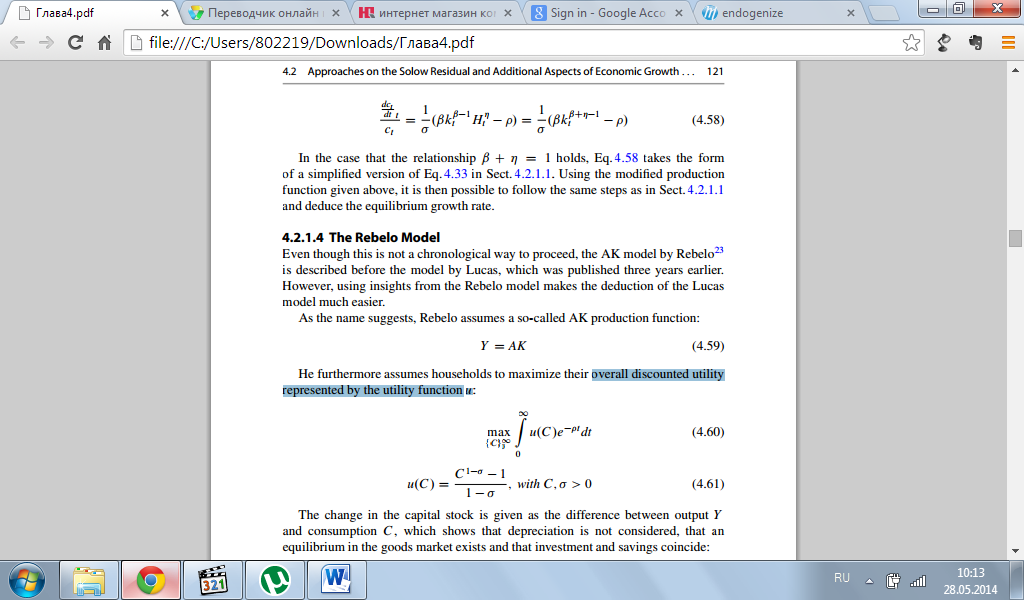
Изменение в акционерном капитале дано как разница между выпуском Y и потреблением C, которое показывает, что амортизацию не рассматривают и что равновесие на товарном рынке существует и что инвестиции и сбережения совпадают:

Используя тот же подход максимизации, что и в модели Рамсей-Касс-Купманса, закон Кейнса-Рамсея в этом случае записывается как:

Если уравнение 4.62 поделить на K, то равноверный уровень роста ϒ можно зписать как:

Перестановка этого уравнения позволяет записать темп роста устойчивого состояния следующим образом:

Поэтому, темп роста устойчивого состояния линейно пропорционален норме сбережений, а также уровню технологического прогресса.