4.2.1.1. Модель Рамсея-Касс-Купманса

Неоклассическая модель роста с эндогенной нормой сбережений обычно относится

к Модели Рэмси-Кэсс-Купмэнса. В некоторых случаях она называет сокращенно Модель Рэмси.

Модель предполагает, что существует большое количество домашних хозяйств, L, что остается постоянным в ходе модели; прирост населения является нулем в этом случае. Размещаем домашние хозяйства вдоль интервала [0;1], что гарантирует, что на долю домашних хозяйств приходятся совокупные акции тоже.

Кроме того, предполагается, что доход с труда выражается ставкой заработной платы w, а доход с капитала установлен нетто-ставкой дохода r- δ, посчитанный как разница между номинальной нормой доходности и нормой амортизации δ.

Средне статистический человек, как предполагается, максимизирует свою полезность в течение неограниченного периода времени. Фирмы, как предполагается, максимизируют свой прибыль.

Это означает, что домашние хозяйства должны решить следующую интертемпоральную проблему максимизации:

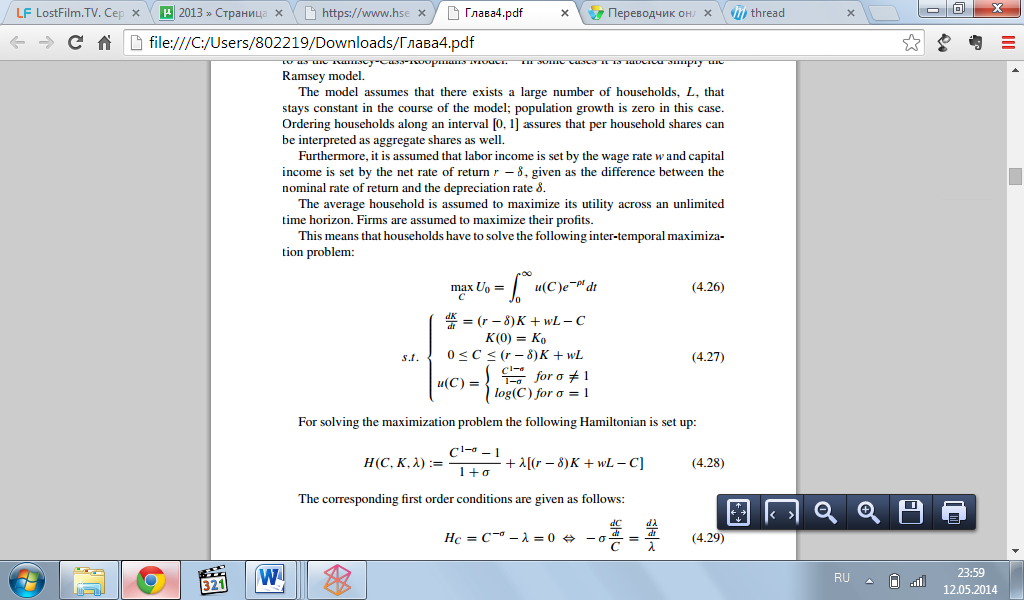
Для решения проблемы максимизации настроен следующий Гамильтониан:

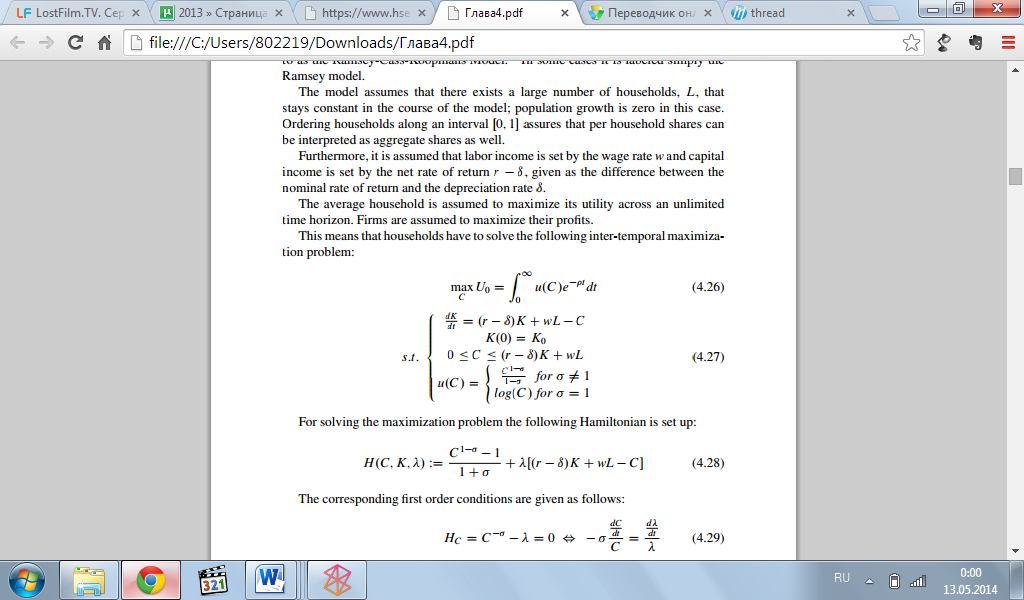
Соответственно, первые условия можно записать следующим образом:

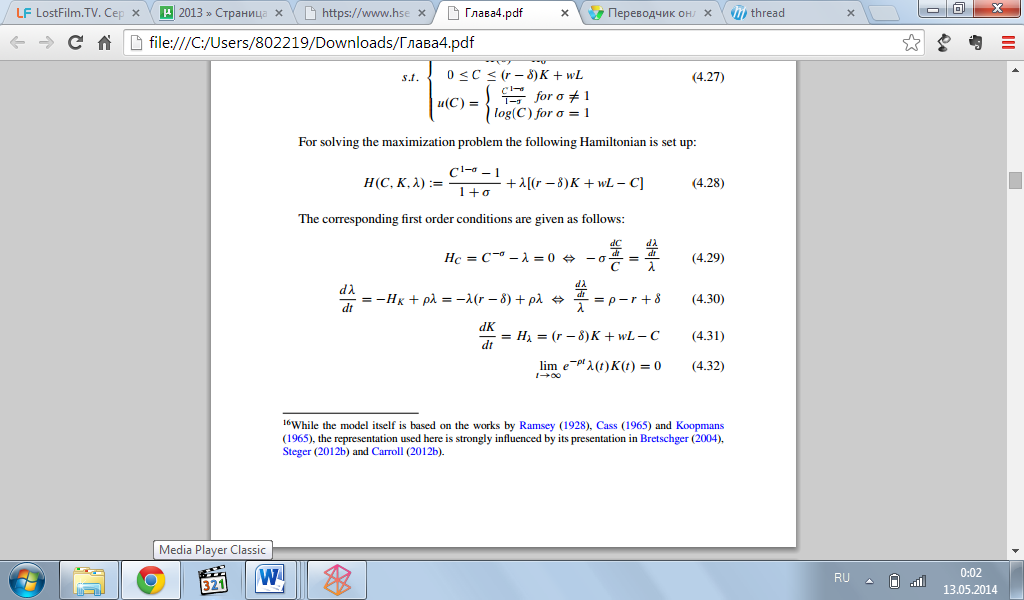
Переформулировав и скомбинировав уравнение 4.29 и 4.30, мы приходим к, так называемому, правилу Кейнса-Рамсея:

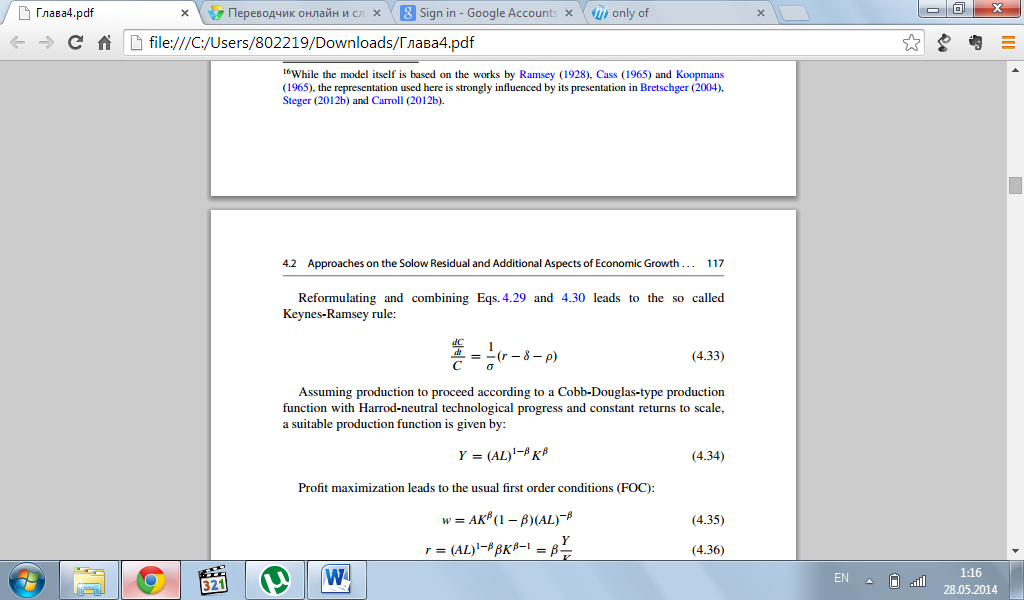
Предполагая, что производство идет согласно производственной функции типа Кобба- Дугласа с нейтральным технологическим прогрессом Харрода и постоянной отдачей на масштаба, дается подходящая производственная функция:

Максимизирование прибыли приводит к стандартному первому условию (ФОК):

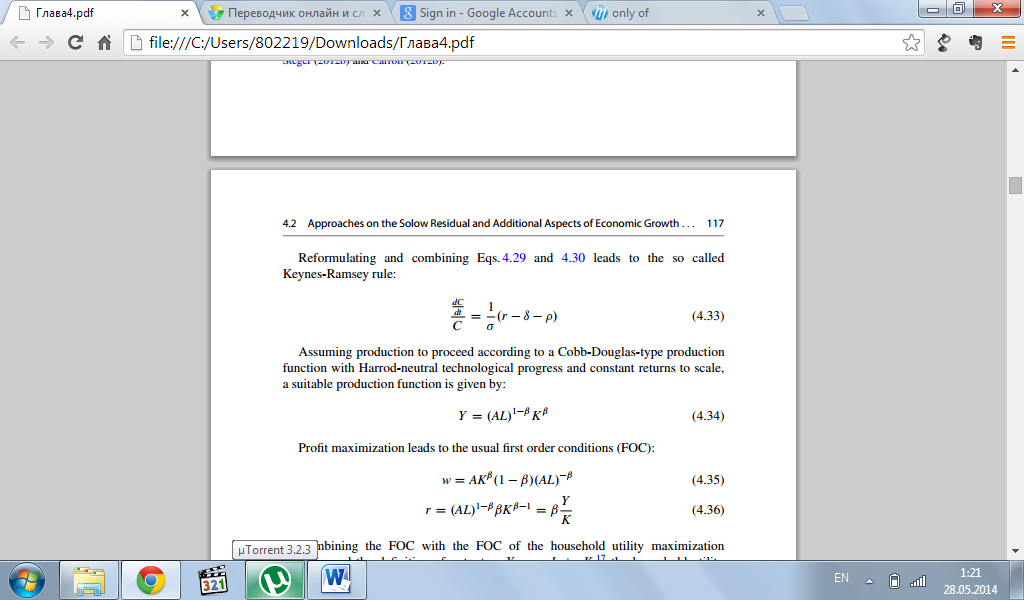
Комбинируя ФОК с ФОК домашних хозяйств, при условии Y=wL+ rK, тогда проблема предельной максимизации домашних хозяйств может быть сформулированна следующим образом:

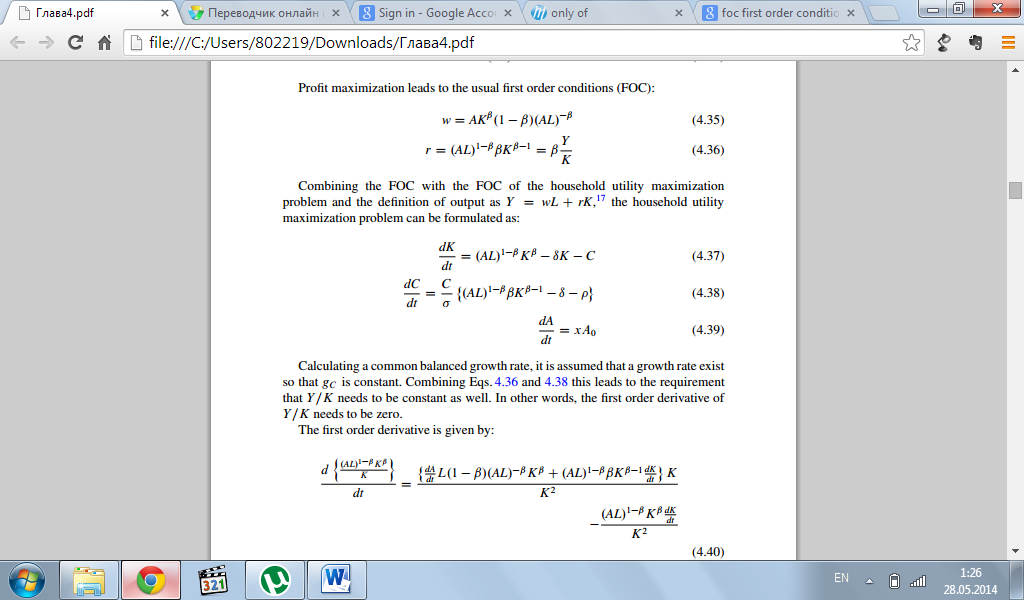
Считая сбалансированную ставку роста, предполагается, что существующая ставка такая, что Gc= const. Возьмем уравнения 4.36 и 4.38. при их изучении было выявлено, что нужно предположение, что Y/K также является константой. Другими словами, приравниваем к нулю. Тогда полученное уравнение можно записать, как:

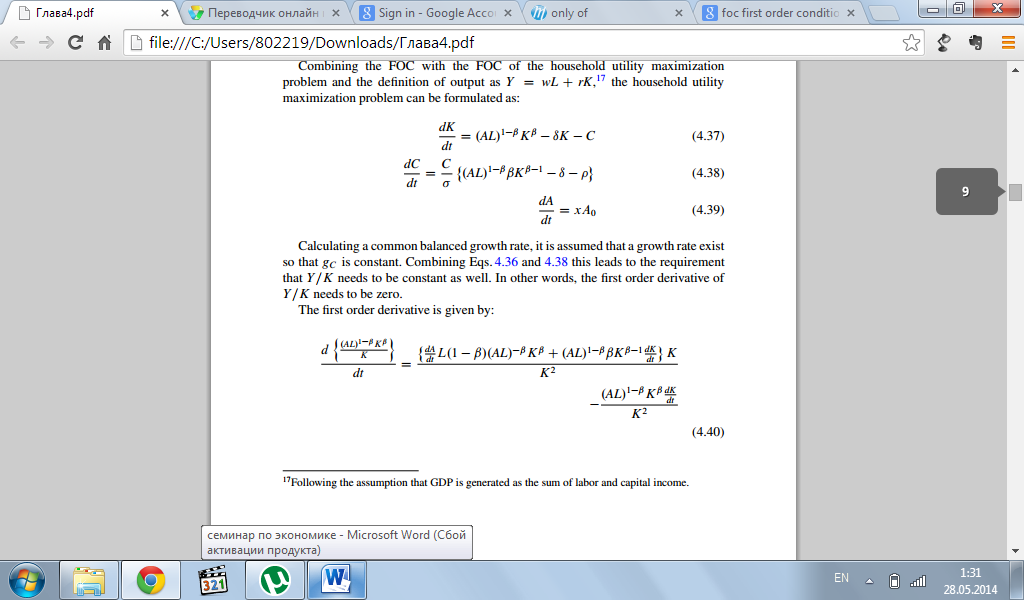
Приравниваем dY/K/dt к нулю:

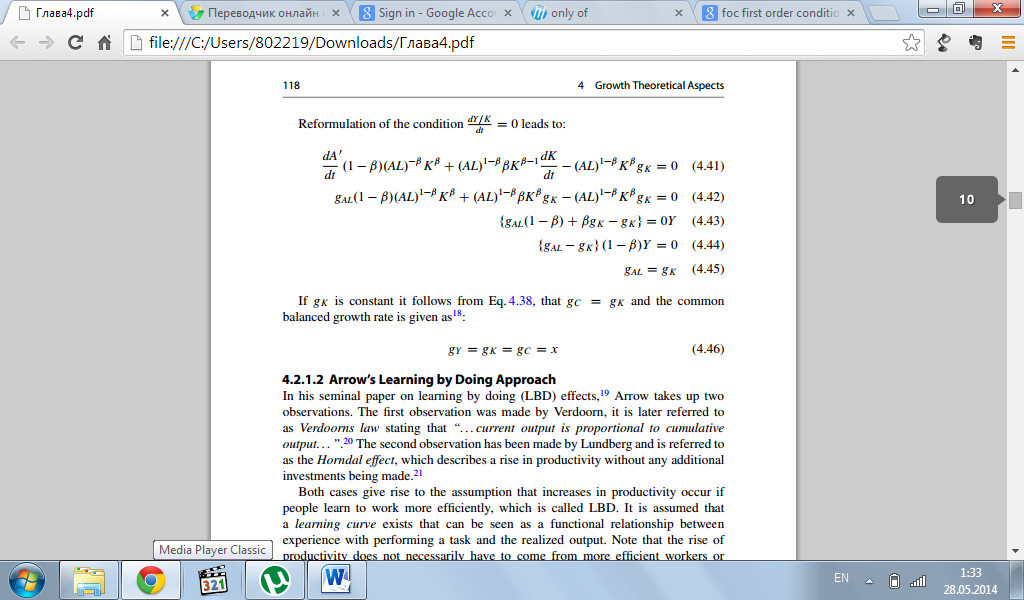
Если g с индексом K является константой, тогда исходя из уравнения 4.38 о том, что Gc=Gk, можно сделать вывод, что ставка роста записывается как:

4.2.1.2. Подход Эрроу: обучение посредством практики

В его оригинальной статье об обучении на практике (LBD) эффектах, Эрроу использует два допущения. Первое наблюдение было сделано Вердурном, которое позже именуется как закон Вердуна, заявляющий: “... текущая производительность пропорциональна кумулятивному результату..”. Второе наблюдение было сделано Лундбергом и именуется как эффект Horndal, который описывает повышение производительности без дополнительных инвестиций.

Оба случая дают начало предположению, что увеличение производительности происходит, если люди учатся работать более эффективно, которое называется LBD. Предполагается, что кривая обучения существует, которая считается как функциональное отношение между опытом выполнения задач и реализованным результатом. Обратите внимание на то, что повышение производительности должно происходить не только благодаря приходу большего количества эффективных работников или возрастающего уровня практических знаний, но может быть вследствие косвенно реализованных инновационных процессов, которые являются результатом процесса обучения. Поэтому, иногда используемое выражение отношение прогресса, а не кривая обучения, лучше подходит для описания эффектов LBD, оказывающих влияние на фирмы.

Идея LBD будет играть только вторичную роль в ходе этого исследования;

поэтому идеи Эрроу реализованы только в контексте производственной функции, которая посчитывается с помощью эффекта LBD.

С игнорированием амортизации Эрроу, обозначим Kt как уровень кумулятивных

валовых инвестиций в период t, ϒ(K) - объём выпуска, где кумулятивные инвестиции являются K, и χ(К) как сумма затрат на трудовые ресурсы, используемые в производственном процессе, при условии, что кумулятивные инвестиции находятся на уровне K.

Таким образом, общий выпуск продукции Y и рабочая сила L даны как (где Ʌ и Г являются заменой соответственно альфы и гаммы):

Отсутствие амортизации Kt делает функцию монотонно увеличивающейся, что

приводит к монотонным функциям χ и ϒ и сохраняет их строго положительными.

Поэтому, функции Ʌ и Г являются обратимыми, и второе уравнение может быть записано как:

Подставим в первое уравнение, тогда:

Уравнение 4.50 может быть прочитано как производственная функция с входными факторами труда L и акционерным капиталом K.

Кроме того, Эрроу находит особый случай, где он вводит идею кривых обучения. Он принимает функцию ϒ(Kt) за постоянную – ϒ(Kt) =а – и χ(Kt), эффект кривой обучения принимает за ϒ(Kt) =b(Kt)^-n. Он дает определение фактическим кривым обучения для производства «воздушной» структуры. Здесь n является склонностью ассимилировать новое знание. Если n больше, те же инвестиции требовали бы меньшего количества труда, чтобы произвести соответствующий результат. Функция ϒ является настолько постоянной, насколько это позволяло бы быть постоянными отношение выпуска капиталу и линейному соотношению между инвестициями и выпуском.

Используя эти функции производственная функция, упомянутая в ур.4.50, читается как:

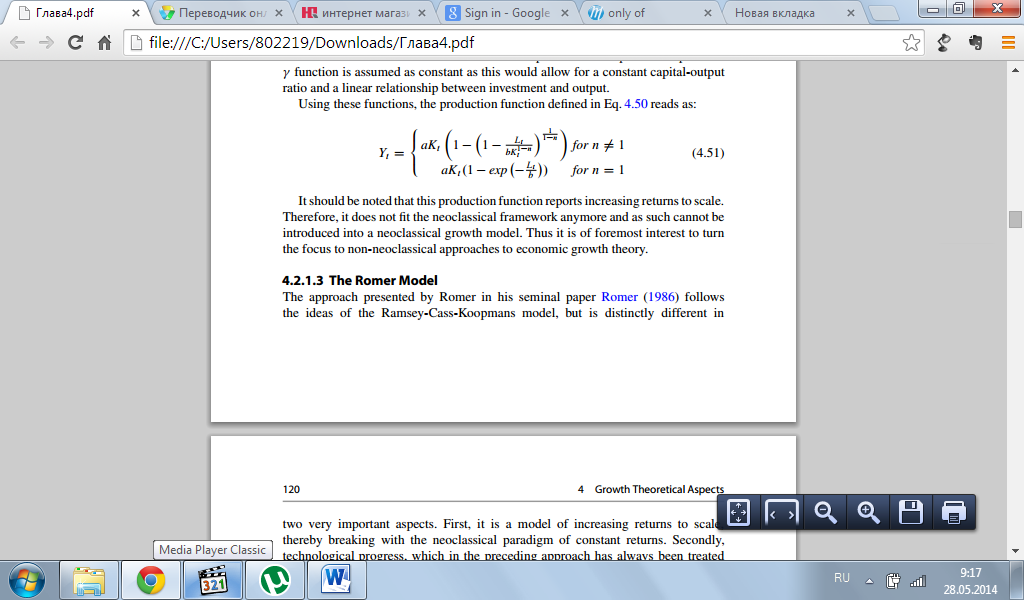
Нужно отметить, что эта производственная функция ведет к увеличению отдачи от масштаба. Поэтому, она больше не соответствует неоклассической структуре и не может быть введена в неоклассическую модель роста. Таким образом, лучше сфокусироваться не на неоклассических подходах, а на теории экономического роста.