Задача № 18 Определение грузоподъемности балки

Дано: l=3м, r(b)=13см, сечение ○, № схемы -2, F₀/ql=-2, M₀/ql²=1, F₀=-2ql

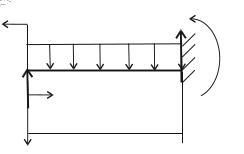
Рис.14 Заданная балка

Найдем опорные реакции:

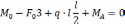
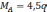
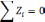
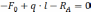
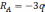
Определим М и Q:

Участок 0≤х≤3

Q(x)=F0-qx

x=0: Q(x)=6q

x=3: Q(x)=3q

M(x)= F0∙x+M0-q∙x∙x/2

x=0: M(x)=9q

x=3: M(x)=22,5q

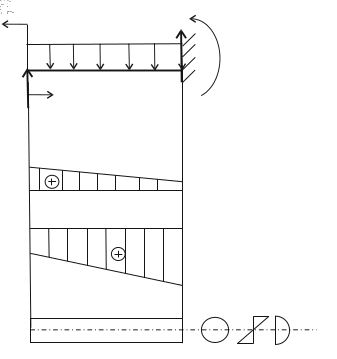
Рис.15 Эпюра М и Q

Опасные сечения:

а-а- где действует максимальный по модулю изгибающий момент,

b-b – где действует максимальная величина поперечной силы

Условие прочности: σmax≤[σ]=10МПа

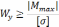
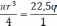
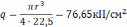
Проверим, выполняется ли условие прочности в точке с максимальными касательными напряжениями.

Условие прочности: τmax≤[τ]=2МПа

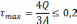
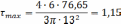
Условие прочности не выполняется. Произведем перерасчет q из условия прочности в точке 2. τmax≤[τ]=2Мпа

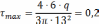
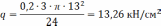
Ответ: q=13,26 кН/см²

Задача № 19 Определение грузоподъемности чугунной балки моносимметричного сечения, работающей в условиях плоского изгиба

Дано: схема № 5, b=15 см, t=0,8см, h=30 см, δ=1см, l=2м, № схемы (рис.18) -1, M1/ql²=1

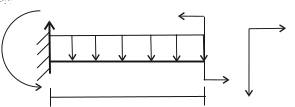
Рис. 16 Заданная балка

Найдем опорные реакции:

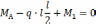
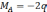
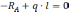
Определим М и Q:

Участок 0≤х≤2

Q(x)=-qx

x=0: Q(x)=0

x=2: Q(x)=-2q

M(x)= M1-q∙x∙x/2

x=0: M(x)=4q

x=2: M(x)=2q

Рис. 17 Эпюры М и Q

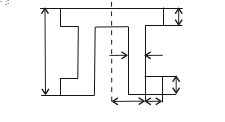
Рис. 18 Поперечное сечение балки

Найдем геометрические характеристики заданного поперечного сечения: осевые моменты инерции относительно главных центральных осей. Сечение имеет только одну ось симметрии, эта ось является одной из главных осей инерции, назовем ее z. Вторая главная ось – у, проходящая через центр тяжести сечения.

Положение центра тяжести: zцт=Sa/A

Разобьем сечение на 5 фигур: полку, 2 стенки, 2 ребра.

A=2Ac+An+2Ap

Ось а-а расположим так, чтобы статический момент одной из фигур равнялся 0.

Sa=2(h-2t)δ∙((h-2t)/2+t/2)+2(2t+δ)t(t/2+t/2+h-2t)=950,78

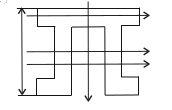
Рис.19 Расположение главных осей сечения

Определим осевой момент инерции относительно оси у:

Уу=У_у0 + Аа²

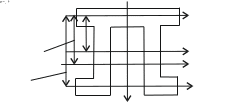
Рис. 20 Поперечное сечение балки

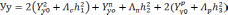
h1=15,197-14,6=0,597

h2=15,197

h3=29,2-15,197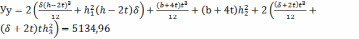

Чугун-хрупкий материал, и хрупкость при растяжении у него меньше прочности при сжатии.

Максимальный момент положителен, то есть балка в сечении, где действует Мmax изгибается выпуклостью вниз и растягивающие напряжения будут в нижних волокнах. Поэтому расположим поперечное сечение так, чтобы центр тяжести сечения был ближе к нижним волокнам, т.е. полкой вверх.

Найдем положение опасных сечений и опасных точек.

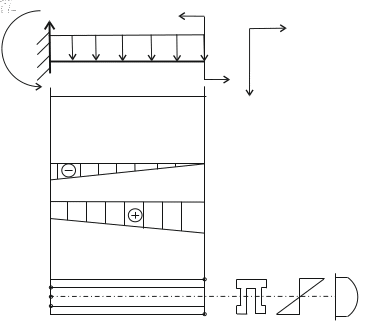
Рис.21 Эпюры М и Q, положение опасных сечений

Определим допускаемую нагрузку из условия прочности:

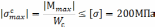
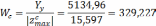
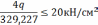
q=1646 кН

Проверим прочность в остальных опасных точках:

Точка 1’:

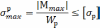
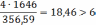
Условие прочности не выполнено.

Тогда:

4q/356,59≤6

q=534,88 кН

Точка 2 (по теории Мора)

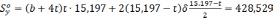
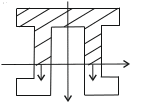
Рис. 22 Поперечное сечение

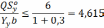
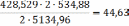
Условие прочности не выполнено.

Тогда,

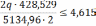
q=55,3

Точка 3

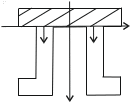
Рис. 23 Поперечное сечение

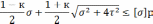
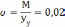
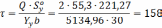
Условие выполнено.

Ответ: q=55,3 кН