Часть 2 Определение грузоподъемности расчетом по предельному пластическому состоянию

При увеличении F сверх допустимого значения σ растет прямо пропорционально нагрузке, при увеличении F до некоторой величины F>[F] напряжение σ2 во втором стержне достигнет σт, а усилие N2 – предельного значения, при этом σ1˂σт. Далее, при увеличении нагрузки, когда σ1 достигнет σт – система переходит в предельное состояние, F=Fпред, N1=N1пред, N2=N2пред.

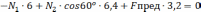
Fпр/F=193,725/107,06=1,8

При расчете на прочность данной системы по предельной нагрузке грузоподъемность увеличивается на 40%.

Часть 3. Определение дополнительных напряжений, вызванных неточностью изготовления стержня 1.

Рис.14 План перемещений при неточности изготовления стержня О₁В

Так как стержень О₁В изготовлен короче, чем требуется, в нем возникнет дополнительное напряжение, которое будет стремиться сжать стержень, конец О₁В при этом поднимется на некую величину δ1, а стержень О₂С растянется на δ₂.

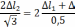
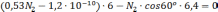
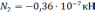
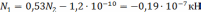
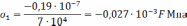
Ответ: σ₁=-0,027∙10^-3Мпа, σ₂=-0,09∙10^-3Мпа.

Задача №6 Определение грузоподъемности статически неопределимой шарнирно-стержневой конструкции (п.3)

Рис.15 Заданная шарнирно-стержневая конструкция

Дано: l₁=2,5 м, α=45^о, А₁=20 см², № схемы -2, l₂=2,5м, А₂=40см², β=60^о, γ=30^о, А₃=15 см², материал-дюралюминий.

Заданная система имеет 3 деформируемых стержня, 1 из которых лишний, так как система один раз статически неопределима.

В предельном состоянии должны потечь 2 стержня. Возможны 3 варианта предельного равновесия конструкции:

1. Текут стержни 2 и 3.

2. Текут стержни 2 и 1.

3. Текут стержни 1 и 3.

Вариант 1.

Допустим, что напряжения в стержнях 2 и 3 равны σ_т, а стержень 1 работает упруго.

Рассмотрим план перемещений, при этом будем считать, что стержень 1 – абсолютно жесткий.

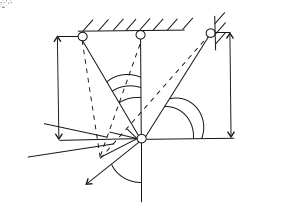
Рис.16 План перемещений при деформации стержней 2 и 3.

Рис.17 План сил при деформации стержней 2 и 3.

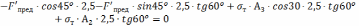
Вариант 2.

Допустим, что напряжения в стержнях 1 и 2 равны σ_т, а стержень 3 работает упруго.

Рассмотрим план перемещений, при этом будем считать, что стержень 3 – абсолютно жесткий.

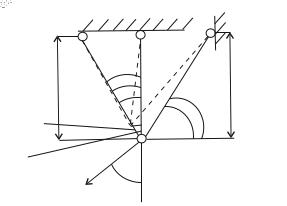
Рис. 18 План перемещений при деформации стержней 1 и 2.

Рис.19 План сил при деформации стержней 1 и 2

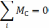
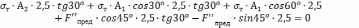
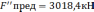
Вариант 3.

Допустим, что напряжения в стержнях 1 и 3 равны σ_т, а стержень 2 работает упруго.

Рассмотрим план перемещений, при этом будем считать, что стержень 2 – абсолютно жесткий.

Рис. 20 План перемещений при деформации стержней 1 и 3.

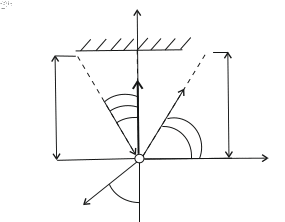
Рис. 21 План сил при деформации стержней 1 и 3.

Ответ: фактическая допускаемая нагрузка – минимальная из трех полученных, т.е. Fпред=525кН

Задача № 7 Исследование плоского напряженного состояния по заданным напряжениям на произвольных площадках. Проверка прочности.

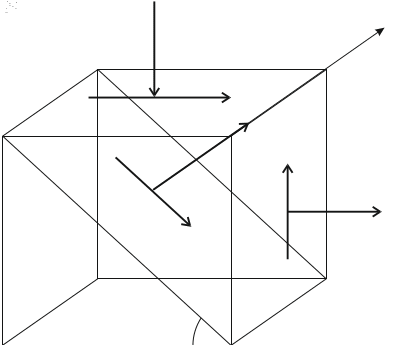
Рис.22 Схема напряженного состояния элемента

Дано: № схемы 2, σх=20МПа, σz=-40МПа, τxz=-10МПа, β=45^о,σпред=160/480, материал – чугун.

Изобразим элемент в виде плоского рисунка, на котором указана система координат.

Рис. 23 Плоская система напряженного состояния элемента

Аналитический способ

Определим нормальное и касательное напряжения, используя угол αn между нормалью n и осью z, отсчитывая его от z к n.

Абсолютная величина полного напряжения:

Определение главных напряжений и главных направлений.

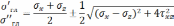
Пронумеруем главные напряжения по убыванию:

σ₁=21,62МПа,σ₂=0, σ₃=-41,62МПа

Найдем положение главных площадок. Вычислим углы α’гл, α’’гл, определяющие положение главных площадок (будем отсчитывать эти углы от направления оси х).

Рис.24 Определение положения главных площадок

Выясним, какому из напряжений соответствует угол α’гл:

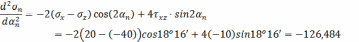
Знак отрицательный, следовательно, на этой площадке действует большее из найденных главных напряжений – σ₁.

Рис.25 Определение положения главных напряжений

Определение величин наибольших касательных напряжений.

Так как σ’гл=σ₁, σ’’гл=σ₃, поэтому max τ является максимальным среди касательных напряжений для всей совокупности площадок, проходящих через заданную точку: max τ =τ_max

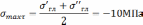
Рис. 26 Определение величин наибольших касательных напряжений

Графический способ исследования напряженного состояния

Построим круг напряжений Мора, изобразим систему координат σоτ с одинаковым масштабом по вертикальной и горизонтальной осям. Отметим 2 точки x,z, соответствующие заданным площадкам с нормалями x, z.

Точкам I, III пересечения круга с горизонтальной осью соответствуют главные площадки 1,3. Горизонтальные координаты этих точек являются главными напряжениями: σ1≈20МПа, σ3≈-42МПа.

Углы α1, α3 определяют положение главных площадок.

Графически 2α₁≈18^о, 2α₃≈180^о+18^о≈198^о

Площадке, по которой действует максимальное касательное напряжение, соответствует точка К круга. Координаты точки К дают значения: maxτ≈30МПа, σ_maxτ=-10МПа.

Найдем с помощью круга напряжений напряжения по наклонной площадке. Построим на круге точку N, соответствующую наклонной площадке. Для этого отложим от радиуса ох против часовой стрелки угол α_n=45^o. Координаты точки N дают напряжения на наклонной площадке: σт=0, τ_n≈30МПа.

Рис. 27 Круг напряжений

Проверка прочности

По условию задачи материал элемента – хрупкий. При проверке прочности используем теории прочности, относящиеся к хрупким материалам.