Уравнение плоскости в отрезках.

Уравнение плоскости вида  , где a, b и c – отличные от нуля действительные числа, называется уравнением плоскости в отрезках. Абсолютные величины чисел a, b и c равны длинам отрезков, которые отсекает плоскость на координатных осях Ox, Oy и Oz соответственно, считая от начала координат. Знак чисел a, b и c показывает, в каком направлении (положительном или отрицательном) следует откладывать отрезки на координатных осях.

Нормальное уравнение плоскости.

Общее уравнение плоскости вида   называют нормальным уравнением плоскости, если длина вектора   равна единице, то есть, 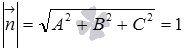 , и  .

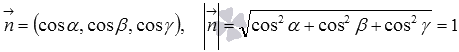Часто можно видеть, что нормальное уравнение плоскости записывают в виде  . Здесь   - направляющие косинусы нормального вектора данной плоскости единичной длины, то есть  , а p – неотрицательное число, равное расстоянию от начала координат до плоскости.