9. Гипербола, каноническое уравнение. Эксцентриситет и директриса гиперболы.

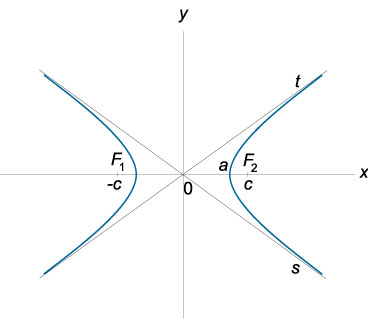
Г ипербола представляет собой плоскую кривую, для каждой точки которой модуль разности расстояний до двух заданных точек является постоянным. Расстояние между фокусами гиперболы называется фокусным расстоянием и обозначается через 2c. Середина отрезка, соединяющего фокусы, называется центром. У гиперболы имеются две оси симметрии: фокальная или действительная ось, проходящая через фокусы, и перпендикулярная ей мнимая ось, проходящая через центр. Действительная ось пересекает ветви гиперболы в точках, которые называются вершинами. Отрезок, соединяющий центр гиперболы с вершиной, называется действительной полуосью и обозначается через a. Мнимая полуось обозначается символом b. Каноническое уравнение гиперболы записывается в виде

1. Модуль разности расстояний от любой точки гиперболы до ее фокусов является постоянной величиной:  |r₁ − r₂| = 2a,  где r₁, r₂ − расстояния от произвольной точки P(x, y) гиперболы до фокусов F₁ и F₂,a − действительная полуось гиперболы.

У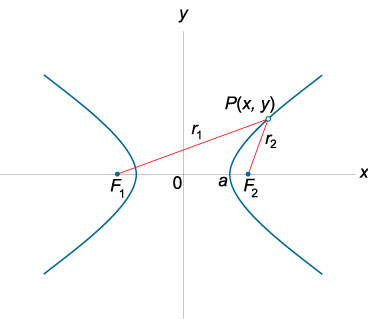 равнения асимптот гиперболы 

3. Соотношение между полуосями гиперболы и фокусным расстоянием  c² = a² + b²,  где c − половина фокусного расстояния, a − действительная полуось гиперболы, b − мнимая полуось.

Эксцентриситет гиперболы e = c/a > 1 

Уравнения директрис гиперболы  Директрисой гиперболы называется прямая, перпендикулярная ее действительной оси и пересекающая ее на расстоянии a/e от центра. У гиперболы − две директрисы, отстоящие по разные стороны от центра. Уравнения директрис имеют вид 

Общее уравнение гиперболы:Ax² + Bxy + Cy² + Dx + Ey + F = 0,  где B² − 4AC > 0.

Общее уравнение гиперболы, полуоси которой параллельны осям координат  Ax² + Cy² + Dx + Ey + F = 0,  где AC < 0.

10. Парабола, каноническое уравнение. Эксцентриситет и директриса параболы

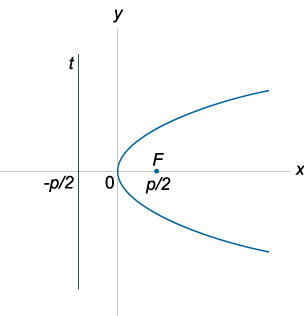
Параболой называется плоская кривая, в каждой точки которой выполняется следующее свойство: расстояние до заданной точки (фокуса параболы) равно расстоянию до заданной прямой (директрисы параболы). Расстояние от фокуса до директрисы называется параметром параболы и обозначается через p. Парабола имеет единственную ось симметрии, которая пересекает параболу в ее вершине. Каноническое уравнение параболы имеет вид: y = 2px.

Уравнение директрисы: x = −p/2,  где p − параметр параболы.

     

Эксцентриситет: Координаты фокуса: F(p/2, 0) Координаты вершины M(0, 0)

Общее уравнение параболы Ax² + Bxy + Cy² + Dx + Ey + F = 0, где B² − 4AC = 0.

Уравнение параболы, ось симметрии которой параллельна оси Oy: Ax² + Dx + Ey + F = 0   (A ≠ 0, E ≠ 0),  или в эквивалентной форме: y = ax² + bx + c,   p = 1/(2a)

Уравнение директрисы: y = y₀ − p/2, где p − параметр параболы.

Координаты фокуса: F(x₀, y₀ + p/2)

Координаты вершины:

У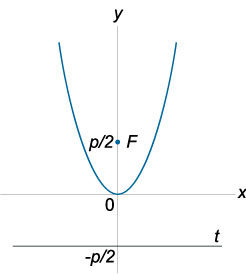 равнение параболы с вершиной в начале координат и осью симметрии, параллельной оси Oy  y = ax²,   p = 1/(2a)

Уравнение директрисы y = −p/2, где p − параметр параболы.

Координаты фокуса: F(0, p/2) Координаты вершины: M(0, 0)