1. Линейно зависимая и линейно независимая система векторов. Их свойства. База пространства и ранг системы векторов.

Определение. Векторы 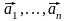называются линейно зависимыми, если существует такая линейная комбинация , при не равных нулю одновременно _i , т.е. .

Если же только при _i = 0 выполняется , то векторы называются линейно независимыми.

Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.

Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.

Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.

Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.

Свойство 6. Любые 4 вектора линейно зависимы.

ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ — частный случай по отношению к общему понятию линейной зависимости. Рассмотрим в качестве примера два произвольных ненулевых вектора, a и b, принадлежащих векторному пространству V.

Если можно подобрать такие не равные нулю числа α и β, что αa + βb = 0, то векторы a и b называются линейно зависимыми. Причина этого ясна: с помощью полученного равенства можно выразить, напр., вектор a через вектор b. Это значит, что a зависит от b. Можно обобщить это определение и на произвольное число векторов: если существуют такие отличные от нуля числа α1, ..., αn, что ∑αiai = 0, то векторы называются линейно зависимыми, если же такая система чисел отсутствует, то линейно независимыми.

БАЗИС ВЕКТОРНОГО ПРОСТРАНСТВА — набор из максимального (для данного пространства) числа линейно независимых векторов (см. Линейная зависимость векторов). Следовательно, все остальные векторы пространства оказываются линейными комбинациями базисных. Если все базисные векторы взаимно ортогональны, а длина каждого из них равна единице, то базис называется ортонормированным. Единичный базисный вектор называют ортом (обозначается ei, где i — номер координаты).

Каждый вектор пространства может быть представлен в виде линейной комбинации базисных векторов: a = ∑aiei. Коэффициенты разложения ai однозначно определяют вектор a. Поэтому часто говорят, что n-мерный вектор — это упорядоченная совокупность n чисел {ai}. (См. Вектор.) Размерность векторного пространства равна количеству векторов, составляющих его базис.

2. Система линейных алгебраических уравнении. Совместимость системы, Метод Гаусса. Правило Крамера.

С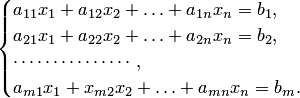 истемой   линейных алгебраических уравнений с   неизвестными называется система уравнений вида

Числа   называются коэффициентами системы;   — свободными членами,   — неизвестными. Количество   уравнений в системе может быть меньше, больше или равно числу   неизвестных. Решением системы называется упорядоченная совокупность   чисел   такая, что после замены неизвестных   соответственно числами   каждое уравнение системы превращается в верное числовое равенство. Система называется совместной, если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной.

Систему принято записывать в матричной форме. Для этого из коэффициентов системы составляем матрицу системы

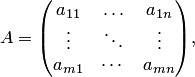
свободные члены записываем в столбец свободных членов

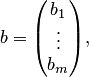
а неизвестные — в столбец неизвестных

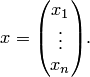
Матричная запись неоднородной системы уравнений (5.1) имеет вид а однородной: где символ   в правой части обозначает нулевой столбец размеров  .

Правило Крамера. Если определитель   матрицы системы   линейных уравнений с   неизвестными отличен от нуля, то система имеет единственное решение, которое находится по формулам

где   — определитель матрицы, полученной из матрицы системы заменой i-го столбца столбцом свободных членов, т.е.

В самом деле, рассмотрим систему (5.6) как матричное уравнение  . Так как определитель   матрицы   отличен от нуля, по теореме 4.2 заключаем, что матричное уравнение   имеет единственное решение: где   — обратная матрица. Запишем i-й элемент столбца  , учитывая, что в i-й строке присоединенной матрицы   стоят алгебраические дополнения i-го столбца матрицы 

Заметим, что в скобках записано разложение определителя   по i-му столбцу, т.е.  , что и требовалось доказать.

Метод Гаусса

1.Составить расширенную матрицу системы:

2. Используя элементарные преобразования над строками матрицы  , привести ее к ступенчатому виду. Если базисный минор матрицы   расположен в первых   строках и   столбцах, получится следующий вид:

3. Выяснить, совместна система или нет. Для этого определить ранги матриц   и 

 — число ненулевых строк в матрице  ;

Если   (при  ), то система не имеет решений. Процесс решения завершен. Если   (при  ), то система совместна. Процесс решения продолжается.

4. Для совместной системы   привести матрицу   к упрощенному виду. Для этого при помощи элементарных преобразований над строками добиваемся того, чтобы в каждом столбце, входящем в базисный минор, все элементы были равны нулю, за исключением одного, равного единице. Если базисный минор матрицы   расположен в первых   строках и первых   столбцах, то матрица приводится к упрощенному виду:

Первые Четыре пункта составляют прямой ход метода Гаусса. Далее применяется обратный метод Гаусса