Лабораторна робота №2

2.1. Основні теоретичні положення

Відмінність електричних кіл змінного струму від аналогічних кіл постійного струму полягає в тому, що математичний апарат для їх досліджень стає більш громіздким, адже у рівняннях використовуються напруги, які змінюються за гармонічними законами.

Для спрощення задач аналізу в електротехніці використовуються графічні методи. На рис. 2.1 продемонстровані два способи зображення синусоїдального сигналу.

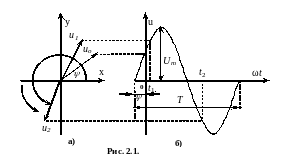
Рис. 2.1,б представляє синусоїдальний сигнал

як функцію часу з початковою фазою , амплітудою U_m та кутовою частотою

 = 2π / T, де T – період.

Рис. 2.1,а зображає гармонічний сигнал у вигляді радіус-вектору U_m, який обертається відносно початку координат з частотою 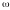проти годинникової стрілки. В момент часу t = 0 його положення визначається початковим фазовим кутом , а в моменти часу t₁, t₂ – відповідно, кутами (t₁ + ) та (t₂ + ).

У практиці використання змінних струмів широко використовується поняття діючої напруги, яка визначається як

.

Такі ж співвідношення справедливі і для струмів.

Такі ж співвідношення справедливі і для струмів.

Відповідно до визначення тригонометричної функції синуса, проекція радіус-вектору на вісь у визначається як:

,

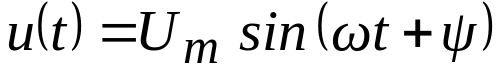а проекція на вісь х визначається функцією косинусу:

.

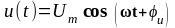Тобто, будь-якому радіус-вектору, який рівномірно обертається, однозначно відповідає синусоїдна функція і навпаки.

Представлення синусоїди у вигляді радіус-вектору дає можливість використовувати графічні способи представлення сигналів.

При використанні комплексної форми зображень координатні осі х та у замінюються відповідно на осі комплексної площини Re (Real) та Im(Imaging). При цьому, як відомо, будь-якому вектору A, що розміщується на комплексній площині, однозначно відповідає комплексне число, яке може бути записане в алгебраїчній, тригонометричній та показниковій (експоненціальній) типу е^x формах.

Алгебраїчна форма: .

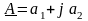Тригонометрична: 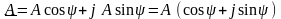. (2.1)

Експоненціальна: .

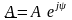Перехід від однієї форми до іншої забезпечується наступними формулами:

;	;
;	;
;	.

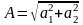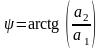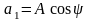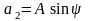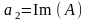Якщо 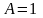, то справедливі співвідношення:

;	;
;	.

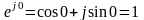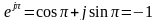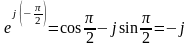А ктивнийопіру колі змінного струму.В електричному колі з активним опором при дії напруги

,

у відповідності з, струм матиме величину:

.

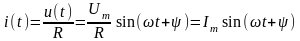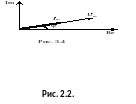
Струм за фазою співпадає з напругою і графічно може представлятись як у вигляді часових функцій, так і у вигляді векторних діаграм. Векторна форма має вигляд, що приведена на рис. 2.2.

Вектор напруги 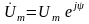має початковий кут 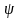. Вектор струму співпадає за фазою з вектором напруги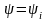, а та .

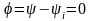С

б

а

а

ередня потужність є активною потужністю і може визначатись через діючі напруйу і струм:

.

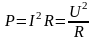О

б

диницею виміру активної потужності є ват [Вт], а енергії за інтервал часу Т – ват-секунда [Вт·с], W = PT.

Індуктивність у колі змінного струму.

г

Якщо в електричному колі з ідеальним індуктивним елементом Lдіє струм

,

то напруга на індуктивності випереджає струм за фазою на кут 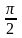, що пояснюється векторною діаграмою, зображеною на рис. 2.3.

Зв’язок між амплітудними значеннями напруги і струму:

.

Величина Х_L =L називається індуктивним опором.

Конденсатор у колі змінного струму. Коли до джерела змінної напруги

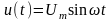
приєднаний конденсатор, то струм у колі випереджає напругу на (Рис. 2.4).

В

в

еличина називається ємнісним опором, а закон Ома для кола записується у вигляді:

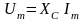або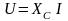 .