Монополия. Максимизация прибыли фирмой-ценоискателем. Социальные издержки монополии, ее неэффективность. Естественная монополия. Проблема минимального эффективного масштаба производства.
В предшествующих главах мы провели анализ поведения конкурентной отрасли — рыночной структуры, возникающей с наибольшей вероятностью тогда, когда в отрасли имеется большое число мелких фирм. В настоящей главе обратимся к противоположной крайности и рассмотрим такую отраслевую структуру, при которой в отрасли существует только одна фирма — монополия.
Когда на рынке действует только одна фирма, очень маловероятно, что она будет считать рыночную цену заданной. Вместо этого монополия признает свое влияние на рыночную цену и будет выбирать такой уровень цены и объем выпуска, которые максимизировали бы ее совокупную прибыль.
Конечно, она не может выбирать цену и выпуск независимо одно от другого: при каждой заданной цене монополия сможет продать лишь столько выпуска, сколько сможет поглотить рынок. Если она выберет высокую цену, то сможет продать лишь небольшое количество товара. Выбор цены и объема выпуска монополистом ограничен поведением потребителей в отношении спроса.
Можно представлять себе монополиста выбирающим цену и предоставляющим потребителям возможность выбора количества товара, которое они хотят купить по данной цене, а можно думать, что монополист выбирает предлагаемое им количество товара, позволяя потребителям решить, какую цену они готовы за него заплатить. Первый подход, возможно, выглядит более естественным, однако второй оказывается более удобным для анализа. Разумеется, при корректном использовании оба подхода эквивалентны.
23.1. Максимизация прибыли
Начнем с изучения стоящей перед монополистом задачи максимизации прибыли. Обозначим обратную кривую рыночного спроса через p(y), а функцию издержек через c(y). Пусть r(y) =p(y)y — функция общего спроса монополиста. Тогда задача максимизации прибыли для монополиста принимает вид
max r(y) — c(y).
y
Условие оптимума для этой задачи очевидно: в точке оптимального выбора объема выпуска предельный доход должен равняться предельным издержкам. Если бы предельный доход был меньше предельных издержек, фирме выгодно было бы уменьшить выпуск, поскольку экономия на издержках более чем компенсировала бы потерю дохода. Если бы предельный доход был больше предельных издержек, фирме выгодно было бы увеличить выпуск. Единственная точка, в которой у фирмы нет стимула менять объем выпуска, — это точка, в которой предельный доход равен предельным издержкам.
Алгебраически условие оптимизации можно записать как
MR = MC
или
.
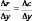То же самое условие MR = MC должно соблюдаться и в случае конкурентной фирмы; в этом случае предельный доход равен цене, и данное условие превращается в условие равенства цены предельным издержкам.
В случае монополиста член данного равенства, выражающий предельный доход, выглядит несколько сложнее. Если монополист решает увеличить выпуск на Dy, это оказывает на прибыль двоякое воздействие. Во-первых, он продает больший выпуск и получает от этого доход в размере pDy. Во-вторых, однако, монополист сбивает цену на величину Dp и выручает эту меньшую цену за весь продававшийся им объем выпуска.
Следовательно, общее воздействие, оказываемое на доход изменением выпуска на Dy, составит
Dr = pDy + yDp,
так что изменение общего дохода, деленное на изменение выпуска, — предельный доход — есть
.
(Эта формула выведена в точности так же, как и при обсуждении предельного дохода в гл. 15. Возможно, перед тем как продолжить изучение данной главы, стоит повторить этот материал.)
К рассматриваемой задаче можно подойти и по-другому — представить себе, что монополист выбирает цену и объем выпуска одновременно, признавая, конечно, при этом ограничение, накладываемое кривой спроса. Если монополист хочет продать больший объем выпуска, он должен снизить цену. Но цена эта будет более низкой для всех продаваемых им единиц выпуска, а не только для дополнительных. Поэтому появляется член yDp.
В случае конкурентной отрасли фирма, которая смогла бы снизить цену на свой товар по сравнению с ценой, запрашиваемой другими фирмами, немедленно захватила бы весь рынок, вытеснив с него своих конкурентов. В случае же монополизированной отрасли монополия и так имеет в своем распоряжении весь рынок; понижая цену на свой товар, она должна принимать во внимание влияние этого снижения на все продаваемые ею единицы выпуска.
Основываясь на обсуждении, проведенном в гл. 15, мы можем также выразить предельный доход через эластичность по формуле
MR(y)
= p(y)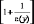 
и записать условие оптимальности "предельный доход равен предельным издержкам" как
p(y) 
= MC(y).
(23.1)
Поскольку коэффициент эластичности, естественно, отрицателен, можно бы также записать это выражение как
p(y) 
= MC(y).
С помощью этих уравнений легко увидеть связь данного случая со случаем конкурентной отрасли: при чистой конкуренции кривая спроса для фирмы является горизонтальной — бесконечно эластичной кривой спроса. Это означает, что 1/|e| = 1/Ґ = 0, так что данное уравнение, соответствующее случаю конкурентной фирмы, есть просто равенство цены предельным издержкам.
Обратите внимание на то, что монополист никогда не станет производить в неэластичной области кривой спроса. Ведь если |e| < 1, то 1/|e| > 1, и предельный доход отрицателен, так что он просто не может равняться предельным издержкам. Смысл этого становится ясен, если подумать о том, что подразумевается под неэластичной кривой спроса: если |e| < 1, то сокращение выпуска увеличит общий доход и одновременно должно сократить общие издержки, так что прибыль обязательно увеличится. Таким образом, любая точка, в которой |e| < 1, не может являться для монополиста точкой максимизации прибыли, поскольку он мог бы увеличить свою прибыль, производя меньший объем выпуска. Отсюда следует, что точка максимума прибыли может лежать только в области, где |e| ≥ 1.
.