17.3. Примеры технологии

Поскольку нам уже многое известно о кривых безразличия, легко понять, как пользоваться изоквантами. Рассмотрим несколько примеров технологий и соответствующих им изоквант.

Постоянные пропорции

Предположим, что наше производство — рытье ям и что яму можно вырыть единственным способом — используя одного человека и одну лопату. Ни дополнительные лопаты, ни дополнительные люди ничего не стоят. Таким образом, общее число ям, которое может быть вырыто, будет определяться минимумом имеющегося у вас числа людей и лопат. Мы записываем соответствующую производственную функцию в виде f(x₁, x₂) = min {x₁, x₂}. Изокванты имеют вид, представленный на рис.17.2. Обратите внимание на то, что эти изокванты выглядят точно так же, как кривые безразличия для случая совершенных комплементов в теории поведения потребителей.

 

 

 

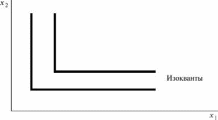
Рис. 17.2

Постоянные пропорции. Изокванты для случая постоянных пропорций.

 

Совершенные субституты

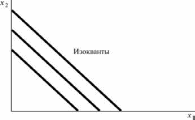
Предположим теперь, что мы производим домашние задания и факторами производства являются красные и синие карандаши. Количество произведенных домашних заданий зависит только от общего числа карандашей, поэтому мы записываем производственную функцию как f(x₁, x₂) = x₁ + x₂. Соответствующие изокванты, как показано на рис.17.3, выглядят в точности так же, как кривые безразличия для случая совершенных субститутов в теории поведения потребителей.

Производственная функция Кобба—Дугласа

Если производственная функция имеет вид f(x₁, x₂) = A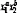 , то мы говорим, что это производственная функция Кобба—Дугласа. Она имеет в точности такой же вид, как и изученная нами ранее функция, описывающая предпочтения Кобба—Дугласа. Для функции полезности численное значение роли не играло, поэтому мы считали A = 1 и обычно выбирали a + b = 1. Однако численное значение производственной функции существенно важно, поэтому теперь следует допустить принятие этими параметрами произвольных значений. Параметр A измеряет, грубо говоря, масштаб производства: объем выпуска, который мы получили бы, если бы использовали по одной единице каждого фактора производства. Параметры a и b показывают, как реагирует объем выпуска на изменения количеств применяемых факторов производства. Значение этих параметров мы исследуем более детально далее. В некоторых примерах для того чтобы упростить расчеты, будем выбирать A = 1.

 

 

 

Совершенные субституты. Изокванты для случая совершенных субститутов.

Рис. 17.3

 

 

Изокванты Кобба—Дугласа имеют ту же самую симпатичную стандартную форму, что и кривые безразличия Кобба—Дугласа; как и в случае функций полезности, производственная функция Кобба—Дугласа — это, пожалуй, простейший пример стандартных изоквант.

17.5. Предельный продукт

Допустим, что мы производим в некоторой точке (x₁, x₂) и размышляем о том, не употребить ли чуть больше фактора 1, оставив количество фактора 2 без изменений на уровне x₂. Сколько дополнительного выпуска мы получим в расчете на дополнительную единицу фактора 1? Мы должны посмотреть, какое изменение выпуска приходится на единичное изменение фактора 1:

 

  .

 

Это отношение мы называем предельным продуктом фактора 1. Предельный продукт фактора 2 определяется аналогичным образом, и мы обозначим указанные предельные продукты соответственно MP₁(x₁, x₂)и MP₂(x₁, x₂).

При использовании понятия "предельный продукт" мы будем иногда допускать некоторую небрежность, описывая его как добавочный выпуск, получаемый от применения еще "одной" единицы фактора 1. Это утверждение вполне удовлетворительно до тех пор, пока "одна" единица мала относительно общего используемого нами количества фактора 1. Но следует помнить, что предельный продукт есть отношение изменений: добавочный объем выпуска, приходящийся на единицу добавочного количества фактора.

Понятие предельного продукта сходно с описанным нами в ходе обсуждения теории поведения потребителей понятием предельной производительности; различие между ними определяется лишь порядковой природой полезности. В настоящей главе речь идет о физическом выпуске: предельный продукт фактора есть конкретная численная величина, которая, в принципе, может наблюдаться в действительности.