14.8 Компенсирующая и эквивалентная вариации дохода

 

Теория излишка потребителя выглядит очень привлекательной в случае квазилинейной функции полезности. Даже если функция полезности не квазилинейна, излишек потребителя может по-прежнему служить разумной мерой благосостояния потребителя в целом ряде применений. Ошибки в измерении кривых спроса обычно перевешивают ошибки, связанные с приближенными подсчетами, сопутствующими использованию излишка потребителя в качестве меры благосостояния.

Может оказаться, однако, что для некоторых применений такой приближенный подсчет недостаточен. В настоящем параграфе мы в общих чертах охарактеризуем способ измерения "изменений полезности", при котором излишек потребителя не используется. На самом деле, речь пойдет о двух самостоятельных вопросах. Первый вопрос касается того, как вывести оценочную функцию полезности, если из наблюдений известен ряд вариантов потребительского выбора. Второй вопрос касается того, как можно измерить полезность в денежных единицах.

Проблема оценки вида функции полезности нами уже рассматривалась. В гл.5 мы привели пример того, как вывести оценочную функцию полезности Кобба-Дугласа. Как мы  заметили в этом примере, в случае функции спроса Кобба-Дугласа доли расходов на каждый товар сравнительно постоянны и поэтому в качестве оценочного значения параметров функции полезности Кобба-Дугласа можно использовать среднюю долю расходов. Если бы поведению потребителя в отношении спроса не была присуща эта конкретная черта, нам бы пришлось выбрать более сложную функцию полезности, но принцип оставался бы тем же самым: если у нас имеется достаточно наблюдений за поведением в отношении спроса и это поведение согласуется с максимизацией чего-либо, то, как правило, мы можем вывести оценочную функцию, которая максимизируется.

Как только мы получаем оценочную функцию полезности, описывающую какое-то наблюдаемое поведение в отношении потребительского выбора, мы можем использовать ее для оценки влияния предлагаемых изменений в области цен и объемов потребления. Это — лучшее, на что мы можем рассчитывать на самом фундаментальном уровне анализа. Значение имеют лишь предпочтения потребителя; одна функция полезности, описывающая данные предпочтения потребителя, не хуже другой.

Однако, в некоторых применениях удобным оказывается использование определенных денежных меры полезности. Например, мы могли бы поставить вопрос следующим образом: сколько денег надо дать потребителю, чтобы компенсировать ему изменение структуры его потребления. Мерой этого типа измеряется, по существу, изменение полезности, но делается это в денежных единицах. Какими удобными способами можно это сделать?

Предположим, что мы рассматриваем ситуацию, изображенную на рис.14.4. Здесь потребителю первоначально заданы какие-то цены ( ), и он потребляет некий набор ( ). Затем цена товара 1 возрастает с   до  , и потребитель переходит к потреблению набора ( ). Насколько большой ущерб благосостоянию потребителя наносит это изменение цены?             

 

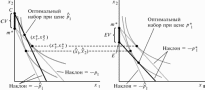
                                                A                                              B

Рис.14.4 Компенсирующая и эквивалентная вариации дохода. На рис.A показана компенсирующая вариация дохода (CV), а на рис.B — эквивалентная вариация дохода (EV).

 

Один из способов ответа на данный вопрос состоит в том, чтобы спросить, сколько денег следует дать потребителю после изменения цены, чтобы его благосостояние осталось точно таким же, каким оно было доизменения цены. Применительно к графической иллюстрации, мы спрашиваем, как сильно вверх мы должны сдвинуть новую бюджетную линию, чтобы она стала касательной к кривой безразличия, проходящей через точку исходного потребления ( ). Изменение дохода, необходимое для того, чтобы потребитель вновь оказался на исходной кривой безразличия, называется компенсирующей вариацией дохода, так как оно представляет собой такое изменение дохода, которое как раз компенсирует потребителю влияние изменения цены. Компенсирующая вариация дохода показыет, сколько денег правительство должно было бы добавить потребителю, если бы хотело в точности компенсировать ему изменение цены.

Другой способ измерить влияние изменения цены в денежных единицах состоит в том, чтобы спросить, сколько денег следовало бы забрать у потребителя до изменения цены, чтобы его благосостояние было точно таким же, каким оно стало после изменения цены. Эта мера называется эквивалентной вариацией дохода, поскольку она представляет собой изменение дохода, которое, с точки зрения полезности, эквивалентно изменению цены. Применительно к рис.14.4 мы спрашиваем, как сильно вниз мы должны сдвинуть исходную бюджетную линию, чтобы как раз коснуться кривой безразличия, проходящей через новый потребительский набор. Эквивалентная вариация дохода показывает максимальную величину дохода, с которой потребитель готов был бы расстаться, чтобы избежать изменения цены.

Вообще, та сумма денег, которую потребитель был бы готов заплатить, чтобы избежать изменения цены, как правило, отличается от той суммы денег, которую следовало бы выплатить потребителю, чтобы компенсировать ему изменение цены. В конце концов, при разных комбинациях цен стоимость доллара для потребителя различна, поскольку на него он может приобрести разные величины потребления.

Выражаясь языком геометрии, компенсирующая и эквивалентная вариации дохода — не что иное как два различных способа измерить то, "как далеко отстоят друг от друга" две кривых безразличия. В каждом из случаев мы измеряем расстояние между двумя кривыми безразличия расстоянием между касательными к ним. Вообще, эта мера расстояния будет зависеть от наклона касательных — то есть, от выбранных нами цен, определяющих наклон бюджетных линий.

Однако, компенсирующая и эквивалентная вариации дохода одинаковы в одном важном случае — при квазилинейной функции полезности. В этом случае кривые безразличия параллельны, так что расстояние между кривыми безразличия, как показано на рис.14.4, остается одним и тем же, независимо от того, в какой точке его измеряют. В случае квазилинейной функции полезности компенсирующая вариация дохода, эквивалентная вариация дохода и изменение избытка потребителя дают одну и ту же меру денежной стоимости изменения цены.

 

ПРИМЕР: Компенсирующая и эквивалентная вариации дохода

 

Предположим, что потребитель имеет функцию полезности вида  . Первоначально ему заданы цены (1,1), и доход его равен 100. Затем цена товара 1 возрастает до 2. Каковы компенсирующая и эквивалентная вариации дохода?

Нам известно, что функции спроса для данной функции полезности Кобба-Дугласа    заданы формулами

                       

 

                      .

 

Воспользовавшись этими формулами, мы увидим, что спрос потребителя изменяется с    до  .

 

Рис. 14.5 Излишек производителя. Чистый излишек производителя есть площадь треугольника слева от кривой предложения на рис. А, а изменение излишка производителя есть площадь трапеции на рис. В.

 

Чтобы подсчитать компенсирующую вариацию дохода, мы спрашиваем, сколько денег понадобится потребителю, чтобы при ценах (2,1) его благосостояние было точно таким же, как и при потреблении набора (50,50)? Если цены равны (2,1) и потребитель имеет доход m, мы можем подставить эти значения в функцию спроса и найти, что в оптимуме потребитель выбрал бы набор (m/4,m/2). Приравняв полезность этого набора к полезности набора (50,50), мы получаем   

 

           .

 

Решив это уравнение для m, получаем

           .

 

Следовательно, потребителю потребовалось бы добавить примерно 141 — 100=41$ после изменения цены, чтобы его благосостояние стало точно таким же, как до изменения цены.

Чтобы подсчитать эквивалентную вариацию дохода, мы спрашиваем, сколько денег при ценах (1,1) потребовалось бы, чтобы благосостояние потребителя стало таким же, как если бы он потреблял набор (25,50). Обозначив эту сумму денег буквой m и следуя той же логике, что и ранее, получаем

 

     .

 

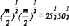Решив данное уравнение для m, получаем

 

            .

 

Таким образом, если бы потребитель при исходных ценах имел доход в 70 долл., его благосостояние было бы точно таким же, как при новых ценах и доходе в 100 долл. Эквивалентная вариация дохода составляет, следовательно,  примерно 100-70=30$.

 

ПРИМЕР: Компенсирующая и эквивалентная вариации дохода для случая квазилинейных предпочтений

 

Предположим, что потребитель имеет квазилинейную функцию полезности 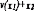 . Нам известно, что в этом случае спрос на товар 1 зависит только от цены товара 1, поэтому мы записываем его как  . Предположим, что цена меняется от   до  . Чему равны компенсирующая и эквивалентная вариации дохода?

При цене   потребитель выбирает   и имеет полезность  . При цене   потребитель выбирает   и имеет полезность  .

 

Пусть C — компенсирующая вариация дохода. Это — та дополнительная сумма денег, которая потребовалась бы потребителю после изменения цены, чтобы его благосостояние стало таким же, каким оно было до изменения цены. Приравняв эти полезности, мы получаем

 

    .

 

Решив это уравнение для C, получаем

 

    .

 

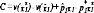Пусть E — эквивалентная вариация дохода. Это — та сумма денег, которую можно было бы отобрать у потребителя до изменения цены, чтобы оставить его с такой же  полезностью, которая будет у него после изменения цены. Следовательно, эта величина должна удовлетворять уравнению

 

    .

 

Решив это уравнение для E, мы получаем

 

    .

Обратите внимание на то, что в случае квазилинейной функции полезности компенсирующая и эквивалентная вариации дохода одинаковы. Более того, обе они равны изменению излишка потребителя (чистого):

 

   .

 

 

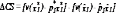Краткие выводы

 

1. В случае дискретного товара и квазилинейной функции полезности полезность, связываемая с потреблениемn единиц дискретного товара, есть просто сумма первых n резервных цен.

 

2. Эта сумма представляет собой валовую выручку от потребления данного товара. Вычтя из нее сумму, затраченную на покупку товара, мы получаем излишек потребителя.

 

3. Изменение излишка потребителя, связываемое с изменением цены, представлено площадью, по форме близкой к трапеции. Его можно трактовать как изменение полезности, связываемое с изменением цены.

 

4. В общем случае, для измерения в денежных единицах воздействия изменения цены на полезность можно использовать компенсирующую и эквивалентную вариации дохода.

 

5. При квазилинейной функции полезности компенсирующая вариация дохода, эквивалентная вариация дохода и изменение излишка потребителя равны между собой. Даже если функция полезности не является квазилинейной, изменение излишка потребителя может служить неплохой приблизительной мерой влияния изменения цены на полезность, получаемую потребителем.

 

6. При изучении поведения со стороны предложения мы можем определить излишек производителя как меру чистой выгоды для поставщика от производства данного объема продукции.

 

9. РЫНОЧНЫЙ СПРОС. Переход от индивидуального спроса к рыночному. Интенсивный и экстенсивный пределы. Эластичность, ее связь с выручкой. Кривая спроса неизменной эластичности. Эластичность и предельная выручка. Приложение: кривая Лаффера.

.