14.3 Другие интерпретации излишка потребителя

 

Существуют и другие подходы к интерпретации излишка потребителя.

Предположим, что цена дискретного товара равна p. Тогда потребитель оценивает потребление первой единицы этого товара в  , но должен заплатить за нее только p. Это дает ему "излишек" в размере   на первую единицу потребления. Вторую единицу потребления он оценивает в  , но снова должен заплатить за нее только p. Это дает ему излишек в размере   на данную единицу потребления. Если сложить подобные излишки по всем n единицам, на которые потребитель предъявляет спрос, мы получим его общий излишек потребителя:

 

.

 

 

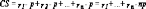Поскольку сумма резервных цен дает нам не что иное как полезность потребления товара 1, это выражение можно переписать также в виде

      CS=v(n)-pn

          

Излишек потребителя можно интерпретировать и по-другому. Предположим, что потребитель потребляет nединиц дискретного товара и платит за это pn долларов. Сколько денег потребовалось бы ему, чтобы вообще отказаться от потребления этого товара? Пусть требуемая для этого сумма есть R. Тогда R должна удовлетворять уравнению

      v(0)+m+R=v(n)+m-pn.

 

Поскольку v(0)=0 по определению, это уравнение сводится к

         R=v(n)-pn,

 

а это как раз и есть излишек потребителя. Следовательно, излишек потребителя показывает сумму, которую надо было бы заплатить потребителю, чтобы заставить его полностью отказаться от потребления какого-либо товара.

 

14.4 От излишка потребителя к излишку потребителей

 

До сих пор мы рассматривали случай единственного потребителя. Если речь идет о нескольких потребителях, мы можем сложить излишки потребителя для всех потребителей, получив такую совокупную меру, как излишек потребителей. Обратите внимание на различие этих двух понятий: понятие "излишек потребителя" относится к излишку для одного потребителя; понятие "излишек потребителей" относится к сумме излишков для ряда потребителей.

Излишек потребителей служит удобной мерой совокупных выгод от обмена, подобно тому, как излишек потребителя служит мерой выгод от обмена для отдельного индивида.

 

14.5 Как мы видели, площадь под кривой спроса на дискретный товар измеряет полезность потребления этого товара. Эту идею можно распространить на случай товара, приобретаемого в непрерывных количествах, если считать непрерывную кривую спроса приближением "лестничной" кривой спроса. Площадь под непрерывной кривой спроса оказывается в этом случае примерно равной площади под "лестничной" кривой спроса.

Пример этого можно увидеть на рис.14.1. В Приложении к настоящей главе мы показываем, как использовать дифференциальное исчисление для точного подсчета площади под кривой спроса.

 

14.7 Интерпретация изменения излишка потребителя

 

Абсолютная величина излишка потребителя, как правило, не слишком нас волнует.Обычно нас в большей степени интересует изменение излишка потребителя, являющееся результатом каких-то изменений экономической политики. Допустим, например, что цена товара изменяется с p' до p''. Как изменится при этом излишек потребителя?

На рис.14.3 мы проиллюстрировали изменение излишка потребителя, связанное с изменением цены. Изменение излишка потребителя есть разность двух площадей примерно треугольной формы и потому должно иметь примерную форму трапеции. Эта трапеция, в свою очередь, состоит из двух частей — прямоугольника, обозначенного 

буквой R, и фигуры, похожей на треугольник и обозначенной буквой T.

 

Рис.14.3 Изменение излишка потребителя. Изменение излишка потребителя представлено разностью двух площадей примерно треугольной формы и поэтому должно иметь примерную форму трапеции.

 

Площадь прямоугольника измеряет потерю излишка потребителя, вызванную тем фактом, что теперь потребитель платит больше за все единицы товара, которые он продолжает потреблять. После повышения цены потребитель продолжает потреблять   единиц товара, и каждая из этих единиц стала теперь дороже на  . Это означает, что просто для того, чтобы по-прежнему потреблять   единиц товара,  он должен израсходовать теперь денег на   больше, чем раньше.

Однако, потеря благосостояния к этому не сводится. Вследствие повышения цены товара x, потребитель решил потреблять его меньше, чем раньше. Площадь треугольника T измеряет стоимость потерянногопотребления товара x. Общая потеря для потребителя представлена суммой этих двух эффектов: R измеряет потерю, вызванную необходимостью платить за те единицы товара, которые он продолжает потреблять, а Tизмеряет потерю, вызванную сокращением потребления.

 

ПРИМЕР: Изменение излишка потребителя

 

Вопрос: Дана линейная кривая спроса D(p)=20-2p. Каково изменение излишка потребителя при изменении цены от 2 до 3?

 

Ответ: Когда p=2, D(2)=16, а когда p=3, D(3)=14. Таким образом, мы хотим подсчитать площадь трапеции с высотой 1 и основаниями 14 и 16. Она эквивалентна сумме площади прямоугольника с высотой 1 и основанием 14 (равной 14) и площади треугольника с высотой 1 и основанием 2 (равной 1). Общая площадь составит поэтому 15.