4. Формула площади четырехугольника, вокруг которого можно описать окружность

S = √

(

p - a

)(

p - b

)(

p - c

)(

p - d

)

Вы можете воспользоваться онлайн калькулятором для расчета площади четырехугольника.

Формулы площади круга

1. Ф ормула площади круга через радиус Площадь круга равна произведению квадрата радиуса на число пи.

S = 

π r

²

2. Формула площади круга через диаметр Площадь круга равна четверти произведения квадрата диаметра на число пи.

S =	1	π d 2
	4

где S - Площадь круга,

r

 - длина радиуса круга,

d

 - длина диаметра круга.

Вы можете воспользоваться онлайн калькулятором для расчета площади круга.

Формулы площади эллипса

П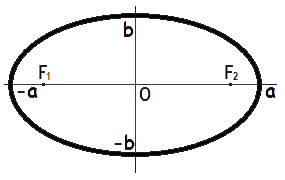 лощадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

S = 

π · a · b

где S - Площадь эллипса, 

a

 - длина большей полуоси эллипса, 

b

 - длина меньшей полуоси эллипса.

Площадь полной поверхности куба

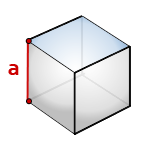
a - сторона куба

Формула площади поверхности куба, (S):

Найти площадь поверхности прямоугольного параллелепипеда

a, b, c,- стороны параллелепипеда

Формула площади поверхности параллелепипеда, (S):

Найти площадь поверхности шара, формула

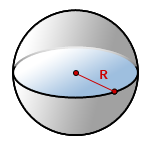
 R - радиус сферы

π ≈ 3.14

Формула площади поверхности шара (S):

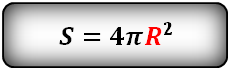
Площадь поверхности шарового сегмента

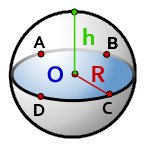
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R - радиус самого шара

h - высота сегмента

π ≈ 3.14

 Формула площади поверхности шарового сегмента,(S):

 

Площадь поверхности шарового слоя

h - высота шарового слоя, отрезок KN

R - радиус самого шара

O - центр шара

π ≈ 3.14

 Формула площади боковой поверхности шарового слоя, (S):

 

 Площадь поверхности шарового сектора

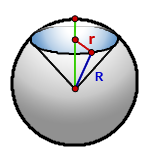
R - радиус шара

r - радиус основания конуса = радиус сегмента

π ≈ 3.14

 Формула площади поверхности шарового сектора, (S):

 

Расчет площади поверхности цилиндра

 r- радиус основания

h- высота цилиндра

π ≈ 3.14

Формула площади боковой поверхности цилиндра, (S_бок):

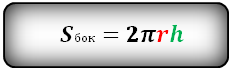
 Формула площади всей поверхности цилиндра, (S):

Площадь поверхности прямого, кругового конуса

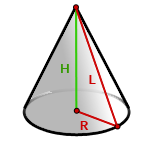
R - радиус основания конуса

H - высота

L - образующая конуса

π ≈ 3.14

 

 

Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (S_бок):

Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (S_бок):

 Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):

 Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):

Формулы площади поверхности усеченного конуса

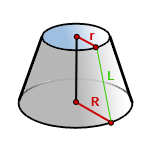
R - радиус нижнего основания

r- радиус верхнего основания

L - образующая усеченного конуса

π ≈ 3.14

 Формула площади боковой поверхности усеченного конуса, (S_бок):

 Формула площади полной поверхности усеченного конуса, (S):

 

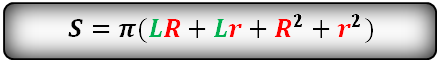
Площадь поверхности правильной пирамиды через апофему

L - апофема (опущенный перпендикуляр OC из вершины С, на ребро основания АВ)

P- периметр основания

S_осн - площадь основания

 Формула площади боковой поверхности правильной пирамиды (S_бок):

 Формула площади полной поверхности правильной пирамиды (S):

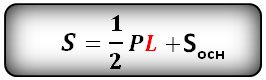
Площадь боковой поверхности правильной усеченной пирамиды

m - апофема пирамиды, отрезок OK

P - периметр нижнего основания, ABCDE

p - периметр верхнего основания, abcde

 Формула площади боковой поверхности правильной усеченной пирамиды, (S):

МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ. ПЛОЩАДЬ И ОБЪЕМ

 

ПЛОЩАДЬ ПЛОСКИХ ФИГУР

 

прямоугольник	S = a × b, где a, b - строны прямоугольника
треугольник	S = a × h/2, где a, h - строна и высота треугольника
параллелограмм	S = a × h, где a, h - строна и высота параллелограмма
трапеция	S = ( a + b ) h/2, где a, b - основания; h - высота трапеции
окружность	S = πR2, где R - радиус окружности
эллипс	S = π × a b, где a, b - большая и малая полуоси эллипса

 

ПЛОЩАДЬ ПОВЕРХНОСТИ ОБЪЕМНЫХ ФИГУР

 

параллепипед	S = 2(ab+bc+ac), где a, b, c - ребра параллепипеда
конус	S = πRl + πR2 , где R - радиус окружности; l - длина образующей
круговой цилиндр	S = 2πR(h+R) , где R - радиус окружности; h - высота
сфера (шар)	S = 4πR2 , где R - радиус сферы
тетраэдр	S = 1,7321 a2 , где а - ребро
октаэдр	S = 3,4641 a2 , где а - ребро
додекаэдр	S = 20,6457 a2 , где а - ребро
икосаэдр	S = 8,6603 a2 , где а - ребро

 

ОБЪЕМ ФИГУР

 

параллепипед	V = a × b × с, где a, b, c - ребра параллепипеда
конус	V = (1/3)πR2, где R - радиус окружности; h - высота
круговой цилиндр	V = πR2 × h , где R - радиус окружности; h - высота
сфера (шар)	V = (4/3)πR3 , где R - радиус сферы
эллипсоид	V = (4/3)πabc, где a, b, c - полуоси эллипса
тетраэдр	V = 0,1179 a3 , где а - ребро
октаэдр	V = 0,4714 a3 , где а - ребро
додекаэдр	V = 7,6631 a3 , где а - ребро
икосаэдр	V = 2,1817 a3 , где а - ребро