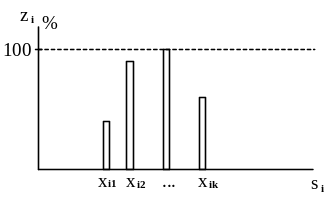Оцінка складних об єктів, вибір, класифікація (роспізнавання образів), формування висновку

Оцінювання завжди відбувається за наявністю об'єкта оцінки й суб'єкта оцінки. Суб'єкт оцінки формує певні вимоги V={v₁, v₂,..., v_l} до об'єкта, які, фактично, є вираженням мети оцінки. Об'єкт існує у вигляді множини своїх властивостей S={s₁, s₂, … , s_m}, які можуть бути як кількісними, так й якісними, і аналізуються відповідно до вимог суб'єкта.

Кожна властивість має множину своїх значень. Для кількісних властивостей – це значення з деякого діапазону X_і = [х_{і min}, x_{і max}], а для якісних – кінцева множина заздалегідь заданих значень X_і = {х_і1,…, x_ік}.

Сама по собі деяка властивість не може бути позитивна або негативна, її спрямованість проявляється тільки в рамках певної мети оцінювання, що може бути формалізована у вигляді множини вимог до об'єкта. Таким чином, повинна мати місце відповідність властивостей об'єкта пропонованим вимогам, тоді оцінка буде формуватися як міра відповідності (задоволення) між властивостями об'єкта й вимогами суб'єкта.

Розглянемо множину , що є декартовим добутком елементів множин V й S.

Для кожної конкретної задачі ОСО будемо формувати відображення

.

Стрілка спрямована від вимог до властивостей, указуючи на те, що вимоги є формальним описом мети.

Потужністю відображення F будемо називати кількість пар i=1..l, j=1..m (рис. 1.), і будемо позначати M(F) = n. При цьому в загальному випадку .

Для відображення F виконується наступна умова:

де – підмножина властивостей, поставлених у відповідність вимозі , тобто .

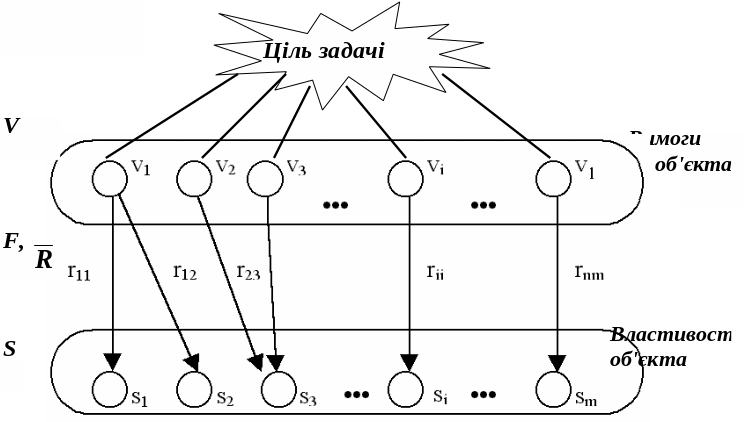
Рис. 1.1 - Компліментарна 2-рангова модель

Завдяки введенню відображення F можна задавати значення або діапазони значень відповідних властивостей, які максимально задовольняють вимогам.

Еталонними будемо називати такі значення властивостей, які задовольняють цілі проведеного оцінювання на 100%. Однак, для рішення задачі оцінки недостатньо знати тільки найкращий (або найгірший) об'єкт, – необхідно враховувати, як можливі значення деякої властивості впливають на далекість\наближеність об'єкта оцінки відносно еталона.

Цей вплив пропонується описувати у вигляді функції: z_i=f_i(x), xX_i, що визначена на всіх значеннях властивості і приймає значення від 0 до 100%, тобто вказує вплив всіх значень на підсумкову оцінку. Будемо називати функцією міри виразності (ФМВ) властивості . Залежно від умов кожної конкретної задачі ФМВ може формуватися або на підставі думки експертів, і тоді її можна інтерпретувати як функцію корисності, задану на множині значень конкретної властивості, або на базі навчальних вибірок, і тоді ФМВ може інтерпретуватися як функція розподілу ймовірностей значень властивості, або як функція приналежності, відома в теорії нечітких множин.

Тоді має місце твердження:

(3)

Це приводить до формування еталона оцінки, – об'єкта, всі властивості якого задовольняють всім вимогам на 100%:

оскільки (4)

де n – кількість пар «вимога – властивість» у відображенні F.

Еталону може відповідати реальний об'єкт або якийсь гіпотетичний “ідеал”, у кожному разі еталон задає точку відліку, щодо якої може бути зроблене кількісне оцінювання інших об'єктів.

Наведені положення показують обов'язковість існування еталона в будь-якій задачі оцінки. Якщо оцінка проводиться людиною-експертом, то еталон може бути не усвідомлений, не формалізований, але він є присутнім завжди.

Загальна оцінка об'єкта складається з його елементарних оцінок, визначених у рамках пари «вимога – властивість». Таким чином, якщо задано об'єкт оцінки , то для кожної пари «вимога – властивість» може бути обчислена елементарна міра відповідності

, j=1.. n, l=1.. m,

де – деяка функція, що залежить від способу урахування впливу різних елементарних мір відповідності, у найпростішому випадку .

де n – кількість пар «вимога – властивість» відображення F,

m – кількість властивостей об'єкта.

Тоді підсумкова оцінка об'єкта буде обчислюватися як:

, j=1 .. n,

де – деяка агрегуюча функція, що залежить від обраної метрики.

Таким чином, оцінку складних об'єктів пропонується робити в перетвореному просторі. Будемо називати його простором оцінки та позначати його Ŧ .

Оскільки ФМВ виражається у відсотках і не перевищує 100%, то цей простір є обмеженим – гіперпаралелепіпедом. Окремий випадок такого простору для n=3, і , зображений на рис. 2.

Тоді будемо називати кількісною оцінкою об'єкта його відстань до точки еталона в перетвореному n-мірному просторі, де n – кількість пар «вимога – властивість».

,

де – точка в перетвореному просторі, яка задана значеннями елементарних оцінок,

Е – точка еталона.

Ŧ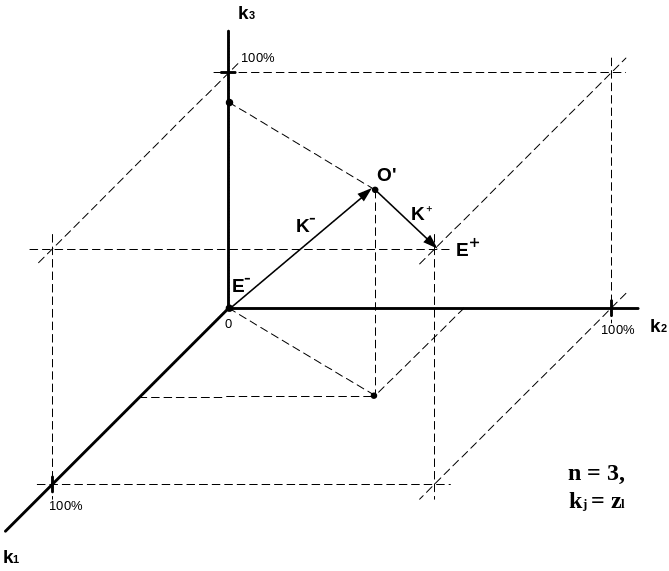

Рис. 1. 2 - Перетворений простір оцінки складних об'єктів

Запропонований підхід дозволяє формально описати й урахувати мету конкретної задачі оцінки, – вона відображається двома компонентами: списком вимог й описом еталона, відносно якого й оцінюються всі об'єкти. Вимоги дозволяють визначити мірність простору, а еталон – задає його розміри, габарити багатомірного прямокутного паралелепіпеда.

Різні задачі ІОІ відрізняються саме метою й типом одержуваного результату – символьним або кількісним. Зміни системи вимог й еталона дозволяють вирішувати різні задачі на базі запропонованого механізму оцінки складних об'єктів.

Крім того, показане (рис. 2), що в будь-якому просторі оцінки насправді існує два еталони – позитивний Е⁺ і негативний . Позитивний уже введений (3) і (4), аналогічно можна ввести негативний – це об'єкт, всі властивості якого відповідають всім вимогам на 0 %.

Фіксація двох еталонів Е⁺ й у явному виді повністю відповідає висновкам про обмеженість простору оцінки, і дозволяє уникнути однієї з досить розповсюджених помилок – устремління додатної, або від’ємної півосі оцінок у нескінченність. Інтервал значень оцінки, що задано еталонами, робить її не тільки конструктивною та наочною, але й дає можливість зробити оцінку “стереометричною”. Існує досить широкий клас задач, у яких оцінюється не тільки відстань до позитивного еталона, але також одночасно й відстань до негативного еталона.

Залежно від задачі обчислюються , , або пара ( , ). Без втрати загальності далі будемо використовувати К як характеристику близькості до еталона.

Різні вимоги по-різному впливають на процес оцінки в деякій задачі. Інакше кажучи, – вимоги мають різну значущість із погляду суб'єкта оцінки. Для урахування значимості вимог введемо вектор вагових коефіцієнтів.

Граничним випадком високої значимості деякої вимоги є ситуація, коли невідповідність об'єкта цій вимозі приводить до повністю незадовільної загальної оцінки об'єкта. Це означає, що у всій множині вимог можуть бути присутніми такі вимоги, невиконання яких не може бути скомпенсовано високим ступенем відповідності іншим вимогам. Такі вимоги будемо називати критичними. Для формального урахування фактору критичності введемо вектор бінарних коефіцієнтів C=(c₁, c₂, ..., c_l), де

Реалізація механізму критичних вимог дозволяє при необхідності додати оцінці «поріговий» характер, що відповідає змісту багатьох задач і значно підвищує адекватність формованих оцінок.

Якщо у відображенні F є вимоги, яким відповідають дві й більше властивості, то потрібен механізм урахування впливу властивостей, пов'язаних з однією вимогою. Для цього пропонується кожній з дуг «вимога – властивість» приписати коефіцієнт r_ij для урахування “міри відповідальності” j-ої властивості за виконання i-ї вимоги.

Як говорилося раніше, наявність відображення F дає можливість сформувати для кожного s_i його функцію міри виразності: z_i=f_i(x), що вказує вплив всіх значень s_i на підсумкову оцінку. ФМВ кількісних властивостей будуть безперервними (рис. 1.4а), а ФМВ якісних властивостей – дискретно-безперервними (рис. 1.4б).

а) б)

Рис. 1.4 - Еталони

Нехай = (z₁, z₂, ..., z_m) – вектор функцій міри виразності.

Отже, будемо вважати цілеорієнтовану компліментарну модель Мо процесу оцінки сформованою, якщо задано кортеж, що включає множину V і пов'язані з нею вектори и , множину S і вектор , а також відображення F з вектором дугових коефіцієнтів .

Інтегральною характеристикою (оцінкою) аналізованого об'єкта будемо називати величину K – міру близькості його опису, – точки в перетвореному просторі оцінки – до еталона.

Результатом рішення задачі кваліметрії є одне число – оцінка близькості об'єкта до еталона. У дискретно-безперервних просторах оцінку будемо обчислювати в такий спосіб:

У безперервних просторах пропонується обчислювати оцінку трохи інакше:

У ряді задач для сумірності оцінок доцільно нормувати величину К відносно К_maх, – гранично досяжного значення в даному просторі.

В задачі класифікації модель Mo повинна бути трохи розширена, й має наступний вигляд:

,

де T ={ t₁, t₂, ..., t_g } – множина розпізнаваних класів,

, , , – відповідно вектори вагових коефіцієнтів, дугових коефіцієнтів, коефіцієнтів критичності й функцій міри виразності, сформованих для кожного класу окремо.

Отже, для кожного класу, що треба розпізнавати, формується свій позитивний еталон. Аналізований об'єкт О_і=( х_і1, ... х_im ) послідовно розташовується в g просторів, які є просторами оцінки відповідних класів. У кожному просторі йому ставиться у відповідність точка О_і=( k_і1, ... k_in ), і від неї обчислюється відстань до точки-еталона даного простору. У такий спосіб:

Для об'єкта обчислюється стільки інтегральних характеристик, скільки є класів, що розрізняють. Ця множина інтегральних характеристик визначає ступінь близькості об'єкта до еталонів різних класів.

На підставі аналізу цієї множини інтегральних характеристик приймається рішення про приналежність об'єкта до одного з класів.

Вирішальне правило, що застосовується при цьому, має вигляд:

Далі запропонований формалізований об’єктно-орієнтований метод побудови цілеорієнтованой моделі процесу ОСО. Основні етапи цього методу представлені на рис. 1.5.

У випадку рішення задачі класифікації етапи II й III повинні бути виконані для кожного класу.

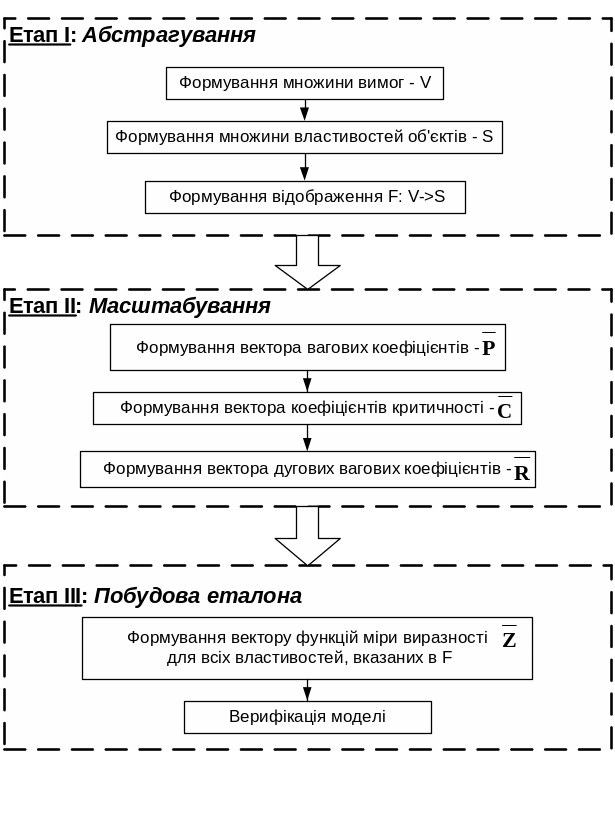
Рис. 1.5 - Основні етапи об’єктно-орієнтованого методу побудови цілеорієнтованой моделі процесу ОСО

Методики забезпечують два базових режими навчання: ручний – на базі знань людини-експерта, напівавтоматичний – на базі верифікованої статистики. Ці режими можуть використовуватися спільно, що істотно підвищує якість результату.