ОСНОВЫ ТЕОРИИ КОЛЕБАНИЙ:

Амплитуда и фаза вынужденных колебаний.

Амплитуда — максимальное отклонение колеблющейся величины от положения равновесия.

Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.

Амплитуду и начальную фаза колебания.

                                                                      (3)

.                                                                                          (4)

Величина   называется коэффициентом затухания, она определяется силой сопротивления среды и пропорциональна ее.

Амплитуда вынужденных колебаний зависит от амплитуды и вынуждающей силы и коэффициента затухания, и от того, насколько сильно эта частота отличается от собственной частоты.

Вращательные колебания. Критическое число оборотов.

Соответственно, для вращательного движения можно ввести величину, определяемую отношением изменения угловой скорости ко времени, в течение которого это изменение происходит – угловое ускорение: 

 Угловое ускорение показывает, на сколько изменилась угловая скорость за единицу времени.

Чтобы получить единицу углового ускорения, нужно в его определяющую формулу подставить единицы угловой скорости 1 рад/с и времени – 1 с. Получаем:

 

При вращении перемещению тела соответствует угол вращения, линейной скорости – угловая скорость, линейному ускорению – угловое ускорение, то аналогичное уравнение для вращательного движения будет иметь вид: 

Другому уравнению для поступательного движения  будет соответствовать уравнение для вращательного движения: 

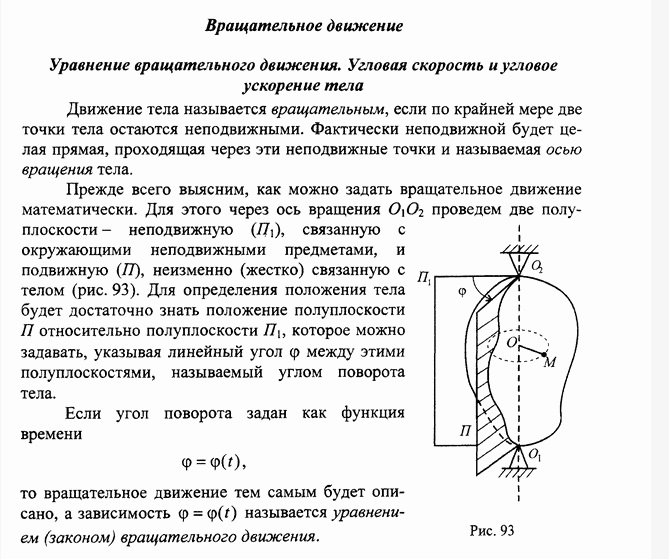
Вынужденные механические колебания под действием синусоидальной силы.

Если на колебательную систему действует периодически изменяющаяся внешняя сила, то система совершает колебания, характер которых в той или иной мере повторяет характер изменения этой силы. Такие колебания называются вынужденными. Установившиеся вынужденные колебания происходят с частотой, равной частоте вынуждающей силы.

Гармонические колебания и их характеристики. Векторная диаграмма.

Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид.

Гармоническими являются колебания, которые происходят под действием силы, пропорциональной смещению колеблющейся точки и направленной противоположно этому смещению.

или

,

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд;   — полная фаза колебаний,   — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

ХАРАКЕРИСТИКИ:

Если колебание описывать по закону косинуса

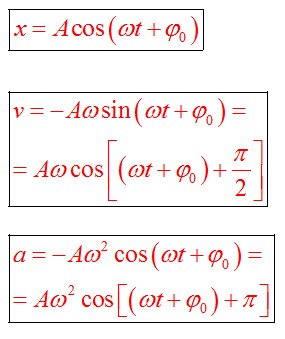
Если колебание описывать по закону синуса

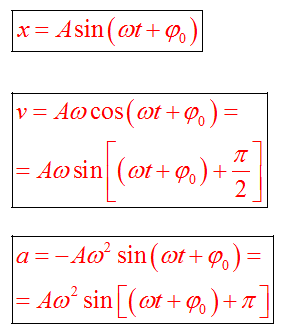
Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и так далее.

Гармоническое (то есть синусоидальное) колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постояннойугловой скоростью ω. Длина вектора соответствует амплитуде, угол поворота относительно оси (Ox) — фазе.

Сумма (или разность) двух и более колебаний на векторной диаграмме представлена при этом (геометрической) суммой^[1] (или разностью) векторов этих колебаний. Мгновенное значение искомой величины определяется при этом проекцией вектора суммы на ось Оx, амплитуда — длиной этого вектора, а фаза — углом его поворота относительно Ox.

Примеры применения - Механика; гармонический осциллятор

Гармонические осцилляторы: пружинный, математический и физический маятники.

Гармоническим осциллятором называется система, совершающая колебания, описы­ваемые уравнением вида (140.6):

Колебания гармонического осциллятора являются важным примером периодиче­ского движения и служат точной или при­ближенной моделью во многих задачах классической и квантовой физики. При­мерами гармонического осциллятора яв­ляются пружинный, физический и матема­тический маятники, колебательный контур (для токов и напряжений столь малых, что элементы контура можно было бы считать линейными; см. §146).

1. Пружинный маятник — это груз мас­сой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F=-kx, где k — коэффициент упругости, в случае пружины называемый жесткостью. Уравнение движения маятника

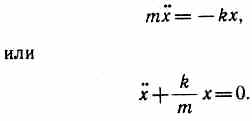
Формула (142.3) справедлива для упругих колебаний в пределах, в которых выпол­няется закон Гука т. е. когда масса пружины мала по сравнению с мас­сой тела.

Потенциальная энергия пружинного маятника, равна

П=kх²/2.

2. Физический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, не проходя­щей через центр масс тела (рис.201).

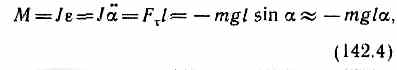
где У — момент инерции маятника относи­тельно оси, проходящей через точку О, l — расстояние между точкой подвеса и цент­ром масс маятника, F_=-mgsinmg — возвращающая сила (знак минус обусловлен тем, что направленияF_ и  всегда противоположны; sin соответствует малым колебаниям маятни­ка, т. е. малым отклонениям маятника из положения равновесия).

Уравнение    (142.4)    можно   записать в виде

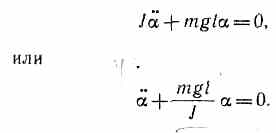
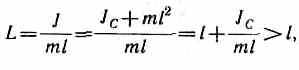
т. е. ОО' всегда больше ОС. Точка подвеса О и центр качаний О' обладают свойством взаимозаменяемости: если ось подвеса пе­ренести в центр качаний, то точка О пре­жней оси подвеса станет новым центром качаний и период колебаний физического маятника не изменится.

3, Математический маятник— это идеализированная система, состоящая из материальной точки массой т, подвешен­ной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тя­жести. Хорошим приближением математи­ческого маятника является небольшой тя­желый шарик, подвешенный на тонкой длинной нити.

Момент инерции математического маятника J=ml²,

где l — длина маятника.

Так как математический маятник мож­но представить как частный случай физи­ческого маятника, предположив, что вся его масса сосредоточена в одной точке — центре масс.