1. Назначение, примеры применения адаптивных фильтров: адаптивное шумоподавление, идентификация, линейное предсказание.

Адаптивный фильтр – разновидность цифрового фильтра, в которой коэффициенты фильтра изменяются в соответствии с некоторым критерием. Адаптивные фильтры применяются в том случае, когда статистические параметры обрабатываемого сигнала неизвестны или меняются со временем. При этом адаптивный фильтр автоматически подстраивается под изменяющиеся условия функционирования. Примеры применения адаптивных фильтров:

1. Адаптивное шумоподавление.

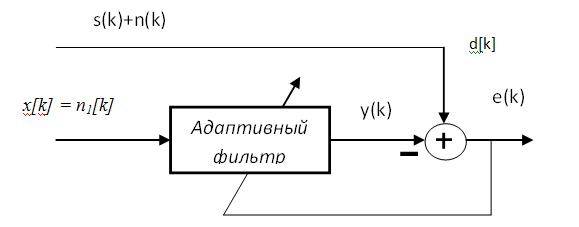
На основной вход фильтра подается сигнал помехи x[k] = n₁[k], на опорный вход - сумма d[k] = s[k]+n[k] полезного сигнала и помехи n[k], коррелированной с помехой n₁[k] на основном входе. Сигналы s[k] и x[k] должны быть не коррелированны друг с другом. В процессе адаптации адаптивный алгоритм настраивает коэффициенты фильтра таким образом, чтобы сигнал y[k], полученный из сигнала x[k], имел наилучшее приближение n[k]. В этом случае, при сигнал ошибки , т. е. после окончания настройки ошибка фильтра будет близка к полезному сигналу.

Примеры применения АФ в режиме шумоподавления: компенсация сетевой помехи, подавление ЭКГ матери в фетальной электрокардиографии, исключение ЭКГ-артефактов из сигнала ЭМГ, подавление помех в речевых сигналах и т. д.

2. Идентификация систем

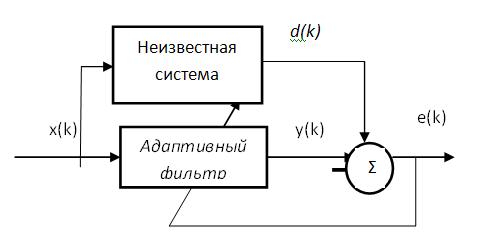
На вход неизвестной системы и адаптивного фильтра подается один и тот же сигнал. Адаптивный фильтр настраивается по минимуму среднеквадратичной ошибки таким образом, чтобы его выходной сигнал соответствовал выходному сигналу неизвестной системы. При этом передаточная функция адаптивного фильтра будет близка к передаточной функции неизвестной системы.

Примеры использования адаптивной идентификации систем: компенсация акустического эха, синтез цифровых КИХ-фильтров по эталону

3. Обратная идентификация систем

Адаптивный фильтр включается последовательно с исследуемой системой. В результате процесса адаптации сигнал на выходе адаптивного фильтра является приближением сигнала на входе неизвестной системы. При этом передаточная функция адаптивного фильтра будет близка к обратной передаточной функции неизвестной системы.

Примеры применения обратной идентификации систем: адаптивное выравнивание телефонных каналов, в системах управления для формирования сигналов управления.

4. Линейное предсказание

При линейном предсказании будущее значение входного сигнала оптимальным образом предсказывается по его прошлым значениям. При этом опорный сигнал – это входной сигнал s[k] в рассматриваемый момент времени, а входной сигнал АФ x[k] – это задержанный вход (прошлые значения s[k]). Путем настройки коэффициентов АФ стремится наиболее точным образом предсказать поведение сигнала x[k], используя значения ошибки предсказания e[k].

Применение: сокращение полосы частот речевых сообщений в мобильной связи.

2. Фильтр Винера

Фильтр Винера называется также линейным оптимальным фильтром, поскольку меньшее значение среднеквадратической ошибки, чем в фильтре Винера, в любом линейном фильтре получить нельзя

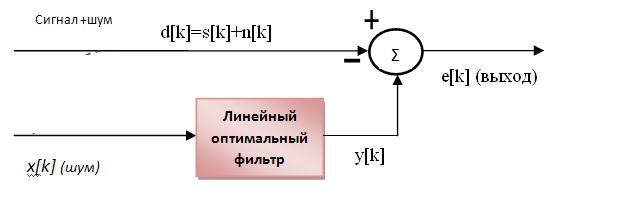
На вход фильтр поступают два сигнала: x[k] и d[k]. При этом d[k] содержит две составляющие – полезный сигнал s[k], который не коррелирован с x[k] и шумовую составляющую n[k], коррелированную с x[k]. Фильтр Винера должен иметь такую частотную характеристику, которая обеспечивает на выходе оптимальную в среднеквадратическом смысле оценку y[k] коррелированной части сигнала (шума) n[k]. Эта оценка вычитается из d[k] и выход (ошибка) фильтра e[k] – это наилучшая по среднеквадратическому критерию оценка полезного сигнала. Таким образом, фильтр Винера обеспечивает оптимальную оценку полезного сигнала, смешанного с аддитивным шумом, по критерию минимума среднеквадратической ошибки.

Предполагается, что фильтр является КИХ-фильтром с L-го порядка (с L коэффициентами). При этом его выход вычисляется как:

где вектор коэффициентов фильтра;

- вектор входного сигнала

Для оптимальной фильтрации необходимо найти оптимальный вектор коэффициентов W^*. Для этого необходимо найти функцию среднеквадратической ошибки, взять ее производную и приравнять к нулю:

;

;

;

- функция СКО

Чтобы удобнее представить функцию СКО, необходимо ввести следующие обозначения:

Эта матрица называется корреляционной матрицей входного сигнала. Элементы, расположенные на главной диагонали, равны среднеквадратическим значениям входных компонентов, а остальные элементы – значениям автокорреляционной функции входных компонентов.

Этот вектор представляет собой множество значений взаимной корреляционной функции полезного отклика и отсчетов входного сигнала.

Теперь можно записать:

Теперь, если взять производную от этой функции по W и приравнять ее к нулю, получим:

Это равенство называется уравнением Винера-Хопфа. Оно определяет вектор коэффициентов фильтра, обеспечивающий минимальное значение среднеквадратической ошибки оценки полезного сигнала в присутствии шума.

Несмотря на то, что этот фильтр является оптимальным, применение его на практике не слишком целесообразно ввиду очень большой вычислительной сложности. Количество операций типа «сложение-умножение» на итерацию у этого фильтра пропорционально третьей степени порядка фильтра. На практике обычно используют различные итеративные процедуры, сходящиеся к оптимальному фильтру.