
Вопросы с ответами к зачёту по математике для 10-х классов во втором полугодие 2013-2014 учебного года.
Числовая п., возрастающая, убывающая, ограниченная.
Определение предела числовой п.и, Т.ы о пределе суммы, произведения, частного сходящихся п.ей.
П.ю называется ф. от натурального аргумента.
П.
называется монотонно возрастающей
(строго возрастающей), если

 .
.
П.
называется монотонно убывающей (строго
убывающей), если
 .
.
Определение. Множество X действительных чисел (XR) называется ограниченным сверху, если существует действительное число С такое, что все элементы X не превосходят C.
 .
.
Замечание. Число С может принадлежать множеству X, а может и не принадлежать.
На числовой прямой все точки множества X, кроме точки С, если она принадлежит множеству X, лежат левее точки С.

Любое действительное число С, обладающее данным свойством, называют верхней гранью числового множества X.
Очевидно, что у любого ограниченного сверху множества бесконечное количество верхних граней.
Аналогично.
Определение. Множество X действительных чисел (XR) называется ограниченным снизу, если существует действительное число С1 такое, что все элементы X не меньше C1.
 .
.
Замечание. Число С1 может принадлежать множеству X, а может и не принадлежать.
На числовой прямой все точки множества X, кроме точки С1, если она принадлежит множеству X, лежат правее точки С1.

Любое действительное число С1, обладающее данным свойством, называют нижней гранью числового множества X.
Очевидно, что у любого ограниченного снизу множества бесконечное количество нижних граней.
Определение. Множество X действительных чисел (XR) называется ограниченным, если оно ограничено и сверху и снизу.
 .
.

Определение. Число M называется точной верхней гранью числового множества X, если выполняются следующие условия



Т.е. число М является наименьшим числом из множества верхних граней множества X.
Или словами: «Число М является верхней гранью множества X, и ни одно число меньшее М не является верхней гранью множества X».
Точная верхняя грань числового множества X обозначается supX (читается “супреум»).


 }
}
Определение. Число m называется точной нижней гранью числового множества X, если выполняются следующие условия
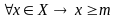

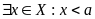
Т.е. число m является наибольшим числом из множества нижних граней множества X.
Или словами: «Число m является нижней гранью множества X, и ни одно число большее m не является нижней гранью множества X».
Точная нижняя грань числового множества X обозначается inf X (читается “инфимум»).

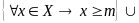
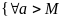 }
}
Замечание. Точная верхняя граница и точная нижняя граница могут принадлежать множеству X, а могут и не принадлежать.
На всех приведённых выше иллюстрациях в качестве верхней (нижней) границы приводились именно точные верхние (нижние) границы.
Число
А
называется пределом
п.и
 ,
если для любого сколь угодно малого
положительного числа
,
если для любого сколь угодно малого
положительного числа
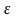 существует номер
существует номер
 ,
такой, что все значения
,
такой, что все значения
 ,
у которых
,
у которых
 ,
удовлетворяют неравенству
,
удовлетворяют неравенству
 .
Данное неравенство равносильно двойному
неравенству
.
Данное неравенство равносильно двойному
неравенству
 .
Геометрически это означает, что точки
,
начиная с некоторого номера
,
лежат внутри интервала
.
Геометрически это означает, что точки
,
начиная с некоторого номера
,
лежат внутри интервала
 ,
т.е. попадают в какую угодно малую
окрестность точки A.
,
т.е. попадают в какую угодно малую
окрестность точки A.
То,
что число А
является пределом
п.и
,
записывают так:
 .
.
На
языке кванторов определение предела
выглядит так:


 .
.
П., имеющая предел, называется сходящейся, в противном случае расходящейся.
Понятие предела существует только для п.ей содержащих бесконечное число членов.
Свойства пределов.
Т.а..
Если
и
 - п.и, и
- п.и, и
 ,
а
,
а
 ,
то
,
то
 .
.
Т.е.
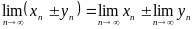
Док-во.
Пусть
 ,
а
,
а
 где
где
 и
и
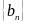 - бесконечно малые п.и.
- бесконечно малые п.и.
Тогда
 .
Т.к. А+В – константа, а
.
Т.к. А+В – константа, а
 - б.м., как сумма бесконечно малых, то п.
- б.м., как сумма бесконечно малых, то п.
 сходится к А+В.
сходится к А+В.
Аналогично
доказывается, что п.
 сходится к АВ.
сходится к АВ.
Т.а.
Если
и
- п.и, и
,
а
,
то
 .Т.е.
.Т.е.

Док-во.
Пусть , а где и - бесконечно малые п.и.
Тогда
 .
Т.к.
.
Т.к.
 –
константа, а
–
константа, а
 ,
,
 и
и
 - бесконечно малые, то п.
- бесконечно малые, то п.
 сходится к
.
сходится к
.
Т.а..
Если
и
- п.и, и
 ,
а
,
а
 ,
и начиная с некоторого номера N1,
,
и начиная с некоторого номера N1,
 ,
то
,
то
 .
Т.е.
.
Т.е.

Док-во.
Пусть
,
а
где
и
- бесконечно малые п.и
и начиная с некоторого номера N1
,
а начиная с некоторого номера N2
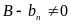 .
Пусть N
– наибольший из N1
и N2.
.
Пусть N
– наибольший из N1
и N2.
Тогда
начиная
с N
 .
Т.к.
и
.
Т.к.
и
 –
константы, а
,
,
и
–
константы, а
,
,
и
 - бесконечно малые п.и, то п.
- бесконечно малые п.и, то п.
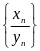 сходится к
сходится к
 .
.
Предел ф.и в точке по Гейне, по Коши; геометрический смысл предела ф.и в точке; Т.а о связи между ф.ей, ее пределом и б.м. ; Т.ы о пределах ф.й.
Понятие
предела ф.и является обобщением понятия
предела п.и, т.к. предел п.и можно
рассматривать как предел ф.и
 целочисленного аргумента n.
целочисленного аргумента n.
Пусть
дана ф.
 и пусть a
- предельная
точка
области определения этой ф.и (
и пусть a
- предельная
точка
области определения этой ф.и ( ),
т.е. такая точка, любая окрестность
которой содержит точки множества
,
отличные от a.
Точка a
может принадлежать множеству
,
а может и не принадлежать ему.
),
т.е. такая точка, любая окрестность
которой содержит точки множества
,
отличные от a.
Точка a
может принадлежать множеству
,
а может и не принадлежать ему.
Определение
1. Постоянное
число А называется пределом
ф.и
при
x
a,
если для всякой п.и
значений аргумента, стремящейся к а,
соответствующие им п.и
 имеют один и тот же предел А.
имеют один и тот же предел А.
Это определение называют определением предела ф.и по Гейне, или “ на языке п.ей ”.
Определение
2 .
Постоянное число А называется пределом
ф.и
при
x
a,
если, задав произвольное как угодно
малое положительное число
,
можно найти такое
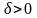 (зависящее от
),
что для всех x,
лежащих в
(зависящее от
),
что для всех x,
лежащих в

окрестности числа а,
т.е. для x,
удовлетворяющих неравенству
окрестности числа а,
т.е. для x,
удовлетворяющих неравенству
 ,
или
,
или
 ,
значения ф.и
будут лежать в
окрестности числа А, т.е. удовлетворять
неравенству
,
значения ф.и
будут лежать в
окрестности числа А, т.е. удовлетворять
неравенству
 , или
, или
 .
.
Это
определение называют определением
предела ф.и по Коши, или
“на
языке
 “.
“.
Определения
1 и 2 равносильны. Если ф.
при
x
a имеет предел, равный А, это записывается
в виде
 .
.
Определение через бесконечно малую.
Число A называется пределом ф.и f(x) при x , если существует б.м. (при x ) ф. a(x) такая, что f(x)=A+ a(x).
Т.а.
Если ф. y=f(x)
представима при x→
в
виде суммы постоянного числа b
и бесконечно малой величины α(x):
f (x)=b+ α(x)
то
 .
.
Обратно, если , то f (x)=b+α(x), где a(x) – б.м. при x→a.
Док-во.
1.
Из равенства f(x)=b+α(x)
следует |f(x)
– b|=|α(x)|.
Но т.к. a(x)
– б.м., то при произвольном ε найдется
такое значение M>0,
что при всех x,
таких, что |x|>M
значения a(x)
удовлетворяют неравенству |α(x)|<ε.
Тогда |f(x)
– b|<
ε. А это и значит, что
 .
.
2. Если , то значит, при любом ε>0 найдется такое значение M>0, что при всех x, таких, что |x|>M будет выполняться условие |f(x) – b|< ε. Если обозначить f(x) – b= α(x), то, при любом ε>0 для того же значения M, при всех x, таких, что |x|>M, будет выполняться условие |α(x)|<ε, а это значит, что α(x) – б.м., тогда f(x)=b+ (x), что и требовалось доказать.
Т.а о пределе суммы ф.й, имеющих предел при x .
Т.а. Предел суммы конечного числа ф.й при x , равен сумме пределов этих ф.й.
Док-во.
Проведем Док-во для двух слагаемых, т.к.
для любого конечного числа слагаемых
оно проводится так же. Пусть
 ,
а
,
а
 .Тогда
ф.и
и
.Тогда
ф.и
и
 могут быть представлены в виде f(x)=b+α(x)
и g(x)=c+β(x),
где α
и β
– бесконечно малые ф.и. Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
могут быть представлены в виде f(x)=b+α(x)
и g(x)=c+β(x),
где α
и β
– бесконечно малые ф.и. Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Т.к.
b
+ c есть
постоянная величина, а α(x)
+ β(x)
– ф. б.м., то
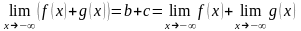
Аналогично доказывается Т.ы: «Предел суммы конечного числа ф.й при x +, равен сумме пределов этих ф.й» и «Предел суммы конечного числа ф.й при x , равен сумме пределов этих ф.й».
Т.а о пределе произведения ф.й, имеющих предел при x .
Т.а. Предел произведения конечного числа ф.й при x , равен произведению пределов этих ф.й.
Док-во.
Проведем Док-во для двух множителей,
т.к. для любого конечного числа множителей
оно проводится так же. Пусть
 ,
а
,
а
 .Тогда
ф.и
и
могут быть представлены в виде f(x)=b+α(x)
и g(x)=c+β(x),
где α
и β
– бесконечно малые ф.и.
.Тогда
ф.и
и
могут быть представлены в виде f(x)=b+α(x)
и g(x)=c+β(x),
где α
и β
– бесконечно малые ф.и.
Следовательно,
f(x)=b+α(x)
и g(x)=c+β(x)
и
 .
.
Произведение
bc
есть величина постоянная. Ф.
 на основании свойств бесконечно малых
ф.й есть величина б.м.. Поэтому
на основании свойств бесконечно малых
ф.й есть величина б.м.. Поэтому
 .
.
Аналогично доказывается Т.ы: «Предел произведения конечного числа ф.й при x +, равен произведению пределов этих ф.й» и «Предел произведения конечного числа ф.й при x, равен произведению пределов этих ф.й».
Т.а о пределе частного ф.й, имеющих предел при x +.
Т.а. Предел частного двух ф.й x + равен частному пределов этих ф.й, если предел знаменателя отличен от нуля, т.е.
Док-во.
Пусть
 и
и
 ,
причём c0.
Тогда ф.и
и
могут быть представлены в виде f(x)=b+α(x)
и g(x)=c+β(x),
где α
и β
– бесконечно малые ф.и.
,
причём c0.
Тогда ф.и
и
могут быть представлены в виде f(x)=b+α(x)
и g(x)=c+β(x),
где α
и β
– бесконечно малые ф.и.
Рассмотрим
частное
 =
=
Дробь
является бесконечно малой ф.ей, т.к.
числитель есть б.м. ф., а знаменатель
имеет предел c2≠0.
Поэтому,

Аналогично доказывается Т.ы: «Предел частного двух ф.й при x равен частному пределов этих ф.й, если предел знаменателя отличен от нуля» и «Предел частного двух ф.й при x равен частному пределов этих ф.й, если предел знаменателя отличен от нуля»
Т.а о пределе промежуточной ф.и; первый замечательный предел ф.и; второй замечательный предел ф.и.
Т.а.
Если
существует луч
 ,
на котором выполняются неравенства
,
на котором выполняются неравенства
 или
или
 ,
причём
,
причём
 ,
то
,
то
 .
.
Док-во.
Из
неравенств
и
следует, что при x>M
 .
.
Т.к.
,
то для любого
 найдётся M1>0,
что при всех x,
таких, что x>M1
будет выполняться условие |(x)
– b|<
ε.
найдётся M1>0,
что при всех x,
таких, что x>M1
будет выполняться условие |(x)
– b|<
ε.
Пусть М2 – большее из чисел М и М1. Тогда для любого x>M2 будет верно, что |(x) – b|< ε, а значит, будет верным и |f(x) – b|< ε, т.е. .
Определение односторонних пределов, предел ф.и при
 ;
Определение бесконечно большой ф.и;
определение бесконечно малой ф.и. Т.а
о сумме б.м.; о произведении ограниченной
ф.и на б.м.; о произведении б.м.; о
частном от деления б.м. на ф.ю, имеющую
предел
;
Определение бесконечно большой ф.и;
определение бесконечно малой ф.и. Т.а
о сумме б.м.; о произведении ограниченной
ф.и на б.м.; о произведении б.м.; о
частном от деления б.м. на ф.ю, имеющую
предел
 ;
Т.а о связи б.м. и б.б. ф.й.
;
Т.а о связи б.м. и б.б. ф.й.
Односторонние пределы.
Определение.
Постоянное число А называется левым
пределом
ф.и
при
x
a
(обозначается x
a0),
если, задав произвольное как угодно
малое положительное число
,
можно найти такое
(зависящее от
),
что для всех x,
лежащих в левой
окрестности числа а,
т.е. для x,
удовлетворяющих неравенству
 ,
значения ф.и
будут лежать в
окрестности числа А, т.е. удовлетворять
неравенству
, или
.
Записывают
,
значения ф.и
будут лежать в
окрестности числа А, т.е. удовлетворять
неравенству
, или
.
Записывают

Определение.
Постоянное число А называется правым
пределом
ф.и
при
x
a
(обозначается x
a+0),
если, задав произвольное как угодно
малое положительное число
,
можно найти такое
(зависящее от
),
что для всех x,
лежащих в правой
окрестности числа а,
т.е. для x,
удовлетворяющих неравенству
 ,
значения ф.и
будут лежать в
окрестности числа А, т.е. удовлетворять
неравенству
, или
.
,
значения ф.и
будут лежать в
окрестности числа А, т.е. удовлетворять
неравенству
, или
.
Записывают

Предел ф.и при x + и при x (через - окрестность).
Определение (через - окрестность).
Число A называется пределом ф.и f(x) при x , если для любого найдется такое M>0, что при |x |>M выполняется |f(x)A|< ε.
Число A называется пределом ф.и f(x) при x +, если для любого найдется такое M>0, что при x>M выполняется |f(x)A|< ε.
Число a называется пределом ф.и f(x) при x , если для любого найдется такое M>0, что при x<M выполняется |f(x)A|< ε.
Определение бесконечно большой ф.и.
Ф.
 называется бесконечно
большой
при x→a
если
для любого, сколь угодно большого числа
M>0 существует число
(зависящее от M),
что для всех x,
лежащих в
окрестности числа а,
т.е. для x,
удовлетворяющих неравенству
,
или
,
значения модуля ф.и
будут больше числа M, т.е. удовлетворять
неравенству
называется бесконечно
большой
при x→a
если
для любого, сколь угодно большого числа
M>0 существует число
(зависящее от M),
что для всех x,
лежащих в
окрестности числа а,
т.е. для x,
удовлетворяющих неравенству
,
или
,
значения модуля ф.и
будут больше числа M, т.е. удовлетворять
неравенству
 .
.
Ф.
называется бесконечно
большой
при x→∞
если
для любого, сколь угодно большого числа
M>0 существует число
 (зависящее от M),
что для всех x,
таких, что значение модуля x
больше N,
т.е. для x,
удовлетворяющих неравенству
(зависящее от M),
что для всех x,
таких, что значение модуля x
больше N,
т.е. для x,
удовлетворяющих неравенству
 ,
значения модуля ф.и
будут больше числа M, т.е. удовлетворять
неравенству
.
,
значения модуля ф.и
будут больше числа M, т.е. удовлетворять
неравенству
.
Если ф. является бесконечно большой при x→a если или при x→∞, то говорят, что предел ф.и в данной точке или на бесконечности равен бесконечности.
Записывают
так:
 или
или
 .
.
Ф.
называется бесконечно
малой
при x→a
если
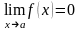 или
при x→∞,
если
или
при x→∞,
если
 ,
т.е. б.м. ф. – это ф., предел которой в
данной точке или на бесконечности равен
нулю.
,
т.е. б.м. ф. – это ф., предел которой в
данной точке или на бесконечности равен
нулю.
Свойство суммы и произведения бесконечно малых ф.й.
Т.а 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть ф. б.м..
Док-во. Проведем Док-во для двух слагаемых.
Пусть
 ,
где
,
где
 и
и
 .
Докажем, что при произвольном как угодно
малом
найдется
,
такое, что для x,
удовлетворяющих неравенству
,
выполняется
.
Докажем, что при произвольном как угодно
малом
найдется
,
такое, что для x,
удовлетворяющих неравенству
,
выполняется
 .
.
Т.
к. α(x)
– б.м. ф., то
 найдется
найдется
 такое, что при
такое, что при
 выполняется условие
выполняется условие
 .
Аналогично, т.к. β(x)
– б.м., то найдется такое
.
Аналогично, т.к. β(x)
– б.м., то найдется такое
 ,
что при
,
что при
 выполняется условие
выполняется условие
 .
.
Возьмем
 .Тогда
в δ
окрестности точки a
будет выполняться условие
.Тогда
в δ
окрестности точки a
будет выполняться условие
 ,
что и требовалось доказать.
,
что и требовалось доказать.
Т.а 2. Произведение бесконечно малой ф.и a(x) на ограниченную ф.ю f(x) при x→a (или при x→∞) есть б.м. ф..
Док-во
(при
x→a).
Т.к. ф. f(x)
ограничена, то существует число N
такое, что при всех значениях x
 .
Кроме того, т.к. a(x)
– б.м. ф. при x→a,
то для произвольного ε>0
найдется окрестность точки a,
в которой будет выполняться неравенство
.
Кроме того, т.к. a(x)
– б.м. ф. при x→a,
то для произвольного ε>0
найдется окрестность точки a,
в которой будет выполняться неравенство
 .
Тогда в этой окрестности имеем
.
Тогда в этой окрестности имеем
 .
А это и значит, что a(x)
f(x)
– б.м..
.
А это и значит, что a(x)
f(x)
– б.м..
Док-во
(при
x→∞).
Т.к. ф. f(x)
ограничена, то существует число N
такое, что при всех значениях x
 .
Кроме того, т.к. a(x)
– б.м. ф. при x→∞,
то для произвольного ε>0
найдется число M>0
такое, что выполняется неравенство
.
Тогда при
.
Кроме того, т.к. a(x)
– б.м. ф. при x→∞,
то для произвольного ε>0
найдется число M>0
такое, что выполняется неравенство
.
Тогда при
 имеем
.
А это и значит, что a(x)
f(x)
– б.м..
имеем
.
А это и значит, что a(x)
f(x)
– б.м..
Следствие 1. Произведение бесконечно малой ф.и и константы есть б.м. ф..
Следствие 2. Произведение конечного числа бесконечно малых ф.и есть б.м. ф..
Т.к. в некоторой окрестности точки a (при x→a), или при |x|M (при x→) б.м. f(x) является ограниченной.
Связь между бесконечно большой и бесконечно малой ф.ми.
Т.а.
Если ф.
- б.б., то ф.
 - б.м..
- б.м..
Док-во.
При

Выберем
произвольное
.
Т.к.
–
б.б., то для любого,
 (откуда
(откуда
 ),
найдется такое
,
что при
будет выполняться неравенство
.
Т.к. и
),
найдется такое
,
что при
будет выполняться неравенство
.
Т.к. и
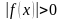 ,
и
,
и
 ,
и из
,
и из
 следует, что
следует, что
 ,
То при
будет выполняться условие
,
То при
будет выполняться условие
 что и требовалось доказать.
что и требовалось доказать.
Док-во.
При

Выберем произвольное . Т.к. – б.б., то для любого, (откуда ), найдется такое , что при будет выполняться неравенство . Т.к. и , и , и из следует, что , То при будет выполняться условие что и требовалось доказать.
ЗАМЕЧАНИЕ!!!
Обратное утверждение: «Если
ф.
- б.м., то ф.
- б.б.» справедливо только в том случае,
если существует такая окрестность точки
a,
в которой ф.
не обращается в 0 ни в одной точке (при
),
или существует такое число N, что при
всех x,
таких, что
,
 (при
)
(при
)
Непрерывность ф.и в точке, на отрезке, интервале. Точки разрыва и их классификация. Т.а о сумме ,произведении, частном двух непрерывных ф.й, Т.а о непрерывности сложной ф.и, обратной ф.и.
Рекомендую почитать
http://www.fizmatik.ru/index.php?option=com_content&view=article&id=15&Itemid=16
http://fmi.asf.ru/library/book/MatAn1/Glava3.html
Ф.
f(x)
непрерывна в точке a,
если
 .
Ф. непрерывна на интервале (A;B),
если она непрерывна в каждой точке этого
интервала. Ф. f(x)
непрерывна, если она непрерывна на все
область определения.
.
Ф. непрерывна на интервале (A;B),
если она непрерывна в каждой точке этого
интервала. Ф. f(x)
непрерывна, если она непрерывна на все
область определения.
Точка устранимого разрыва
Определение
Если
существуют левый
и правый пределы функции в точке
и они равны друг другу, но не совпадают
со значением функции
![]() в
точке
в
точке
![]() :
:
![]() или
функция
не
определена в точке
,
то точка
называется
точкой устранимого разрыва. #ОДЗ
можно пере- или доопределить.
или
функция
не
определена в точке
,
то точка
называется
точкой устранимого разрыва. #ОДЗ
можно пере- или доопределить.
Точка разрыва первого рода
Определение
Если
в точке
существуют
конечные пределы
![]() и
и
![]() ,
то точка
называется
точкой разрыва первого рода.
,
то точка
называется
точкой разрыва первого рода.
Точка разрыва второго рода
Определение
Если хотя б один из пределов или не существует или равен бесконечности, то точка называется точкой разрыва второго рода.
Теорема о сумме, разности, произведении и частном непрерывных функций
Теорема.
Пусть
![]() и
и
![]() непрерывны
в точке
непрерывны
в точке
![]() .
Тогда функции
.
Тогда функции
![]() ,
,
![]() и
и
![]() (в
последнем случае
(в
последнем случае
![]() )
также непрерывны в этой точке.Доказательство
следует из теоремы о пределах суммы,
разности, произведения и частного двух
функций.
)
также непрерывны в этой точке.Доказательство
следует из теоремы о пределах суммы,
разности, произведения и частного двух
функций.
Теорема о непрерывности сложной функции.
Пусть функция (t) непрерывна в точке t0 и функция f(x) непрерывна в точке х0=(t0). Тогда функция f((t)) непрерывна в точке t0.
Доказательство.
Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем

Выписывая подчеркнутые кванторы, получим, что
![]() ,
,
что и говорит о том, что f((t)) непрерывна в точке t0.
Обратите внимание на следующие детали:
а) т.к. x=(t), то |(t)-(t0)|< может быть записано как |x-x0|<, и f(x) превращается в F((t));
б)
при определении непрерывности (t)
в точке t0
в первом кванторе стоит буква .
Это необходимо для согласования с
квантором
![]() в
предыдущей строке и взаимного уничтожения
в
предыдущей строке и взаимного уничтожения
![]() .
Любая другая буква на этом месте не дала
бы верного результата.
.
Любая другая буква на этом месте не дала
бы верного результата.
Существование и непрерывность обратной функции. Теорема 1. Если функция y=f(x) строго возрастает (убывает) на множестве X, то для нее существует обратная функция x=f−1(y), которая определена на множестве Y=f(X) и является на Y строго возрастающей (убывающей). Доказательство. По условию функция f строго возрастает на множестве X. Это значит для любых x1,x2∈X и x1<x2 следует f(x1)<f(x2). Отсюда следует, что функция f обратима на X, следовательно, для нее существует обратная функция f−1:Y→X . Покажем, что функция f−1 строго возрастает на множестве Y. Пусть y1 и y2- любые точки из Y и y1<y2. Докажем, что x1=f−1(y1)<x2=f−1(y2). Допустим, чтоx1≥x2 . По условию функция f строго возрастает на X, поэтому из условия x1≥x2 вытекает неравенствоy1=f(x1)≥y2=f(x2) , что противоречит условию y1<y2. Т.о., условие строгой монотонности функции является достаточным для существования обратной функции.
Теорема 2. Если функция y=f(x) строго возрастает (убывает) и непрерывна на промежутке I, то существует обратная функция x=f−1(y), которая определена на промежутке Ef=f(I) и является на Е, строго возрастающей (убывающей) и непрерывной. Доказательство. Для определенности предположим, что функция f строго возрастает на промежутке I. По следствию из 2-ой теоремы Больцано-Коши область значений Ef=f(I) непрерывной функции f тоже есть промежуток. В силу строгого возрастания функции f для каждого y∈E существует единственная точка x∈I такая, что f(x)=y. Следовательно для функции f существует обратная функция f−1 определенная на промежутке Е и с множеством значений I.
Покажем, что f−1 строго возрастает на Е. Пусть y1 и y2-- две произвольные точки из Е, такие, что y1<y2 и прообразами этих точек будут точки x1и x2. f−1(y1)=x1, и f−1(y2)=x2.
Поскольку f - строго возрастающая функция, то неравенство y1=f(x1)<f(x2)=y2 возможно тогда и только тогда когда x1<x2 или тоже самое, когда f−1(y1)<f−1(y2). В силу произвольности y1 и y2 ∈E делаем вывод, что функция f−1 - строго возрастает на множестве Е. Что и требовалось доказать.
Определение производной, ее механический и геометрический смысл; уравнение касательной и нормали к кривой, Т.а о связи между непрерывностью и дифференцируемостью ф.и.
Про производную читайте в учебнике, стр.322-352.
Связь между дифференцируемостью и непрерывностью функции.
Докажем теорему, устанавливающую связь между дифференцируемостью и непрерывностью функции.
Теорема. Если функция y=f(x) дифференцируема в произвольной точке x0, то она непрерывна в этой точке.
Доказательство.
Пусть функция y=f(x) дифференцируема
в произвольной точке x0, т.е. имеет в этой
точке производную ![]() (x0).
Запишем приращение функции ∆y точке
x0:
(x0).
Запишем приращение функции ∆y точке
x0:
∆y
=
(x0)
∆ x +![]() ∆
x, где
→0 при ∆
x→0 (см. доказательство теоремы 6.1).
∆
x, где
→0 при ∆
x→0 (см. доказательство теоремы 6.1).
Пусть теперь ∆ x→0. Тогда, очевидно, и ∆y→0. Но это и означает, что функция y=f(x) непрерывна в точке x0. Теорема доказана.
Утверждение, обратное этой теореме, неверно: из непрерывности функции в данной точке не вытекает её дифференцируемость в этой точке. Существуют функции, непрерывные в некоторой точке, но не имеющие в этой точке производной. Примером такой функции служит функция
y=![]() =
=
Т.а о производной суммы, разности, произведения, частного ф.й, о производной сложной и обратной ф.и.
Про производную читайте в учебнике, стр.322-352.
Производные элементарных ф.й (степенной, тригонометрических, обратных тригонометрических ф.й).
Про производную читайте в учебнике, стр.322-352.
Т.ы Ролля, Коши, Лагранжа.
Теорема Ролля (о корнях производной):
Пусть
функция
![]() непрерывна
на
непрерывна
на
![]() и
дифференцируема на
и
дифференцируема на
![]() и
на концах отрезка принимает одинаковые
значения:
и
на концах отрезка принимает одинаковые
значения:
![]() .
Тогда существует хотя бы одна точка
.
Тогда существует хотя бы одна точка
![]() из
,
производная в которой
из
,
производная в которой
![]() .
.
Доказательство:
Непрерывная достигает на M и m. Тогда возможны два случая:
1)![]() ,
=>f(x)=const
=>
,
=>f(x)=const
=>![]()
2)
![]() наибольшее
значение достигается внутри интервала
наибольшее
значение достигается внутри интервала
![]() по
теореме Ферма.
по
теореме Ферма.
Теорема Лангража (о конечных приращениях):
П усть функция непрерывна на и дифференцируема на . Тогда существует хотя бы одна из , для которой выполняется следующее равенство:
![]() .
.
Доказательство:
Введем
функцию
![]() .
(непрерывная на
и
дифференцируемая на
).
.
(непрерывная на
и
дифференцируемая на
).
![]()
![]()
![]()
![]()
![]() ,
,![]()
Функция
![]() удовлетворяет
Теореме Ролля
удовлетворяет
Теореме Ролля
![]() существует
существует
![]() ,
для которой:
,
для которой:
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Теорема Коши:
Пусть
функции
и
![]() непрерывны
на
и
дифференцируемы на
,
непрерывны
на
и
дифференцируемы на
,
![]() на
.
Тогда существует хотя бы одна внутренняя
точка
,
для которой выполняется равенство
на
.
Тогда существует хотя бы одна внутренняя
точка
,
для которой выполняется равенство
![]() .
.
Доказательство:
Введем
функцию
![]() .
(непрерывная на
и
дифференцируемая на
).
.
(непрерывная на
и
дифференцируемая на
).
![]()
![]()
![]()
Функция
удовлетворяет
Теореме Ролля
существует
,
для которой:
,
![]() ,
,![]() ,
,![]() .
.
Необходимое условие возрастания (убывания) ф.и, достаточное условие возрастания(убывания) ф.и.
