Достаточное условие экстремума
Теорема. Пусть функция f (x) непрерывна в некотором интервале, содержащую точку экстремума х1, и дифференцируема во всех точках этого интервала кроме, быть может самой точки х1. Если при переходе слева направо через эту точку х1 производная меняет знак с плюса на минус, то при х = х1 функция имеет локальный максимум. Если же при переходе слева направо через эту точку х1 производная меняет знак с минуса на плюс, то функция имеет в этой точке локальный минимум. Комментарий. Если в достаточно малой окрестности точки х1 справедливо f ' (x) > 0 при х < x1, f ' (x) < 0 при х > x1, то в точке х1 функция имеет максимум; если f ' (x) < 0 при х < x1, f ' (x) > 0 при х > x1, то в точке х1 функция имеет минимум. Доказательство. Пусть при переходе слева направо через эту точку х1 производная меняет знак с плюса на минус, то есть для всех х, достаточно близких к х1, имеем f ' (x) > 0 при х < x1, f ' (x) < 0 при х > x1. Применяя теорему Лагранжа к разности f (x) − f ( x1), получим
f ( x ) − f ( x1 ) = f ' ( c )·( x − x1 ).
где с лежит между точками х и х1. По условию теоремы
sign f ' ( c ) = − sign ( x − x1 ),
поэтому в произвольно малой окрестности точки х1 имеем
f ( x ) < f ( x1 ).
В этом случае точка х1 есть точка локального максимума, что и требовалось доказать.
Наибольшее и наименьшее значение ф.и на отрезке, асимптоты ф.и, нахождение наклонных асимптот, общая схема исследования ф.й.
Выпуклость и вогнутость ф.и, точки перегиба, Т.а об интервалах выпуклости и вогнутости ф.и, достаточное условие существования точек перегиба.
Признак перпендикулярности плоскостей.
Т.а о трех перпендикулярах.
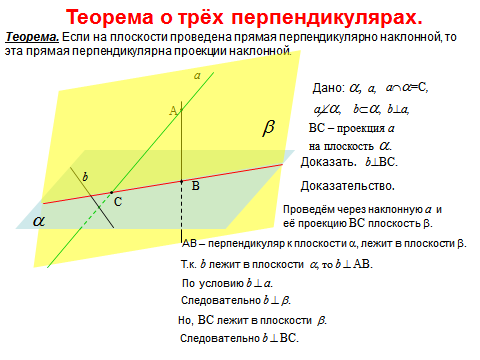
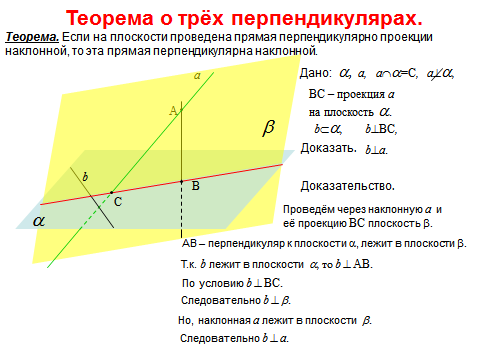
Признак перпендикулярности прямой и плоскости.
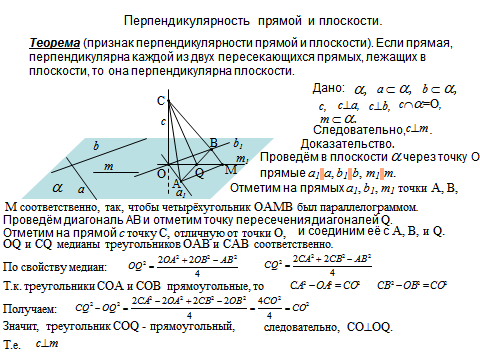
Если две прямые перпендикулярны плоскости, то они параллельны.
Если одна из двух параллельных прямых перпендикулярна плоскости, то и вторая перпендикулярна этой плоскости.
Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна их линии пересечения .
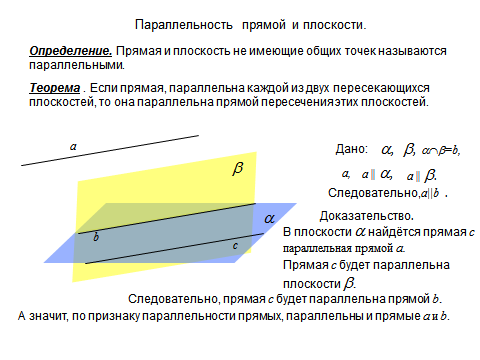
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны
Расстояние между скрещивающимися прямыми (в координатной форме)
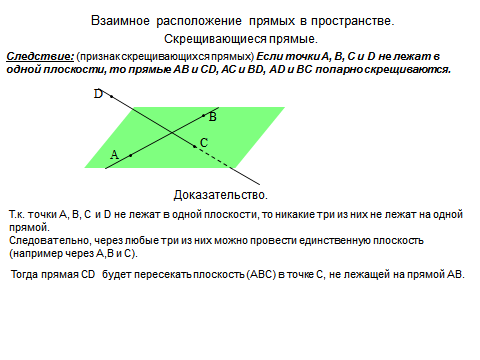
Признак скрещивающихся прямых.
Признак параллельности прямой и плоскости.
Аксиомы стереометрии. Доказать, что через две пересекающиеся прямые проходит плоскость, и притом только одна.
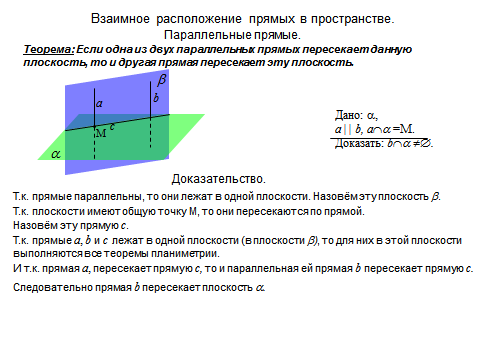
Если одна из двух параллельных прямых пересекает данную плоскость, то и вторая прямая пересекает эту плоскость.
Если две прямые параллельны третьей, то они параллельны друг другу.
Признак параллельности плоскостей.
Отрезки параллельных прямых, заключенные между параллельными плоскостями ,равны.
Векторное произведение векторов и его свойства. Векторное произведение в координатах.
Смешанное произведение векторов и его свойства. Смешанное произведение в координатах.
Общее уравнение плоскости, уравнение плоскости, заданной точкой и двумя неколлинеарными векторами; тремя точками.
Каноническое уравнение прямой в пространстве; уравнение прямой, заданной 2-мя точками; расстояние от точки до прямой, от точки до плоскости.
Скалярное произведение векторов. Вычисление угла между прямой и плоскостью, между плоскостями (в координатной форме).
Координаты вектора. Длина вектора. Линейные операции с векторами в координатах.
Единственность разложение вектора по трем неколлинеарным векторам.
Определение вектора в пространстве. Равные, коллинеарные, компланарные векторы. Линейные операции с векторами в пространстве.