Вопросы с ответами к зачёту по математике для 10-х классов во втором полугодие 2013-2014 учебного года.

1. Числовая п., возрастающая, убывающая, ограниченная.

Определение предела числовой п.и, Т.ы о пределе суммы, произведения, частного сходящихся п.ей.

П.Ю называется ф. От натурального аргумента.

П. называется монотонно возрастающей (строго возрастающей), если  .

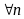
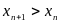П. называется монотонно убывающей (строго убывающей), если  .

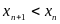Определение. Множество X действительных чисел (XR) называется ограниченным сверху, если существует действительное число С такое, что все элементы X не превосходят C.

.

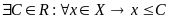Замечание. Число С может принадлежать множеству X, а может и не принадлежать.

На числовой прямой все точки множества X, кроме точки С, если она принадлежит множеству X, лежат левее точки С.

Любое действительное число С, обладающее данным свойством, называют верхней гранью числового множества X.

Очевидно, что у любого ограниченного сверху множества бесконечное количество верхних граней.

Аналогично.

Определение. Множество X действительных чисел (XR) называется ограниченным снизу, если существует действительное число С₁ такое, что все элементы X не меньше C₁.

.

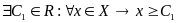Замечание. Число С₁ может принадлежать множеству X, а может и не принадлежать.

На числовой прямой все точки множества X, кроме точки С₁, если она принадлежит множеству X, лежат правее точки С₁.

Любое действительное число С₁, обладающее данным свойством, называют нижней гранью числового множества X.

Очевидно, что у любого ограниченного снизу множества бесконечное количество нижних граней.

Определение. Множество X действительных чисел (XR) называется ограниченным, если оно ограничено и сверху и снизу.

.

Определение. Число M называется точной верхней гранью числового множества X, если выполняются следующие условия

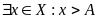
Т.е. число М является наименьшим числом из множества верхних граней множества X.

Или словами: «Число М является верхней гранью множества X, и ни одно число меньшее М не является верхней гранью множества X».

Точная верхняя грань числового множества X обозначается supX (читается “супреум»).

 }

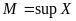
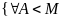Определение. Число m называется точной нижней гранью числового множества X, если выполняются следующие условия

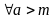
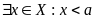
Т.е. число m является наибольшим числом из множества нижних граней множества X.

Или словами: «Число m является нижней гранью множества X, и ни одно число большее m не является нижней гранью множества X».

Точная нижняя грань числового множества X обозначается inf X (читается “инфимум»).

 }

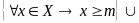
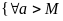Замечание. Точная верхняя граница и точная нижняя граница могут принадлежать множеству X, а могут и не принадлежать.

На всех приведённых выше иллюстрациях в качестве верхней (нижней) границы приводились именно точные верхние (нижние) границы.

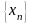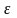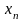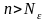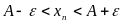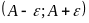Число А называется пределом п.и , если для любого сколь угодно малого положительного числа существует номер , такой, что все значения _, у которых , удовлетворяют неравенству . Данное неравенство равносильно двойному неравенству . Геометрически это означает, что точки , начиная с некоторого номера , лежат внутри интервала , т.е. попадают в какую угодно малую  окрестность точки A.

То, что число А является пределом п.и , записывают так: .

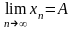На языке кванторов определение предела выглядит так: .

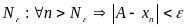П., имеющая предел, называется сходящейся, в противном случае  расходящейся.

Понятие предела существует только для п.ей содержащих бесконечное число членов.