26. Методика ознайомлення з письмовим множенням і діленням на одноцифрове число, в темі "Тисяча".

Письмове множення на одноцифрове число. Послідовність розгляду випадків множення визначається зростанням їх складності: 213 • 3 = 639 (множення без переходу через розряд); 37 • 6 = 222, 127 • 3 = 381 (множення з переходом через розряд); 151 • 6 = 906 (у добутку нуль); 125 • 4 = 500 (у добутку два нулі). І потім учні вчаться застосовувати набуті вміння для обчислення виразів на сумісні дії. Перехід від усного множення до письмового треба здійснити так, щоб учні усвідомили необхідність вивчення письмового множення (з цією метою учням потрібно запропонувати текстову задачу практичного змісту). Пояснення. При письмовому множенні другий множник записуємо під першим. Розмістити числа треба так, щоб одиниці другого множника були шписані під одиницями першого. Наприклад, 312 помножити на 3. При письмовому множенні починають множити з одиниць: множимо на 3 спочатку 2 од., потім 1 дес. і, нарешті, 3 сот. 2 од. помножити на 3, буде 6 од. Пишемо цифру 6 під одиницями. 1 дес. помножити на 3, буде 3 дес. Пишемо цифру 3 під десятками. З сот. помножити на 3, буде 9 сот. Пишемо цифру 9 на місці сотень. У добутку отримали число 936. Від докладного пояснення обчислення виразів такого виду учні переходять до короткого пояснення. Наприклад, докладне пояснення: 39 • 6 =234. Множимо 9 од. на 6, буде 54 од. Це 5 дес. і 4 од.; 4 од. пишемо під одиницями, а 5 дес. запам'ятовуємо; 3 дес. помножити на 6, буде 18 дес. та ще 5 дес, буде 23 дес. Це 2 сот. і 3 дес. Отримаємо 234. Коротке пояснення: 127• 3 =381 Множимо 7 на 3, буде 21; 1 пишемо, а 2 запам'ятовуємо; 2 множимо на 3, буде 6 та ще 2, буде 8. 1 помножити на 3, буде 3. Пишемо 3. Всього маємо 381. Письмове ділення на одноцифрове число. Алгоритм письмового ділення складається з багатьох операцій: перетворення одиниць вищого розряду на одиниці нижчого розряду, табличне ділення, ділення з остачею, множення, віднімання. Ці операції мають стати предметом підготовчої роботи. Велику увагу слід приділити повторенню випадків ділення з одиницею і нулем, перевірці ділення множенням. Випадок виду 966 : 3 розглядають без детального коментування; туї' головною є форма запису, розміщення компонентів письмового ділення. На наступному уроці подається детальне коментування ділення виду 864 : 4. При усному діленні ми розкладали ділене на зручні доданки і потім ділили на 3 кожний доданок окремо. При письмовому діленні також розкладають ділене на зручні доданки. Проте спочатку знаходять неповні ділені — цс числа, які попередньо виділяють із діленого, щоб відшукати цифру частки. Розгляньмо детальне пояснення процесу ділення на прикладі 276 : 4=69. Докладне пояснення. Ділене — 276, дільник — 4. Утворюємо перше неповне ділене. Вищий розряд діленого — сотні. 2 сот. не можна поділити на 4 так, щоб у результаті отримати сотні. Замінимо 2 сот. десятками і додамо 7 дес, отримаємо 27 дес. Це перше неповне ділене. Отже, вищий розряд частки — десятки. У частці буде дві цифри. Позначимо їх місце крапками. 27 дес. поділимо на 4, буде 6 дес. Запишемо цифру 6 у частці на місці десятків. Визначимо, скільки всього десятків поділили. Помножимо 6 дес. на 4, буде 24 дес. Запишемо 24 дес під 27 дес. діленого, тобто під першим неповним діленим і підведемо риску. Віднімемо 24 дес. від 27 дес, буде 3 дес; 3 дес. не можна поділити на 4 так, щоб отримати десятки. Отже, цифру 6 знайдено правильно. Утворимо друге неповне ділене. До остачі додамо 6 од. діленого; 3 дес. і 6 од., буде 36 од. Поділимо 36 од. на 4, буде 9 од. Запишемо цифру 9 у частці ми місці одиниць. Визначимо, скільки одиниць поділили. Помножимо 9 од. на 4, буде 36 од. Запишемо 36 од. під другим неповним діленим і підведемо риску. Віднімемо 36 від 36, буде 0. Одиниці поділили всі. Частка — 69. Наведений зразок пояснень свідчать про складність алгоритму письмового ділення. Засвоєння його викликає в учнів значні труднощі. Певну допомогу її їх подоланні може надати така пам 'ятка письмового ділення: 1. Виділіть перше неповне ділене і встановіть кількість цифр у частці. 2. Знайдіть першу цифру частки, дізнайтеся, скільки одиниць першого неповного діленого поділили і скільки залишилось поділити. 3. Утворіть друге неповне ділене і продовжуйте ділення, поки не розв'яжете приклад до кінця.

27. Методика вивчення усних та письмових прийомі додавання та віднімання багатоцифрових чисел. Учні вже знайомі з письмовим додаванням і відніманням трицифрових чисел, тому ознайомлення з діями в межах мільйона відбувається прямим перенесенням. Пропонують перевірити правильність розв’язання двох прикладів:

Учні повторно розв’язують приклади, пояснюють, як треба записувати числа при письмовому додаванні або відніманні. Після цього вчитель повідомляє, що письмове додавання і віднімання багатоцифрових чисел виконують так само, як додавання і віднімання трицифрових чисел. Далі учні виконують фронтально чи самостійно різні вправи на застосування дій першого ступеня: обчислення числових виразів з буквеними компонентами; розв’язування рівнянь та різних простих і складених задач. Перевірка віднімання додаванням. Учитель записує на дошці дві рівності: , .Учні повинні на числових прикладах обґрунтовувати, чому друга рівність буде правильною. Потім учитель повідомляє: якщо додати різницю і від’ємник, то дістанемо зменшуване. Цей зв’язок використовують для перевірки правильності виконання дії віднімання. У процесі розв’язування прикладів з коментуванням пояснюють обчислення різниці, коли у зменшуваному є кілька нулів; додавання кількох доданків; знаходження значень виразів  на сумісні дії першого ступеня та виразів з дужками. Наведемо один із зразків такого коментування. Треба від числа 3005 відняти 1126. Від 5 одиниць відняти 6 одиниць не можна. Оскільки у розрядах десятків і сотень 0 одиниць, то візьмемо 1 тисячу. Щоб не забути про це, у розряді тисяч поставимо крапку. Одна тисяча - це 10 сотень.9 сотень залишимо у розряді сотень, а одну сотню перетворимо у десятки. Одна сотня - це 10 десятків, 9 десятків залишимо в розряді десятків, а один десяток перетворимо в одиниці.1 десяток - це 10 одиниць. Та ще 5 одиниць, буде 15 одиниць. Від 15 одиниць відняти 6 одиниць, буде 9 одиниць. Пишемо 9 на місці одиниць. Від 9 десятків відняти 2 десятка, буде 7 десятків. Пишемо 7 на місці десятків. Від 9 сотень відняти 1 сотню, буде 8 сотень. Пишемо 8 на місці сотень. Від 2 тисяч відняти 1 тисячу, буде 1 тисяча. На місці тисяч пишемо 1. Різниця дорівнює 1879.

28. Методика вивчення усних та письмових прийомів множення багатоцифрових чисел на одноцифрове число.Відповідно до програми розглядають такі питання: поняття дії множення, переставний і сполучний закони дії і множення, розподільний закон множення відносно додавання, загальний випадок множення і особливі випадки множення, множення одноцифрового числа на багатоцифрове, множення іменованих чисел. Множення — особливий вид додавання: додавання однакових доданків. Помножимо чотирицифрове число 2 317 на 4 спочатку усно. Розкладемо це число на розрядні доданки і будемо множити за правилом множення суми на число.(2 000 + 300 + 10 + 7) • 4 = 8 000 + 1 + 200 + 40 + 28 = 9 268.

Усно знайти добуток можна, але без запису проміжних результатів зробити це важкувато. Треба в пам'яті одразу тримати багато чисел. Великі числа краще множити письмово, у стовпчик. Послухайте докладне пояснення. Треба помножити 2317 на 4. Записуємо другий множник під одиницями першого. Підводимо риску. Зліва ставимо знак множення "х". Розпочинаємо письмове множення з одиниць. Множимо 7 од. на 4, буде 28 од. Це 2 дес. і 8 од.; 8 од. пишемо під одиницями, а 2 дес. запам'ятовуємо. 1 дес. помножити на 4, буде 4 дес. та ще 2 дес, буде 6 дес. Пишемо їх під десятками. З сот. множимо на 4, буде 12 сот. Це 1 тис. і 2 сот.; 2 сот. пишемо під сотнями, а 1 тис. запам'ятовуємо.2 тис. помножити на 4, буде 8 тис. та ще 1 тис, буде 9 тис. Пишемо їх на місці тисяч. Добуток 9 268. На цьому ж записі подаємо зразок короткого пояснення: треба помножити 2 317 на 4. 7 на 4, буде 28. 8 пишемо, а 2 запам'ятовуємо. 1 на 4, буде 4 та ще 2, буде 6. З на 4, буде 12, 2 пишемо, а 1 запам'ятовуємо. 2 на 4, буде 8 та ще 1, буде 9. Добуток 9 268. При короткому поясненні опускаємо назви розрядних одиниць і міркування про перетворення проміжних результатів.

29. Методика вивчення усних та письмових прийомів ділення багатоцифрових чисел на одноцифрове число. Перед вивченням ділення багатоцифрового числа на одноцифрове узагальнюють поняття про дію ділення та її властивості. Діленням називається дія, за допомогою якої за добутком двох множників і одним із цих множників знаходять інший множник. 80 • 3 = 240 240 : 3 = 80. Число 240 називається діленим, 3 — дільником, 80 — часткою. У множині натуральних чисел дія ділення не завжди виконується. Наприклад, щоб поділити 50 на 6, треба знайти таке число х, для якого: 6 • х — 50. Такого натурального числа не існує, бо 6 • 8 = 48, а 6 • 9 = 54. Ділене 2 148, дільник 4. Перше неповне ділене 21 сот., тому в частці отримаємо трицифрове число. 21 поділимо на 4, буде 5. Поділили 20 сот. Залишилася 1 сот. Друге неповне ділене 14 дес. Поділимо на 4, буде 3 дес. Поділили 12 дес. Залишилося 2 дес. Третє неповне ділене 28 од. Поділимо на 4, буде 7 од. Частка 537. Слід звернути особливу увагу на випадки ділення, коли в результаті отримуємо нулі в кінці або всередині частки. Щоб учні не пропускали нулі в частці, треба привчити їх ще до виконання ділення за назвою першого неповного діленого визначати кількість цифр у частці.

30. Методика вивчення усних і письмових прийомів множення і ділення круглих чисел у 'темі "Багатоцифрові числа". Прийоми множення і ділення багатоцифрових чисел дуже різні і значно складніші, ніж прийоми + і - багатоцифрових чисел. Тому прийоми множення і ділення б/ц чисел вводяться по черзі, при цьому виділяють 3 етапи.1 етап. Множення і ділення на одноцифрове число;2 етап. Множення і ділення на двозначні, тризначні розрядні числа;3 етап. Множення і ділення на двоцифрове і трицифрове число.На кожному з етапі спочатку вивчають множення, а потім ділення. Поряд із множенням, ділення абстрактних чисел вивчають множення і ділення відповідних іменних чисел. Розглянемо спочатку перший етап множення. На підготовчому етапі повторюють:

1. Випадки множення з 1 і 0; 1•а = а; а • 1 = а; а • 0 = 0; 0 • а =0;

2. Розглядають множення розрядних чисел на одноцифрове 40 • 2; 400 • 2; 4000 • 2; 4 сот. • 2;

3. Множення двоцифрового числа на одноцифрове (на основі властивості множення суми на число).

13 • 4 = 40 + 12 = 52 , або (5+5+3)•4=52

2 етап - це множення на розрядні числа. Це множення на 10, 100, 1000, а потім 40, 400, 4000 тут використовують властивості множення числа на добуток. Наприклад: 14 • 60 = 14•(6 • 10) = 84 • 10 = 840. Після усного множення на розрядні числа вводять письмове множення на ці числа. Особливої уваги заслуговують приклади, у яких обидва множники закінчуються нулями. Наприклад: 20 • 30 = 600; 400•50 = 20000; 8000•70 = 560000

3 етап - це множення на 2 цифрове і трицифрове число. Роботу починають з усного множення. Наприклад: 16 • 12 = 16 • (10 + 2) = 160 + 32 = 192 (множення суми на число). Потім пропонують важчий випадок. Після розгляду загальних випадків множення на двоцифрове і трицифрове число вводяться окремо випадки: множення чисел, у записі яких на кінці і в середині є нулі. При множенні складених іменованих чисел йде заміна на прості іменовані числа і виконується дія, як над абстрактними числами, (натуральними)

31.Методика вивчення письмових прийомів множення багатоцифрових чисел на двоцифрове і трицифрове число. Множення на дво- і трицифрові числа Передумовою для успішного вивчення множення на двоцифрове число є вміння учнів виконувати письмове множення на одноцифрове число та розрядні числа. Теоретична основа множення на двоцифрове нерозрядне число — властивість множення числа на суму. Опрацювання матеріалу розпочинають з множення двоцифрового числа на двоцифрове. (На початку навчального року учні 4 класу вже розглядали цей випадок у межах 1 000). Учням пропонують прочитати пояснення про усний і письмовий способи знаходження добутку чисел 32 і 36. При письмовому множенні множники розміщують так, щоб одиниці були записані під одиницями. Множення розпочинають з одиниць. При множенні на десятки цифри другого неповного добутку починають записувати під десятками. Останньою дією знаходять суму неповних добутків. Учитель пропонує учням прочитати спочатку перший неповний добуток, а тоді другий неповний добуток (96 дес). Множення на трицифрове число з усіма розрядами не викликає труднощів. Для введення нового виду множення доцільно розглянути два схожих добутки, наприклад: 373 • 47 і 373 • 247. Спостереження показують, що в окремих учнів виникають труднощі при множенні чисел, які містять нулі. Для запобігання помилкам застосовують коментоване розв'язування. Подамо зразок коментування. Спочатку 3 054 множимо на 4 одиниці і в результаті отримуємо одиниці. Результат цього множення починаємо записувати під одиницями: 4 на 4, буде 16, пишемо 6, 1 запам'ятовуємо; 5 на 4, буде 20 і ще 1, буде 21, пишемо 1, а 2 запам'ятовуємо; 0 на 4, буде 0 і ще 2, пишемо 2; 3 на 4, буде 12, записуємо 12. У числі 204 — 0 десятків. Тому 3 054 будемо відразу множити на 2 сот. І в результаті отримаємо сотні. Результат цього множення починаємо * записувати під сотнями: 4 на 2, буде 8, цифру 8 записуємо на місці сотень; 5 на 2, буде 10, 0 пишемо, 1 запам'ятовуємо і т. д. Маємо два неповних добутки: перший неповний добуток — 12 216, другий неповний добуток — 6 108 сот. Добуток — 623 016.

32. Методика вивчення письмових прийомів ділення багатоцифрових чисел на двоцифрове і трицифрове число. Продовження формування навиків письмового ділення здійснюється в концентрі «Багатоцифрові числа», де діти вчаться ділити багатоцифрове число на одноцифрове та двоцифрове число і знайомляться з діленням на трицифрове число. Письмове ділення – це складна дія, яка передбачає виконання послідовних елементарних дій, які самі по собі теж складаються з певних операцій, а саме дій:визначення 1-го неповного діленого; визначення найвищого розряду частки; визначення кількості цифр в частці; виконання ділення з остачею під час ділення неповного діленого на дільник; визначення числа одиниць певного розряду, що розділилися; визначення числа одиниць певного розряду, що не розділилися; перевірки вірності відповідної цифри частки; утворення наступного неповного діленого. Зокрема в певних випадках письмового ділення застосовуються ще й прийом знаходження цифри частки на підставі заміни дільника меншим круглим числом і засіб перевірки пробних цифр частки. Ділення багатоцифрового числа на двоцифрове. Спочатку розглядають ділення трицифрового числа (без остачі і з остачею) на двоцифрове з одноцифровою часткою, звернувши увагу на спосіб знаходження цифри частки. Пояснення. Розгляньмо вираз на ділення трицифрового числа на двоцифрове з остачею. Ділене 752, дільник 86. Цифру частки будемо добирати, а потім випробовувати. Щоб легше було добирати, замінимо дільник меншим розрядним числом. Це буде 80. Поділимо 752 на 80; для цього достатньо 75 поділити на 8, буде 9. Перевіряємо усно число 9. 80 помножити на 9, буде 720 та ще 6 помножити на 9, буде 54, разом більше, ніж 752. Цифра 9 не підходить. Візьмемо число 8. 80 помножити на 8, буде 640 та ще 6 помножити на 8, буде 48, разом 688. 688 менше, ніж 752. Цифра 8 підходить. Запишемо її в частку. Знайдемо, скільки одиниць залишилося поділити. 752 відняти 688, буде 64. Частка 8, остача 64.

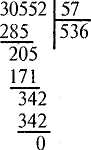
"Ділення багатоцифрового числа на двоцифрове (загальний випадок)". Перше неповне ділене 305 сот. Отже, вищим розрядом частки будуть сотні. У частці буде 3 цифри. Будемо шукати першу цифру частки. Поділимо 30 на 5, буде 6. Перевіряємо число 6 усно. 50 помножити на 6, буде 300 та ще 7 помножити на 6, разом буде більше, ніж 305. Отже, цифра 6 не підходить. Візьмемо число 5. Перевіримо його. 57 помножити на 5, буде 285. 285 менше, ніж 305, тому цифра 5 підходить. Запишемо її в частку. Віднімемо 285 від 305, буде 20. Аналогічно знаходимо другу і третю цифри частки. З учнями треба грунтовно опрацювати випадки ділення, коли частка містить нуль.

33. Загальні питання методики розв'язування задач у початковому курсі математики.Засобом переходу від операцій над множинами предметів до дій над натуральними числами є задачі. Математичну задачу розуміють як будь-яку вимогу обчислити, побудувати, довести що небудь, що стосується кількісних відношень і просторових форм, створених людським розумом на основі знань про навколишній світ. Розв'язуючи задачі, учні спираються на уявлення про предмети, що згадуються в умові, але оперують уже числами. Цей процес складається з таких етапів: ознайомлення зі змістом задачі; відшукання способу розв'язування; розв'язування задачі; перевірка розв'язання і відповідь. Розгляньмо методику роботи на кожному з цих етапів. Ознайомлення зі змістом задачі. Учень не повинен приступати до розв'язування задачі, не зрозумівши її. Учень ознайомлюється із задачею зі слів учителя або самостійно. Ступінь самостійності дітей залежить від рівня їхньої підготовленості і мети розв'язування задачі. При фронтальному ознайомленні вчитель читає або переказує задачу двічі. Першого разу читають з метою ознайомлення зі змістом загалом. Другого разу читають частинами і так, щоб кожна з них містила певну змістову "одиницю" тексту. Під час другого читання нових задач доцільно на дошці виконувати їх короткий запис. Читаючи задачу, вчитель паузами та інтонацією виділяє числові дані, слова, що визначають вибір дії, та запитання задачі. Щоб перевірити, як учні усвідомлюють умову задачі, вчитель задає їм запитання (за змістом окремих частин) або пропонує переказати всю задачу. Доцільним при ознайомленні та розв’язуванні задачі є використання наочності, вибір якої залежать від новизни і складності самої задачі. Аналіз задачі і відшукання способів її розв'язування. Пошук способу розв'язування здебільшого проводять у процесі розбору задачі від числових даних до запитання (синтетичний спосіб) або від запитання до числових даних (аналітичний спосіб). Спосіб розбору задачі від числових даних до запитання для дітей легший, але його застосування може давати зайві проби. Спосіб розбору задачі від запитання до числових даних більш цілеспрямований щодо складання лану розв'язування задачі, тут треба мати на увазі не одну яку-небудь дію, а хід міркування загалом. Однак для задач на три і більше дій він громіздкий. Задачі розв'язують усно або письмово: усно — це без запису арифметичних дій у зошит, письмово — із записом дій у зошитах. Перевірка розв'язання і відповіді. Перевірити розв'язання задачі — це з'ясувати, правильне воно чи ні. Для вчителя цей процес є засобом виявлення прогалин у знаннях учнів, а в поєднанні з аналізом та оцінюванням — засобом виховання інтересу до вивчення математики. Треба поступово виховувати в дітей почуття необхідності самоперевірки, ознайомлювати їх з найбільш доступними прийомами перевірки. З цією метою слід проводити бесіди, в яких буде проаналізовано допущені учнями помилки.

34. Прийоми формування навичок розв'язувати прості арифметичні задачі у першому класі чотирирічної початкової школи; їх типи, система розміщення у підручнику. Прості задачі - це задачі, які розв'язуються однією дією. Прості задачі в системі навчання математики відіграють дуже важливу роль. За допомогою розв'язування простих задач формують одне з центральних понять початкового курсу математики - поняття про арифметичні дії і ряд інших понять. Уміння розв'язувати прості задачі с підготовчим ступенем опанування учнями умінь розв'язувати складені задачі, бо розв'язання складеної задачі зводиться до розв'язування ряду простих задач. Розв'язуючи прості задачі, діти вперше ознайомлюються із задачею, її складовими частинами. У зв'язку з розв'язуванням простих задач діти опановують основні прийоми роботи над задачею. Тому вчитель повинен знати, як організувати роботу над простими задачами кожного виду. Порядок введення простих задач відповідає змісту програмного матеріалу. У 1 класі зокрема розглядаються такі типи задач: задачі на знаходження суми двох чисел, задачі на знаходження суми і остачі (Ці задачі вводяться після вивчення нумерації чисел першого десятка та ознайомлення з діями додавання і віднімання. Однак цьому передує пропедевтична робота — розв'язування задач без

застосування арифметичних дій, коли відповідь знаходять завдяки перелічуванню предметів або їхніх малюнків) задачі на збільшення і зменшення числа на кілька одиниць (пряма форма)( перш ніж розглядати задачі на збільшення або зменшення числа на кілька одиниць, учні порівнюють числа, збільшують і зменшують числа на 1 і 2. Вони усвідомлюють зв'язки: збільшити — означає додати, зменшити — означає відняти.), задачі на різницеве порівняння двох чисел (розглядають наприкінці вивчення першого десятка, а на кратне порівняння — під час вивчення табличного множення і ділення),задачі на знаходження невідомого доданка. Основними прийомами формування навичок розв’язування простих задач є: вправляння (тобто постійне розв’язування таких задач, в якості урочних та позаурочних завдань), розв’язування за аналогією ( при першому знайомстві вчитель звертає особливу увагу дітей на новий тип задачі, не називаючи його, детально розглядає алгоритм її розв’язування, і при наступному розв’язуванні проводить аналогію з попереднім).