Задача* 55.

Ознака зростання (спадання) функції

1. Тіло рухається прямолінійно за законом х(t)=-a₃t³ +2a₂t²+3a₁t+a₀, де t- час у секундах, a_0, a_1, a_2, a₃ - додатні сталі. Доведіть, що коли t змінюється в межах від 0 до 2a₂/3a₃, то швидкість руху тіла зростає.

2. Ядро вилітає з гармати вертикально вгору з початковою швидкістю, яка визначається за формулою v₀(t)=s/t+tgt/2, де s=2000 м, g=10 м/с². Через який час швидкість ядра почне зростати?

3. Рух тіла описується законом s(t)=15+2,5cos²t, де t- час у годинах. Доведіть, що дорога, якою рухається тіло, піднімається вгору.

4. Шлях руху туриста в горах визначається законом s(t)=12t+3sin3t, де t- час у годинах. Доведіть, що турист спускається з гори.

5. Диск кинуто вгору. Траєкторія його руху описується законом X(t)=t³/6+t²+8t. Чи зростатиме швидкість польоту диска через 3 хв після початку руху?

6. Джерело струму з електрорушійною силою Е і внутрішнім опором г підключено до реостата. За яких значень опору R реостата в зовнішній ланці теплова потужність зростає?

7. Рух катера по річці протягом 2 год описується законом s(t)=4,5t⁵-8t⁴+3t²-t. В який проміжок часу швидкість катера зростала?

8. З круглої колоди, діаметр якої дорівнює d, витесують брус з прямокутним поперечним перерізом, довжина основи якого дорівнює l, висота h. В яких межах може змінюватися довжина основи перерізу, щоб міцність бруса зростала (міцність бруса пропорційна добутку lh²)?

9. Швидкість човна v_ч відносно берега менша від швид­кості течії річки v. На цьому човні треба переправитись на проти­лежний берег річки. В яких межах може змінюватися кут напряму швидкості човна відносно течії, щоб знесення його течією не зро­стало?

10. У вертикальній трубі міститься рідина, яка досягає ви­соти Н. На деякій відстані h від основи треба пробити отвір у стінці труби, через який витікатиме рідина. В яких межах може змінюватися h, щоб дальність польоту цівки рідини збільшувалася?

11. Розчинність деякої солі у воді (1 л) виражається законом f(x)= 1/x+2/x²-4x³, де x - маса солі в грамах. Яка маса солі повністю розчиниться в 1 л води?

Критичні точки функції, максимуми і мінімуми

12. За якого значення а сума квадратів коренів рівняння х²+(2-а)х-а-3=0 буде найменшою?

13. Над центром круглого стола, радіус якого R, підвішено електричну лампу. Якою має бути відстань від лампи до стола, щоб освітленість на його краях була найбільшою?

14. Рятівник, що перебуває поблизу берега озера, повинен надати допомогу людині, яка тоне. Знаючи свою швидкість руху по суші v і по воді и, він має обрати траєкторію, за якої допомога надійде через мінімальний час. Якій умові має відповідати траєкторія?

15. Людина може рухатися по полю зі швидкістю v, а по шосе - зі швидкістю и. Їй потрібно з точки А на полі потрапити в точку С на шосе. Під яким кутом до шосе їй треба рухатися, щоб потрапити в точку С найшвидше?

16. При дії на механічну коливальну систему гармонічно змінюваної зовнішньої сили F= F₀sinωt в ній встановлюються ви­мушені коливання з амплітудою A=F₀ / m 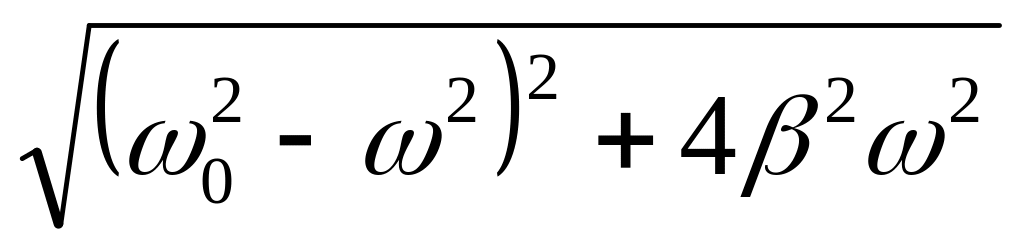, де т - маса системи, ω₀ - власна циклічна частота коливань системи, β - показник затухання, який характеризує силу опору середовища. За якого значення частоти ω періодичної зовнішньої сили настане резонанс, тобто амплітуда стане максимальною?

Приклади застосування похідної до дослідження функцій

17. Зобразіть траєкторію руху матеріальної точки, якщо рух її можна описати законом у=(х-1)(x+2)(х-3).

18. Температура t кипіння води і атмосферний тиск р пов'язані функціональною залежністю t(р)=р³-3р. За до­помогою графіка залежності t від p визначте значення тиску при t = 0°С.

19. Швидкість матеріальної точки задано рівнянням v(t)=t⁴/4-2t². Побудуйте графік залежності прискорення точки від часу t. Знайдіть прискорення точки в момент часу t=2.

20. Катер рухається за законом s(t)=-4t-t³/3+5t²/2, де t- час руху. Користуючись графіком швидкості руху катера, визначте, в який момент часу швидкість буде найбільшою.

21. Траєкторію руху човна по річці можна описати таким рівнянням: y= x⁴/4-4x³/3+2x². За допомогою графіка руху встановіть, чи торкнеться човен берега (осі ОХ).

22. Дротина після нагрівання набула форми, яку можна задати рівнянням y= 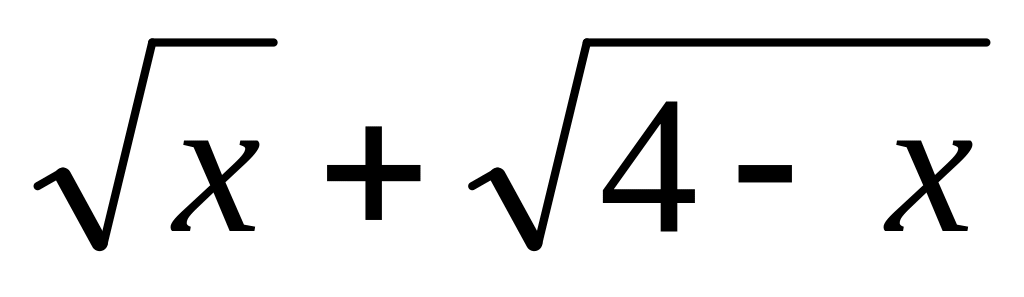. Зобразіть, якої форми набула дротина.

23. Поверхня рідини в пробірці має форму, яку можна опи­сати рівнянням y= 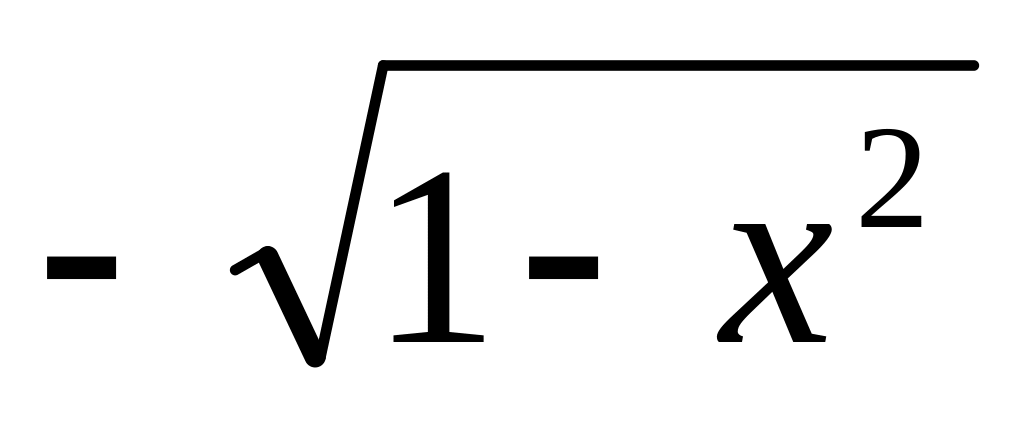. Зобразіть вигляд цієї поверхні.

Найбільше і найменше значення функції

24. З квадратного листа жерсті зі стороною а треба виготовити відкриту зверху коробку, вирізавши по кутах квадрати і згорнувши утворені краї. Якою має бути сторона основи коробки, щоб її об'єм був максимальним?

25. Бачок з квадратним дном має вміщувати 5 л рідини. За яких мінімальних розмірів бачка його поверхня без кришки буде найменшою (товщиною стінок знехтувати)?

26. Бачок з квадратним дном має вміщувати 10 л рідини. За яких мінімальних розмірів бачка його поверхня без кришки буде найменшою (товщиною стінок знехтувати)?

27. Під час роботи судна витрати N на 1 км шляху визна­чаються за формулою N=a/v+bv², де а і b - деякі коефіцієнти. Знайдіть найоптимальнішу швидкість судна за цих значень а і b.

28. Два велосипедисти почали рухатися одночасно у двох взаємно перпендикулярних напрямах до перехрестя, перебуваючи на відстанях 2 км і 3 км від нього. Швидкості велосипедистів відповідно дорівнюють 10 км/год і 12 км/год. Через який час відстань між ними буде найменшою, якщо рух триватиме 1 год?

29. Визначте лінійні розміри відкритого басейну місткістю V= 32 м³ з квадратним дном, щоб на облицювання його стін і дна було витрачено найменшу кількість матеріалу.

30. Сума двох діагоналей паралелограма дорівнює 2а, кут між ними 30°. Якими мають бути довжини діагоналей, щоб площа паралелограма була найбільшою?