Министерство образования Российской федерации

Государственное образовательное учреждение

высшего профессионального образования "Ивановская государственная архитектурно-строительная академия"

Кафедра высшей и прикладной математики

ПРОСТЕЙШИЕ КОНСТРУКЦИИ ПРИ ПРОГРАММИРОВАНИИ В СРЕДЕ ТУРБО-ПАСКАЛЬ

Методические указания и контрольные задания по информатике для студентов заочного отделения

№720

Иваново 2003

Составители: Волкова Н.В., Слизнева Т.Е. УДК 681.3 (076)

Простейшие конструкции при программировании в среде Турбо-Паскаль: Методические указания и контрольные задания по информатике для студентов заочного отделения / Иван. гос. архит. - строит, акад.; Сост.: Н. В. Волкова, Т. Е. Слизнева. - Иваново, 2003. - 32 с.

Методические указания содержат информацию для выполнения контрольной работы №1, которая состоит из 6 задач. Каждое задание содержит 10 вариантов. Номер варианта соответствует последней цифре зачетной книжки.

В каждом разделе приводятся в общем виде операторы, используемые при программировании, рассматриваются примеры составления программ, даются рекомендации, необходимые для выполнения работы, задаются контрольные вопросы.

Методические указания предназначены для студентов всех специальностей заочного отделения.

Рецензенты: кандидат технических наук,

доцент кафедры СМ ИГ АС А А.А.Краснов,

заведующая сектором ООР ЦНИТЛ.Ю.Петрова

ОГЛАВЛЕНИЕ

1. АЛГОРИТМЫ ЛИНЕЙНОЙ СТРУКТУРЫ.

ВЫЧИСЛЕНИЕ АРИФМЕТИЧЕСКИХ ВЫРАЖЕНИЙ 4

2. ПРОГРАММИРОВАНИЕ АЛГОРИТМОВ РАЗВЕТВЛЯЮЩЕЙСЯ СТРУКТУРЫ

3. ПРОГРАММИРОВАНИЕ АЛГОРИТМОВ ЦИКЛИЧЕСКОЙ СТРУКТУРЫ 18

1. Вычисление суммы и произведения 19

2. Программирование алгоритмов со структурой

вложенных циклов 20

3.3. Итерационные циклы 22

1. Табулирование функции 22

2. Вычисление суммы членов бесконечного ряда

с заданной точностью 25

БИБЛИОГРАФИЧЕСКИЙ СПИСОК................................31

2

1. Алгоритмы линейной структуры. Вычисление арифметических выражений

Алгоритм линейной структуры - такой алгоритм, в котором все предписания выполняются друг за другом в естественном порядке следования.

При описании таких алгоритмов в ТУРБО-ПАСКАЛЕ могут быть использованы следующие операторы:

1) Оператор присваивания

а: = V;

где а - переменная;

v - переменная, константа или выражение.

Например, если записано х:=0,5; у:=х * х - 6 * sin (х): то это значит, что переменной х присваивается значение константы 0,5, а переменной у -значение выражения х2 -б sin х (в данном случае при х = 0,5; у = -2,89).

Допустима также запись z: = z + х; которая называется рекурентной формулой, и читается как "новое значение переменной z становится равным старому значению переменной z плюс значение переменной х".

2) Операторы ввода и вывода данных

Write (< список вывода >);

Writeln (< список вывода >);

Read (< список ввода >);

Readln (< список ввода >);

<Список вывода> может содержать идентификаторы (имена переменных или констант) или текстовые константы (один или несколько символов, заключенных в апострофы), разделенные запятыми, а также форматы.

Например, оператор

3

Writeln ('Полученное значение y=, y:8:2);

выведет полученное значение у = -2,89 с новой строчки, а оператор Write с тем же списком вывода осуществит аналогичный вывод с текущей позиции (без перевода каретки).

Оператор Writeln; с пустым списком вывода обеспечит пропуск пустой строки и перевод каретки.

< Список ввода > состоит из одного или нескольких идентификаторов, разделенных запятыми.

Если в программе стоит оператор Readln (x, у); то во время выполнения программы происходит приостановление и компьютер будет ожидать ввода двух чисел, разделенных пробелом, т.е. надо набрать

0.5_2.3<Enter>.

Оператор Readln, с пустым <списком ввода> вызовет останов программы до нажатия какой-либо клавиши.

3) Составной оператор

В некоторых случаях (мы рассмотрим их позднее) полезно несколько операторов объединять вместе и рассматривать их как один оператор. Такая последовательность операторов заключается в begin-end (операторные скобки) и называется составным оператором.

Например,

Begin

x:=0,5

y:=x * x - 6 * sin(x)

End;

Рассмотрим алгоритм линейной структуры на конкретном примере.

4

Пример 1.1

Вычислить y= ² – .

где i = 55; K - любое целое, x - любое число, вводимое с клавиатуры (заметим, однако, что если вы попытаетесь ввести x < = O, то получите сообщение об ошибке. Почему?)

Прежде всего заметим, что в выражении дважды встречается одна и та

же константа 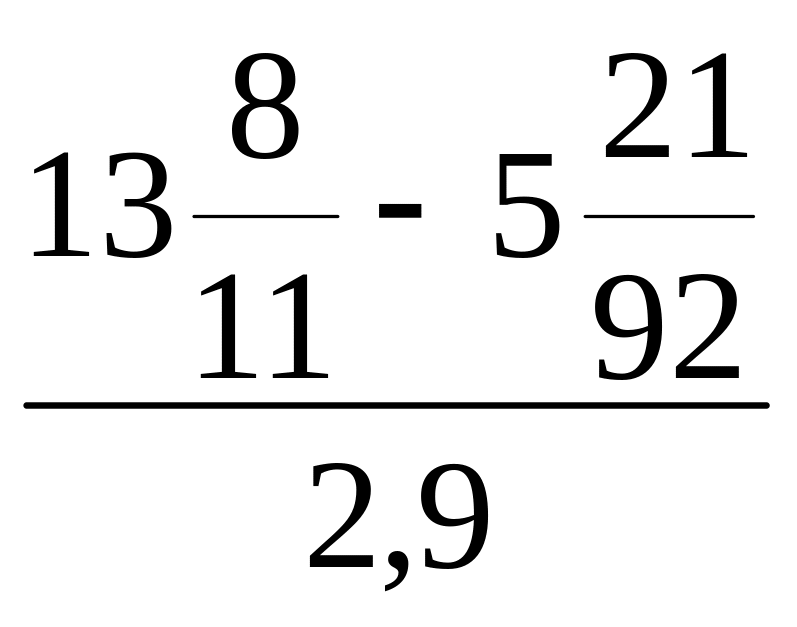. Обозначим ее C ₁ и перепишем исходное

выражение

Y=

Далее, в Турбо-Паскале нет функции tgx и отсутствует операция возведение в степень, поэтому tgC1, представим как

- как

ProgramFl;

{Раздел описания констант}

Const Cl=(13+8/ll-(5+21/92))/2.9; ,I=55

K: Integer=28; { Типизированная константа }

{ Раздел описания переменных }

Var x, у : Real;

{ Тело программы - обязательная часть }

5

Begin

Writeln ('Введите x > O);

Readln (x);

y:=K/(i * sin(Cl)/cos(Cl)) * sqr(x);

y:=y-exp(l/3 * LN(Cl))/(LN(x) + 2);

Writeln (‘x = __’, x, ‘K = __’, K, ‘y= _’, у);

End.

После того, как вы набрали текст программы и выполнили ее, вставьте следующие операторы:

1) сразу после Begin Writeln(‘Cl=_’,Cl);

и убедитесь, что константа C1 уже вычислена и имеет значение

2) перед End

K: = 7;

K: = 7.58;

I: = 7.58;

I: = 7;

Какие из этих четырех операторов будут выполняться, а какие нет? Почему?

Задания к теме № 1

B заданиях "а" выделить постоянную часть и вычислить ее в константном выражении до выполнения программы; вычислить значение выражения при всех конкретно заданных значениях переменных (если для какой-либо переменной заданы два значения, то это значит, что программа должна выполниться дважды, сначала с одним значением, затем с другим; каждое из них должно вводиться с клавиатуры).

B заданиях "б" ввести дополнительную переменную для промежуточных вычислений.

6

Например, в выражении y = arcsin3x + arcsin ³3x удобно вычислить сначала z = arctg , а затем y = z +z³.

Задачи 1-10

1) а) z = j·ln +2cos ,

где j = 3; j = 1/3; x – любое число;

б) p = tg + , x=0,2.

2) а) K= , где x=2,7; x=18; y-любое число;

б) С =

3) а) С = ,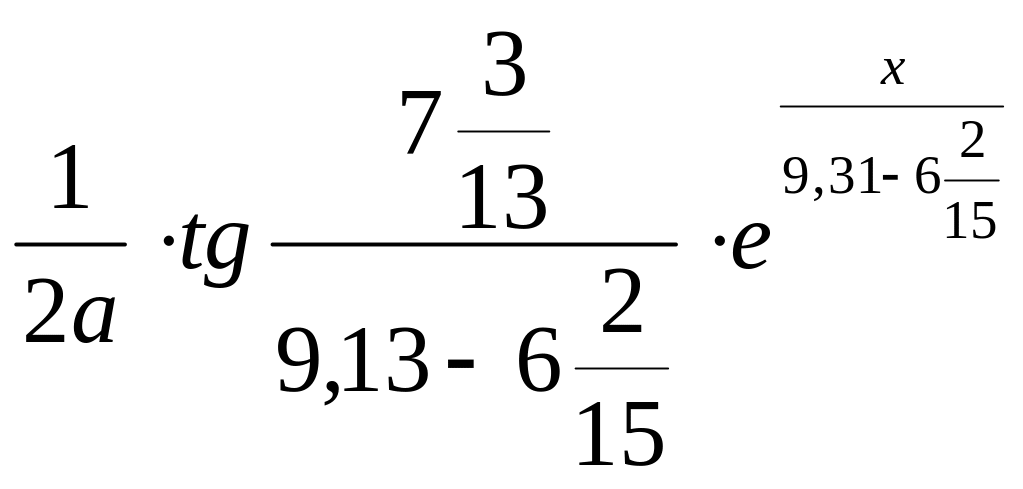

где a – любое число (а 0), x=3.51; x=6.9;

б) = 0,58e^1/x – tg arcsin2x

4) а) y = ,

где K- любое целое; С = 5,9; С = 1,2; x = -8;

б) u = 3x arcos lnx.

7

5. а) y = ,

где x=7; x=11; a – любое число;

б) d = .

6) а) z = ,

где К = 6.983 , x –любое число;

б) b = arcsin³ arcos ln x^.

7) а) q =arctg

где x=0,7; x=92,8; a-любое число;

б) W = tg .

8) а) y = ,

где z – любое целое (z 0); x=5,38; x=1,09;

б) z = .

8

9) a) z = ,

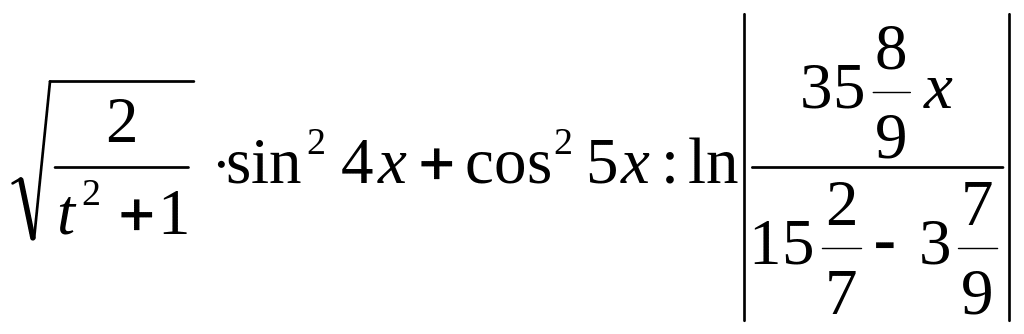где t – любое целое; x=2,34; x=5,12;

б) q = .

10. а) y = ,

где а=9; x=0,92; x=5,04;

б) P = .