1. Первая аксиома определяет уравновешенную систему сил. Система сил, приложенная к материальной точке, является уравновешенной, если под ее воздействием точка находится в со­стоянии относительного покоя или движется равномерно и пря­молинейно.

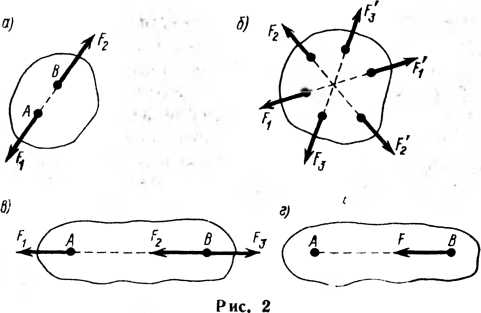
Вторая аксиома устанавливает условие равновесия двух сил. Две равные по модулю или численному значению силы (F_x — F₂),

1. 

приложенные к абсолютно твердому телу и направленные по одной прямой в противоположные стороны, взаимно уравновешиваются (рис. 2, а).

Третья аксиома служит основой для преобразования сил. Не нарушая механического состояния абсолютно твердого тела, к нему можно приложить или отбросить от него уравновешенную систему сил.

Четвертая аксиома определяет правило сложения двух сил. Равнодействующая двух сил, приложенных к одной точке, прило­жена в этой точке и является диагональю параллелограмма, построенного на данных силах.

1. Абсолютно твердые тела могут вступать во взаимодействие, в результате которого изменяется характер их движения. Сила является мерой этого взаимодействия. Например, взаимодействие планет и Солнца определяется силами тяготения. Действие силы на тело определяется тремя факторами: численным значением, направлением и точкой приложения, т. е. сила является векторной величиной.

Вектор силы изображается отрезком, на конце которого ста­вится стрелка. Стрелка указывает направление вектора, длина отрезка — значение вектора, измеренное в выбранном масштабе.

Вектор в тексте обозначают одной буквой со стрелкой наверху F,

а, V, а на схемах (рис. 1, а, б) стрелки не ставятся, так как само обозначение вектора в виде направленного отрезка достаточно наглядно характеризует его свойства.

Модуль или численное значение силы в СИ измеряется в ньюто­нах (Н). Применяют также и более крупные единицы измерения: 1 кильньютон (1 кН = 10^s Н), 1 меганьютон (1 МН = 10⁶ Н).

Системой сил называют совокупность нескольких сил, прило­женных к телу, точке или системе тел и точек.

Система сил, линии действия которых лежат в разных пло­скостях, называется пространственной. Если же линии действия рассматриваемых сил лежат в одной плоскости, система назы­вается плоской. Система сил с пересекающимися в одной точке линиями действия называется сходящейся. Сходящаяся система сил может быть как пространственной, так и плоской. Наконец, различают еще систему параллельных сил, которая аналогично сходящейся может быть пространственной или плоской.

Две системы сил эквивалентны, если взятые порознь они ока­зывают одинаковое механическое действие на тело. Из этого

определения следует, что две системы сил, эквивалентные третьей, эквивалентны между собой. Любую сложную си­стему сил всегда можно за- менить более простой эквивалентной ей системой сил. Одну силу, эквивалентную данной системе сил, называют равнодей­ствующей этой системы. Силу, равную по модулю равнодей­ствующей и направленную по той же линии действия, но в проти­воположную сторону, называют уравновешивающей силой. Если к системе сил добавлена уравновешивающая сила, то полученная новая система находится в равновесии и соответственно эквива­лентна нулю.

3. Связи и их реакции

Рассматриваемые в механике тела могут быть свободными и несвободными. Свободным называют тело, которое не испытывает никаких препятствий для перемещения в пространстве в любом направлении. Если же тело связано с другими телами, которые ограничивают его движение в одном или нескольких направле­ниях, то оно является несвободным. Тела, которые ограничивают движение рассматриваемого тела, называют связями.

При взаимодействии между телом и его связями возникают силы, противодействующие возможным движениям тела. Эти силы действуют на тело со стороны связей и называются реак­циями связей.

Реакция связи всегда противоположна тому направлению, по которому связь препятствует движению тела. Существование реакций обосновывается аксиомой о действии и противодействии. Для определения реакций связей используют принцип освобож­дения от связей. Не изменяя равновесия тела, каждую связь можно отбросить, заменив ее реакцией.

1.2. Плоская система сходящихся сил

Силы называют сходящимися, если их линии действия пересе­каются в одной точке. Различают плоскую систему сходящихся сил, когда линии действия всех данных сил лежат в одной пло­скости, и пространственную систему сходящихся сил, когда линии действия сил лежат в разных плоскостях.

Рассматриваемая система сходящихся сил находится в равно­весии, когда алгебраические суммы проекций ее слагаемых на каж­дую из двух координатных осей равны нулю.

Зависимости (12) называют уравнениями равновесия плоской , системы сходящихся сил и используют при аналитическом ре­

шении задач. В дальнейшем для упрощения записи уравнений равновесия будем опускать индексы у сумм.

1.3. ПАРА СИЛ И МОМЕНТЫ СИЛ.

5.Две равные и параллельные силы, направленные в противопо­ложные стороны и не лежащие на одной прямой, называются парой сил.

6. Действие пары сил на твердое тело, как показывает опыт, состоит в том, что она стремится вращать это тело. Способность пары сил производить вращение определяется моментом пары, равным произведению силы на кратчайшее расстояние (взятое по перпендикуляру к силам) между линиями действия сил. Обо­значим момент пары М, а кратчайшее расстояние между силами а, тогда абсолютное значение момента (рис. 19, а)

М - Fa = Га.

Кратчайшее расстояние между линиями действия сил назы­вается плечом пары, поэтому можно сказать, что момент пары сил по абсолютному значению равен произведению одной из сил на ее плечо.

7. Момент силы относительно точки и оси

Момент силы относительно точки определяется произведением модуля силы на длину перпендикуляра, опущенного из точки на линию действия силы (рис. 23, а).

При закреплении тела в точке О сила F стремится поворачи­вать его вокруг этой точки. Точка О, относительно которой бе- рется момент, называется центром момента, а длина перпенди­куляра а — плечом силы относительно центра момента.

Момент силы F относительно О определяется произведением силы на плечо

М₀ (F) = Fa.

1.4

5.Опорные устройства балочных систем

Шарнирно-подвижная опора (рис. 36, а). Эта опора допу­скает поворот вокруг оси шарнира и линейное перемещение па­раллельно опорной плоскости. В этой опоре известны точка при­ложения опорной реакции — центр шарнира и ее направление — перпендикуляр к опорной плоскости. Здесь остается неизвестным

Шарнирно-неподвижная форма (рис. 36, в). Эта опора допу­скает поворот вокруг оси шарнира, но не допускает никаких линейных перемещений.

Жесткая заделка (защемление) (рис. 36, г). Такая опора не допускает ни линейных перемещений, ни поворота. Неизвест­ными в данном случае являются не только значение и направление реакции, но и точка ее приложения. Поэтому жесткую заделку

заменяют силой реакции R_A и парой сил с моментом М_А.

10. Поверйем силы Ft и F2 на произвольный угол а, т. е. изменим их направление, сохранив параллельность. При этом равнодей¬ствующая останется равной их сумме, параллельной им, направ¬ленной в ту же сторону, а линия ее действия опять поделит пря¬мую АВ на части, обратно пропорциональные значениям задан¬ных сил. На рис. 42, а точкой С обозначено пересечение линии

действия равнодействующей в линией АВ. Эта точка называется центром параллельных сил, и ее положение не зависит от направ¬ления слагаемых сил Любое тело можно рассматривать как состоящее из большого числа малых частиц, на которые действуют силы тяжести. Все эти силы направлены к центру Земли по радиусу. Так как раз¬меры тел, е которыми приходится иметь дело в технике, ничтожно малы по сравнению в радиусом Земли (значение его около 6371 км), то можно считать, что приложенные к частицам еилы тяжести параллельны и вертикальны. Следовательно, силы тяжести от¬дельных частиц тела образуют систему параллельных сил. Равно¬действующую этих сил называют силой тяжести.

Центр параллельных сил тяжести, действующих на все ча¬стицы тела, называется центром тяжести тела. Центр тяжести тела не меняет своего положения при повороте тела.