План практичного заняття

1. Основні концепції планування експерименту.

2. Повний факторний експеримент.

3. Дробовий факторний експеримент.

4. Методи оптимізації.

Термінологічний словник

Ітера́ція (рос. итерация, англ. iteration, нім. Iteration f, Iterierung f) – 1) повторне застосування математичної операції (зі зміненими даними) при розв’язанні обчислювальних задач, яке дає можливість поступово наблизитися до правильного результату.

2) результат багаторазового повторення якоїсь математичної операції.

Оптиміза́ція (рос. оптимизация, англ. optimisation, нім. Optimierung f) – процес надання будь-чому найвигідніших характерис­тик, співвідношень. Задача О. сформульована, якщо задані: критерій оптимальності (економічний – тощо; технологічні вимоги – вихід про­дукту, вміст домішок в ньому та ін.); параметри, що варіюються (напр., температура, тиск, величини вхідних потоків у процесах пере­робки гірничої та ін. сировини), зміна яких дозволяє впливати на ефективність процесу; математична модель процесу; обмеження, пов’язані з економічними та конструктивними умовами, можливос­тями апаратури, вимогами вибухобезпеки та ін.

Рандомізація (рос. рандомизация, англ. randomization, hashing, нім. Randomisation f) – розташування об’єктів у випадковому порядку. Застосовується, наприклад, для вибору порядку слідування окремих дослідів при плануванні експериментів тощо. Рандомізація дозволяє нівелювати систематичні (наприклад, періодичні) впливи факторів, що не контролюються.

Практичні завдання та методичні рекомендації до їх виконання

Практичне заняття 1

Завдання 1. Скласти матрицю повного факторного експерименту (ПФЕ) 2².

Виконуючи завдання, необхідно базуватися на попередніх знаннях про досліджуваний процес і згадати, що побудова матриці почина­ється з визначення нульового рівня факторів варіювання. За нульові рівні обирають, як правило, значення, які наближаються до оптимуму. Далі задаються значеннями інтервалів варіювання (враховують досвід попередніх дослідників за інформаційними джерелами).

Значення рівнів факторів варіювання надати у вигляді табл. 3.1.

Таблиця 3.1 – Рівні факторів варіювання

Рівень фактора	Фактор варіювання			Кодоване значення
	Х1–	Х2–
Нульовий рівень			0
Інтервал варіювання			і
Нижній рівень			–
Верхній рівень			+

Виконати робочі записи у зошиті й обґрунтувати обрані значення.

Далі скласти матрицю ПФЕ 2² у натуральних величинах та кодах і надати у вигляді табл. 3.2.

Таблиця 3.2 – Матриця повного факторного експерименту 2²

Дослід	Рівень фактора
	кодована величина		натуральна величина
	Х1	Х2	Х1	Х2
1
2
3
4

Надати пояснення до прийнятих рішень у табл. 3.2.

Завдання 2. У табл. 3.3 подано матрицю повного трифакторного експерименту. За допомогою цієї матриці побудувати дві можливі пів репліки 2^n–1.

Таблиця 3.3 – Матриця планування для повного факторного експерименту

Номер спроби				y
1	–1	–1	+1	y1
2	+1	–1	–1	y2
3	–1	+1	–1	y3
4	+1	+1	+1	y4
5	–1	–1	–1	y5
6	+1	–1	+1	y6
7	–1	+1	+1	y7
8	+1	+1	–1	y8

При виконанні завдання повторити, що дробовий факторний експеримент (план) – експеримент, в якому реалізується лише части­на числа можливих поєднань рівнів факторів, тобто

Практичне заняття 2

Завдання 1. Для перевірки точності та репродуктивності обраного методу реалізувати в експерименті нульовий рівень матриці. Перед­бачити кількість повторюваностей «n» у серії дослідів не менше 10. Таким чином, отримують «n» значень (табл. 3.4).

Таблиця 3.4 – Математична обробка результатів експериментів

№ з/п	Уk
1	У1 =
2	У2 =
…	Уп =
10	У10 =

Отримані експериментальні дані підлягають математичній обробці в такій послідовності:

1. Знаходять середнє арифметичне значення критерію оптимізації «У» за формулою:

де У_k – значення параметра в окремих серіях паралельних дослідів;

k – номер повторності в серії дослідів;

n – кількість дослідів.

2. Визначають відхилення від середнього значення для кожного результату 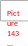і заносять до табл. 3.4.

Розраховані відхилення характеризують абсолютну помилку виз­начення. Досліди виконано найточніше, коли помилка має найменше значення.

3. Обчислюють експериментальну оцінку дисперсії репродуктив­ності для кожного результату У_k.

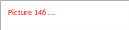
Дисперсія показує, як отримані результати групуються навколо середньоарифметичного значення. Таким чином, дисперсія характе­ризує ступінь розкиду У_k навкруги .

4. Розраховують експериментальну оцінку стандартного відхи­лення окремого визначення Така оцінка є середньоквадратич­ною помилкою окремого визначення:

5. Визначають середню дисперсію відтворювання середнього значення виходу процесу (параметр оптимізації):

Значення дисперсії репродуктивності необхідне для подаль­ших розрахунків.

6. Обчислюють експериментальну оцінку стандартного відхи­лення середнього результату, який характеризує репродуктивність методу дослідження:

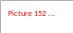
Зробити висновки.

Практичне заняття 3

Завдання 1. Отримані на попередньому занятті експериментальні дані перевірити за такими критеріями:

1. Надійність отриманих результатів перевіряють за допомогою критерію Стьюдента t_a.

Критерій t_a з довірчою ймовірністю а показує, у скільки разів модуль різниці між істинним значенням величини, яка визначається у_k, та середнім значенням більший за стандартне відхилення серед­нього результату

Значення t_a можна знайти за даними, поданими в дод. А. Критерій Стьюдента приймають залежно від обраної довірчої ймовірності а та кількості ступенів свободи f, що залежить від кількості дослідів n. Як правило, для хіміко-технологічних досліджень обирають Кількість ступенів свободи знаходимо за формулою:

де n – кількість дослідів.

Після визначення стандартного відхилення середнього результату і критерію t_a, розраховують помилку отриманого середнього результату _а:

2. Встановлюють інтервал, у якому з довірчою ймовірністю 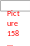знаходиться середній результат

3. Розраховують відносну помилку у відсотках:

4. Виключають грубі помилки. Якщо відносна помилка виявля­ється великою, тоді аналізують отримані результати на наявність гру­бих помилок і виявляють сумнівні результати. Розглядають критерій Стьюдента ( ) для сумнівного результату:

Якщо розрахункове значення критерію Стьюдента буде більше, ніж табличне ( ), результат вважається грубою помилкою та виклю­чається з подальших розрахунків. Потім повторюють обробку експе­риментальних даних.

Обґрунтувати прийняті рішення, зробити висновки і відобразити все у зошиті.

Завдання 2. Розробити рівняння регресії процесу, що вивчається, розрахувати коефіцієнти рівняння регресії та провести його аналіз. Процес обрати самостійно. Результати занести у зошит.

Для виконання завдання обрати процес, який пов’язаний з темою Вашого дослідження.

ЗРАЗОК А

Виконання завдання провести відповідно до алгоритму визначення математичної моделі:

1. Обрати форму математичної моделі.

2. Розрахувати коефіцієнти рівняння регресії.

3. Обчислити дисперсію репродуктивності.

4. Перевірити вагомість коефіцієнтів рівняння регресії.

5. Перевірити адекватність моделі.

Необхідно згадати, що математична модель процесу з будь-якою кількістю факторів варіювання (вхідні параметри процесу) можуть бути представлені у загальному вигляді рівнянням регресії:

де – коефіцієнти рівняння при відповідних факторах;

х – фактори рівняння;

у – вихід процесу.

Це рівняння служить математичною моделлю досліджуваного процесу.

Для двохфакторного експерименту модель має вигляд:

де b0 – залишковий член рівняння регресії;

– вектор виходу;

При визначенні коефіцієнтів рівняння регресії використовують кодовані значення змінних, які мають значення +1 та –1 відповідно до матриці експерименту. Формули для визначення лінійних коефіцієнтів рівняння регресії мають вигляд:

( ).

При обчисленні коефіцієнта регресії кожного фактора фактично треба скласти значення вектора виходу у всіх дослідах (тобто ), взятих зі знаками відповідного кодованого фактора в матриці плану­вання, і одержану суму поділити на загальне число дослідів.

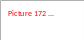
де m – число повторювань u-го досліду.

Практичне заняття 4

Завдання 1. Провести аналіз коефіцієнтів рівняння регресії за до­помогою перевірки вагомості коефіцієнтів регресії у такій послідов­ності:

1. Знайти дисперсію репродуктивності коефіцієнта :

де N – кількість дослідів (рядків матриці).

2. Визначити середньоквадратичну помилку визначення коефі­цієнтів регресії

3. Перевірити вагомість коефіцієнтів регресії. Той коефіцієнт вважається вагомим, якщо виконується для нього нерівність:

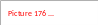
Якщо абсолютна величина коефіцієнта більша помилки його визна­чення, тоді цей фактор впливає на процес і вважається вагомим. Коли всі коефіцієнти рівняння регресії є вагомими, тоді оцінку його адекватності не проводять і вважають рівняння регресії адекватним реальному процесу. Невагомі фактори виключаються з рівняння і воно записується у новому вигляді.

У зошиті записати результати розрахунків і зробити висновки.

Завдання 2. Провести перевірку адекватності моделі реальному процесу. Необхідно згадати, що перевірка гіпотези про адекватність моделі реальному процесу відбувається за допомогою критерію Фіше­ра (F). Розрахунки провести у такій послідовності:

1. Розрахувати вихід процесу (у) для кожного варіанта досліду за кінцевим рівнянням регресії. Для цього в нове рівняння підставити кодовані значення факторів варіювання (+1) і (–1). Розрахунки оформити у вигляді табл. 3.5.

2. За кожним варіантом досліду знайти різницю між розрахунковим значенням виходу (у) та його експериментальним значенням (у_к) (того ж варіанта досліду).

Таблиця 3.5 – Розрахунки дисперсії адекватності рівняння регресії

Дослід	Рівень фактора
	Х1	Х2
1
2
3
4

3. Розрахувати дисперсію адекватності ( ):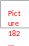

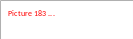
де N – кількість дослідів основного експерименту;

n – кількість вагомих коефіцієнтів у рівнянні регресії.

4. Знайти розрахункове значення критерію Фішера F_р:

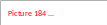
5. За таблицею (дод. Б) обрати значення критерію Фішера. Для цього враховують число ступенів свободи ( ).

6. Порівняти табличне значення критерію Фішера з його розра­хунковим.

При виконанні нерівності: рівняння вважається адекватним і може бути використане для розрахунку виходу процесу за будь-яких значень факторів між верхнім і нижнім рівнями.