13 Измерение тока Холла.

Режим измер. тока Холла (ТХ) имеет место при холловском поле E_z=0, т.е холловские грани образца закорочены. Теоретически это выпол-ся в бесконечном образце, (т.е. длина парал-да >>его линейного размера), а практически реализ-ся в диске Карбино(один электрод размещен в центре диска в виде оси, а второй- по ободу диска в виде кольца). А также в прямоугольном образце, ширина которого >> длины. Носители заряда под действием силы Лоренца откл-ся вдоль оси z и встреч. противод-вия поперечн. поля E_z и обр-т попер-й компонент тока j_z. В этом случ. угол Холла опред-ся

.

Векторы результ-го тока и результ-го поля E_z откл-ся в разные стороны относ-но оси х. Тогда составл-щая

j_z=μj_xB.

В режиме ТХ прим-ся м-ды измер. j_z в разрыве токов электрода, в дан. сл. измер-ные вел-ны U_x,I_x,I_z.пропорц-ны произвед. размеров a*b*j_z. Прод. и поперечн. токи = сумме токов, протек-щих вдоль токовых контактов и через них.

I_x=I_x1+I_x2, I_z=I_z1+I_z2

По изм. вел-нам м.б. определены только два основных параметра электрон. переноса: σ-уд. провод-сть и μ-подвижность.

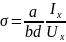
d- толщина образца

М-д ТХ позв-ет проводить измерение на более высокоомных материалах, чем м-д ЭДС Холла. Этому способствует такое соотношение геом. размеров образца, при кот. его сопротивление между токовыми контактами ниже, чем при измер. ЭДС Холла.

Небольшое различие в хар-ках половинок контактов практ-ки не влияет на рез-ты измерений, т. к. небольшая асимметрия расположения контактов при измерении ЭДС приводит к образованию значительной неэквипотенциальности, которая затрудняет измерение.

14 Измерение подвижности методом магнитосопротивления.Для определения концентрации и подвижности носителей заряда необходимо измерить проводимость образца и постоянную Холла. Измерения обычно проводят следующим образом: на верхней грани образца размещают два зонда 1 и 2 вдоль направления линий тока, а со стороны нижней грани устанавливают зонд 3, встречный одному из них. С помощью зондов 1 и 2 измеряют проводимость образца по двухзондовому методу, а зонды 1 и 3 служат для измерения холловской разности потенциалов.

E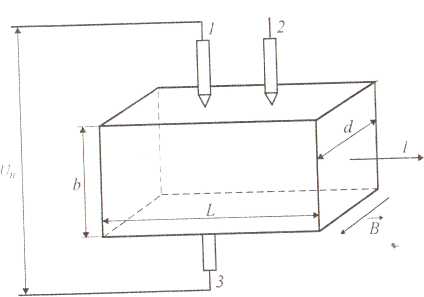 _z=U_н/b – холловское электрическое поле

j=I/S=I/bd – плотность тока

Холловская разность потенциалов:

U _н/b=R_н*I*B/bdU_н=R_н*IB/dR_н=U_н*d/IB

Метод магнитосопротивления: на исслед. образец наносятся омические контакты большой площади и через них протекают электрический ток I_x(вдоль оси х). В поперечном магнитном поле (вдоль оси z) в образце возникает холловский ток I_y. В данном случае холловский ток не компенсируется холловской разностью потенциалов, так как при геометрии образца, когда d/L<<1, токовые контакты закорачивают холловское поле.

Результирующий ток в образце будет направлен под некоторым углом к току I_х, что приведет к изменению сопротивления μ образца вдоль оси х.

μ_m=1/B* - магниторезистивная подвижность

где В – индукция магнитного поля; R(B) - изменение сопротивление образца, вызванное магнитным полем с индукцией В; R(0) – сопротивление образца.

Для того чтобы метод геом. магнитосопротивления обеспечивал высокую точность измерений, сопротивление контактов должно быть минимальным и пренебрежимо малы по сравнению с сопротивлением исследуемого образца.

15. Диэлектрические измерения – определение диэлектрических хар-тик материалов (диэлектрич. проницаемость, диэлектрич. потери). Помимо электротехнич. измерений могут применяться в аналитической химии в различных областях для определения содержания влаги, чистоты соединений. Явления, происходящие в помещенных в ЭП вещ-ве могут быть описаны с позиции двух теорий: электротехнической и молекулярной.Электротехническая теория. Идеальный конденсатор без потерь (вакуумный) хар-ся в цепях переменного тока сдвигом по фазе на 90° между током и напряжением. Такой конденсатор потребляет чисто реактивную мощность. Если конденсатор, имеющий вакуумную емкость С₀, заполнить каким-либо вещ-вом, то емкость возрастает в ε раз. Конденсатор представляет собой в общем случае две металлические пластины (обкладки), разделенные слоем диэлектрика и его емкость определяется соотношением С = εε₀S/d (ε = С/С₀), где εε₀ – абсолютная диэлектрическая проницаемость вещ-ва. Для практических приложений представляет интерес относительная диэлектрич.проницаемость. В реальных диэлектриках, помещенных в ЭП, имеют место активные потери энергии, а угол сдвига фаз между током и напряжением оказывается меньше 90°. Для хар-ки потерь используют понятие угла потерь θ, который равен 90° - ϕ, где ϕ – угол сдвига между током и напряжением для конденсатора с потерями. Согласно данной схеме tgθ = 1/2πfCR, f – частота переменного тока. Если емкость и активное сопротивление выразить через геометрические размеры конденсатора, то получим выражение tgθ = Sd/2πfεε₀Sρd = σ/2πfεε₀.Значение электропроводности и диэлектрич.проницаемости должны быть измерены при частоте f. В качестве эквивалентной схемы конденсатора с потерями выбирается схема конденсатора без потерь С₁ и сопротивления R₁, включенных последовательно. При этом угол потерь будет определяться по следующей формуле: tgθ = 2πfR₁C₁. Если измерения выполнены при фиксированной частоте, то обе эквивалентные схемы равноправны.При изучении поведения материалов в широком диапазоне частот требуется более сложная эквивалентная схема.Молекулярная теория. Различные вещ-ва в зависимости от их молекулярного строения можно разделить на две молекулярные группы: неполярные соединения (вещ-ва, у кот. при отсутствии внешнего ЭП центры + и – зарядов не совпадают) и полярные (центры + и – зарядов совпадают). При наличии внешнего ЭП в неполярных вещ-вах происходит деформационная поляризация или поляризация сдвига (смещение + и – зарядов, индуцирование дипольного момента), а в полярных вещ-вах – ориентационная поляризация (ориентирование диполей под действием ЭП). Результирующая молярная поляризация обусловлена деформ-ой и ориентац-ой поляр-ей. Эти процессы описываются комплексной диэлектрич.проницаемостью.ε* = ε’ – jε’’ = ε_∞ + (ε₀’ - ε_∞’)/(1 + jwτ), ε’ – активная составляющая диэлектрич.проницаемости; ε’’ – реактивная составляющая; ε_∞’ – при высоких частотах; ε₀’ – при низких f→0Гц; w – круговая частота; τ – время релаксации.Активная составляющая комплексной диэлектрич. проницаемости соответствует относит. диэлектрич. проницаемости, а реактивная составляющая хар-ет поглощение энергии в вещ-ве и называется коэф.диэлектрич.потерь. Составляющая комплексной диэлектрич.проницаемости и тангенс угла потерь связаны: tgθ = ε’’/ε’. Активная и реативная составляющие комплексной диэлектрич. проницаемости зависят от частоты (графики). Активная составляющая при постоянном токе или низких частотах сохраняет некоторое квазистатическое значение. При дальнейшем росте частоты, когда период ЭП становится соизмерим со временем релаксации, диэлектрич.проницаемость уменьшается. При дальнейшем росте частоты она приближается к новому постоянному значению (высокочастотной диэлектрич.проницаемости). В квазистатической области постоянные диполи успевают следовать за переменным полем. В области частот, где диэлектрич.проницаемость начинает уменьшаться с ростом частоты (начало области аномальных дисперсий) это синфазное следование диполей за ЭП нарушается. В области высоких частот ориентационная поляризация пропадает и остается лишь изменяющаяся под действием ЭП деформационная поляризация. Коэф.диэлектрич.потерь в области низких и высоких частот незначителен. Он резко возрастает в области аномальной дисперсии и достигает max в точке перегиба дисперсионной кривой. Время, в течение которого ориентационная поляризация уменьш-ся в ε раз после выключения поля, называется временем релаксации, т.е. это время является пост. времени затухания ориентационной поляризации. Если молекула имеет сложную форму (элипсоидальную), то для каждой из трех осей элипсоида есть свое время релаксации. Когда эти времена разнятся значительно-на дисперсионных кривых хорошо заметны 3 аномальных дисперсий. Если же значение времен релаксации близки, то дисперсионная область оказывается размытой.

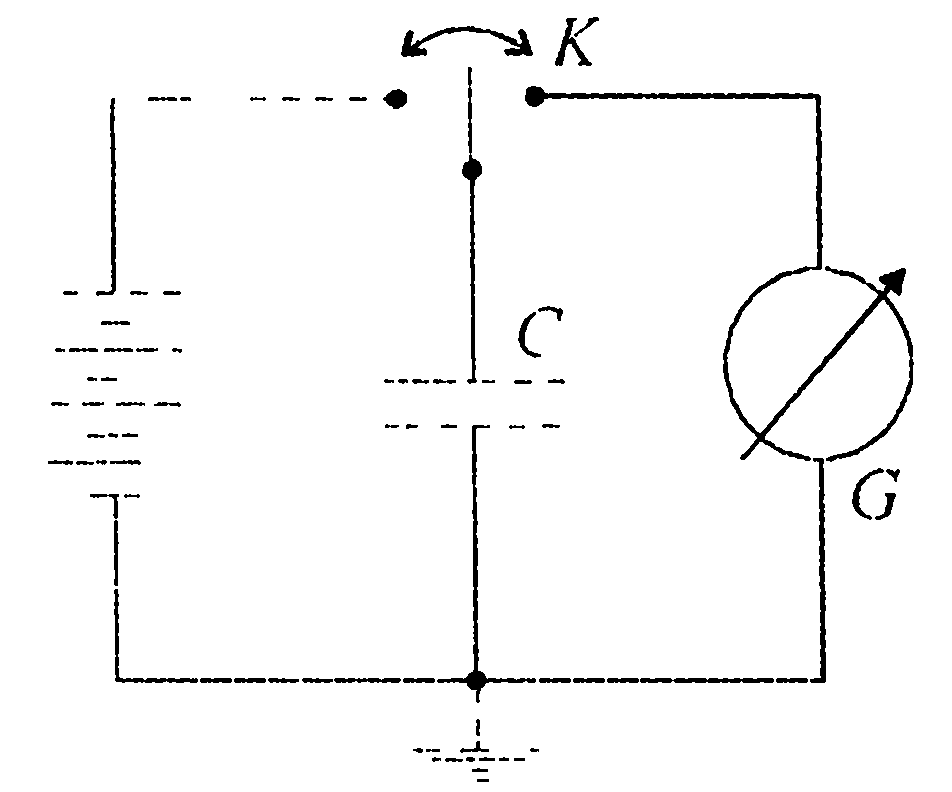
16. Измерение диэлектрической проницаемости методом баллистического гальванометра На практике измерение диэлектрич.хар-тик материалов либо проводят при фиксированной частоте достаточно низкой, чтобы измерения велись до области аномальных дисперсий, либо измеряют комплексную диэлектрич.проницаемость и тангенс угла диэлектрич.потерь – потерь в широком диапазоне частот. Измерение относит.диэлектрич.прониц. вещ-в обычно сводятся к расчету по измеренной емкости конденсатора с вещ-вом и известным геометрич.размером конденсатора. Величина статич.диэлектрич.проницаемости ε_0’ м.б. определена по емкости, измеренной методом баллистического гальванометра, кот.позволяет измерять диэлектрич.проницаемость на постоянном токе.

Данный метод основан на том, что исследуемая емкость заряжается до строго определенного напряжения и затем разряжается на баллистич.гальванометр. Отклонение указателя пропорционально кол-ву электричества, прошедшего через гальванометр. Емкость конденсатора вычисляют по известному заряду и напряжению на обкладках: С = Q/U. Метод обычно применяют для вещ-в с малой проводимостью.