4.4.2 Расчет верхнего пояса фермы

Расчет производим по максимальным расчетным сочетаниям усилий N_Sd = 709,17 кН, M_Sd = 117,37 кН · м, V_Sd=69,11кН (для стержней 2 и 7). Остальные элементы верхнего пояса из соображений унификации будут армироваться аналогично рассмотренным.

Усилия от длительно действующей нагрузки:

M_Sd,lt = кН · м,

N_Sd,lt= = кН.

Рабочая высота сечения верхнего пояса при c = с₁= 30 мм:

d = h – c = 250 – 30 =220 мм.

Эксцентриситет е_0N=

Расчёт в плоскости изгиба. Расчётная длина верхнего пояса фермы в плоскости изгиба при е₀=0,165м >(1/8)·0,3= 0,038 (табл.7.3 [1]) – l₀ = 0,8 · 2,986=2,39 м.

Радиус инерции сечения мм.

Так как l₀/i = 2390/ 72,17 = 33,12 > 34 – 12 · =34 – 12 ·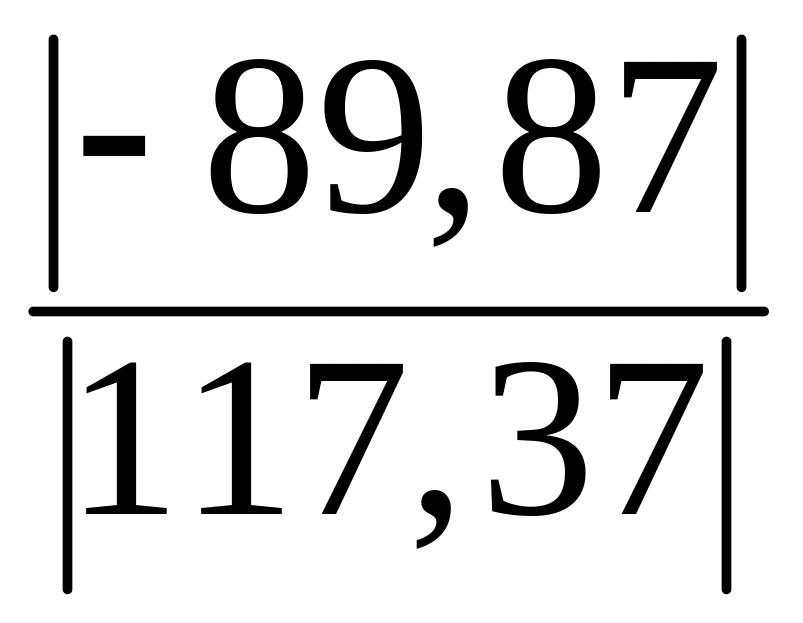 = 24,81 , то необходимо учесть влияние прогиба на эксцентриситет продольной силы.

где: M_min , М_max – больший и меньший изгибающий момент в пределах расчётной длины элемента, принимаются по таблице 6 для стержней 2 и 7.

При расчете элементов по прочности сечений, нормальных к продольной оси, на совместное действие изгибающих моментов и продольных усилий расчетный эксцентриситет определяется как

где: е_а-величина случайного эксцентриситета, принимается большая из велечин

мм; мм и 20мм.

Принимаем е_а=20мм. Тогда е₀=0,165+0,020=0,185м

где: I_c= м⁴;

здесь: кН·м;

кН·м;

- для тяжелого бетона;

- коэффициент, принимаемый равным , но не менее ;

- коэффициент, принимаемый для элементов без предварительного напряжения.

Коэффициент приведения

Момент инерции площади сечения арматуры относительно центра тяжести сечения элемента I_s при первоначально принятом коэффициенте продольного армирования ρ₁=0,025

м⁴

Коэффициент, учитывающий влияние прогиба на величину эксцентриситета:

Полный эксцентриситет с учетом влияния гибкости составляет

Расчётный изгибающий момент продольной силы относительно центра тяжести растянутой арматуры:

M_{Sd 1}= N_Sd · (e_tot + 0,5·h – c) = 709,17 · (0,218 +0,5 · 0,25 –0,03) =221,97кН· м.

Предполагая, что сечение находится в области деформирования 2 (k_s1=k_s2=1.0) определяем для симметричного армирования (т.к эпюра изгибающих моментов двухзначна в пределах элемента) величину относительной высоты сжатой зоны

Поскольку (таблица 2–2 приложения 2), то сечение находится в области деформирования 2. Расчет производится по случаю больших эксцентриситетов, используя алгоритм блок-схемы 2 приложения 6.

Требуемая площадь сжатой арматуры:

Минимальный процент армирования согласно табл. 11.1 [1] принимается равным , но не менее , принимаемого не менее 0,1% и не более 0,25%. .

Имеем: ;

К дальнейшим расчетам принимаем .

Минимальное количество сжатой арматуры исходя из принятого процента армирования

.

Принимаем армирование 3Ø28 S400 (Asc=1847мм²), что больше минимальной величины площади сечения.

С учетом принятой площади арматуры , при , коэффициент составит:

,

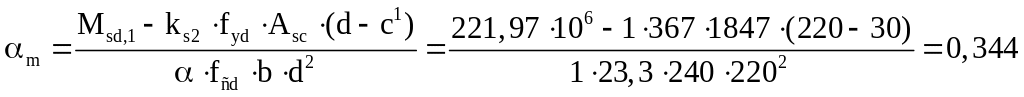По таблице 2–2 приложения 2 при .

По таблице 5–1 приложения 5 при и коэффициент

Тогда требуемое количество растянутой арматуры

Принимаем армирование 3Ø28 S400 (Ast=1847 мм²).

По результатам расчёта в сечениях стержней верхнего пояса безраскосной фермы устанавливаем:

– в растянутой зоне А_st = 3Ø28 S400 (Ast=1847 мм²).

– в сжатой зоне А_sc = 3Ø28 S400 (Ast=1847 мм²).

Расчёт из плоскости изгиба Расчётная длина панели верхнего пояса фермы из плоскости изгиба l₀ = 0,9·l = 0,9 · 3,010 = 2,709 м. Так как гибкость из плоскости изгиба

l₀ / b = 2,709 / 0,24 = 11,28 > l₀ / h =2,709 / 0,25 = 10,84 – гибкости в плоскости изгиба, то необходим расчёт прочности с учётом устойчивости из плоскости изгиба. Расчет производим как для центрально сжатого элемента (см. п. 2.4.2[2])