
- •Раздел 5
- •5. Поверхность задана уравнением , - точка на этой поверхности. Укажите уравнение касательной плоскости к данной поверхности в данной точке
- •21. Знакоположительный ряд будет сходящимся, если при сравнении со сходящимся знакоположительным рядом выполняется условие
- •Ряд сходится
- •Ряд расходится
- •37. Укажите определение смешанной производной второго порядка для функции
- •Раздел 6.
Раздел 5
1.
Укажите определение смешанной производной
второго порядка для функции
![]()
2.
Укажите определение частной производной
второго порядка по переменной y от
функции
![]()
3.
Поверхность задана уравнением
![]() ,
,
![]() - точка на этой поверхности. Укажите
уравнение касательной плоскости к
данной поверхности в данной точке
- точка на этой поверхности. Укажите
уравнение касательной плоскости к
данной поверхности в данной точке
4. Поверхность задана уравнением , - точка на этой поверхности. Укажите уравнение нормали к данной поверхности в данной точке
5. Поверхность задана уравнением , - точка на этой поверхности. Укажите уравнение касательной плоскости к данной поверхности в данной точке
6.
Функция двух
переменных (![]() и
и
![]() )
задана
неявно уравнением
)
задана
неявно уравнением
![]() .
Укажите формулу производной
.
Укажите формулу производной
![]()
7.
Функция
и
ее частные производные
![]() ,
,
![]() непрерывны
в точке
непрерывны
в точке
![]() .
Укажите необходимое условие существования
экстремума в этой точке
.
Укажите необходимое условие существования
экстремума в этой точке
1.
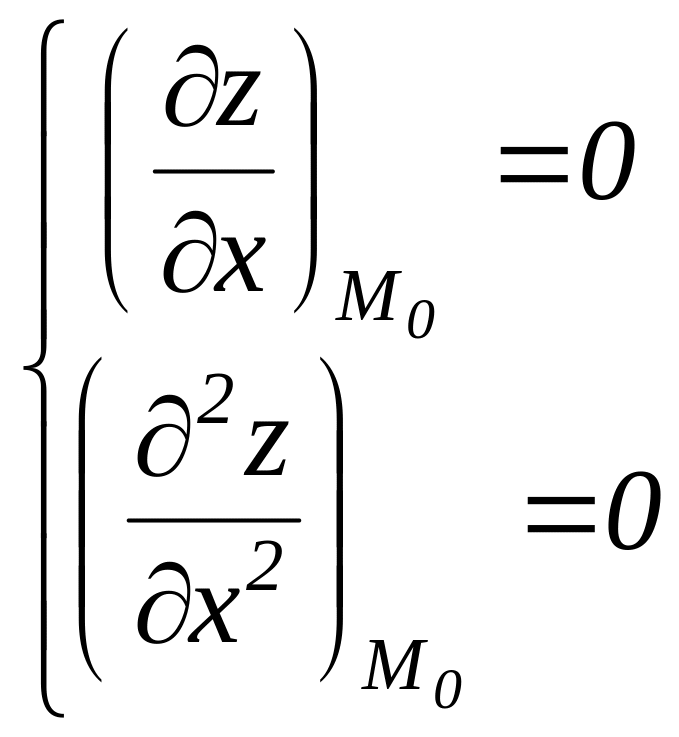 2.
2.
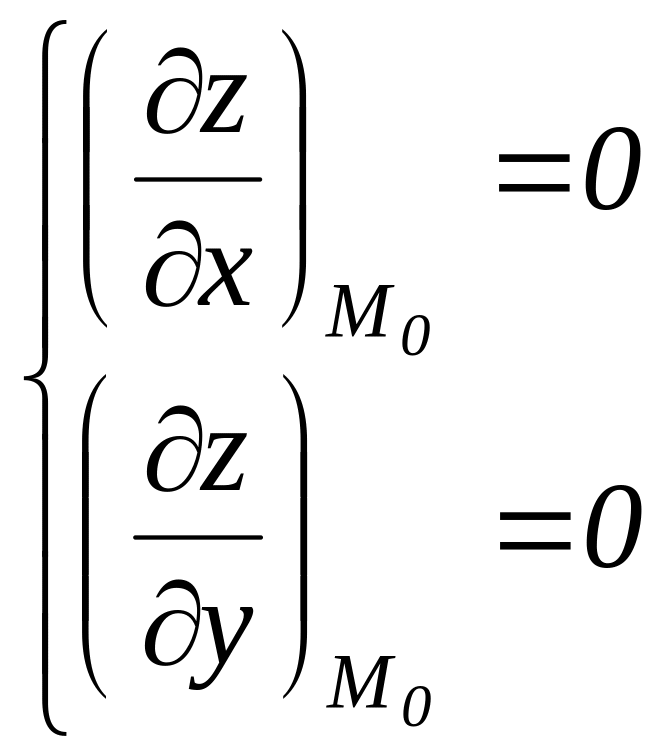 3.
3.
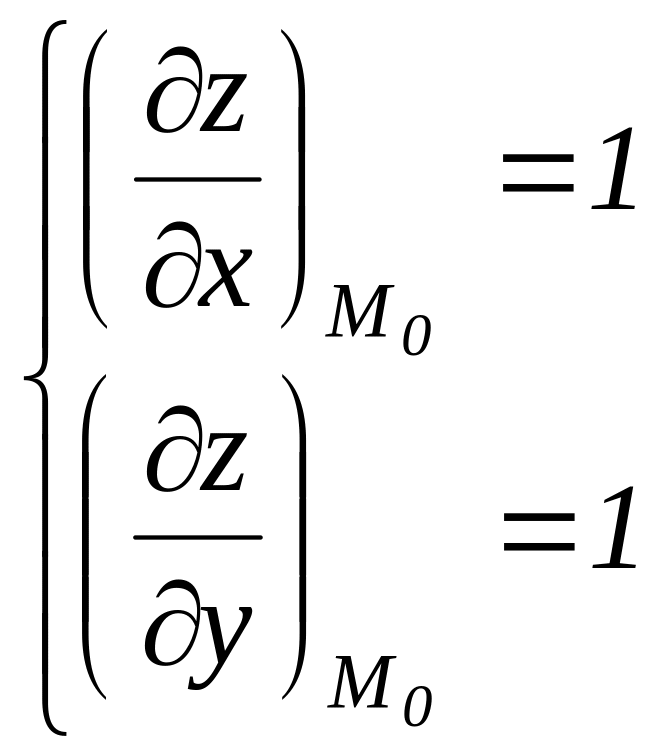 4.
4. 5.
5.
1
2
3
4
5
8.
Функция
![]() и
ее частные производные
и
ее частные производные
![]() ,
,
![]() непрерывны
в стационарной точке
непрерывны
в стационарной точке
![]() .
.
 ,
,
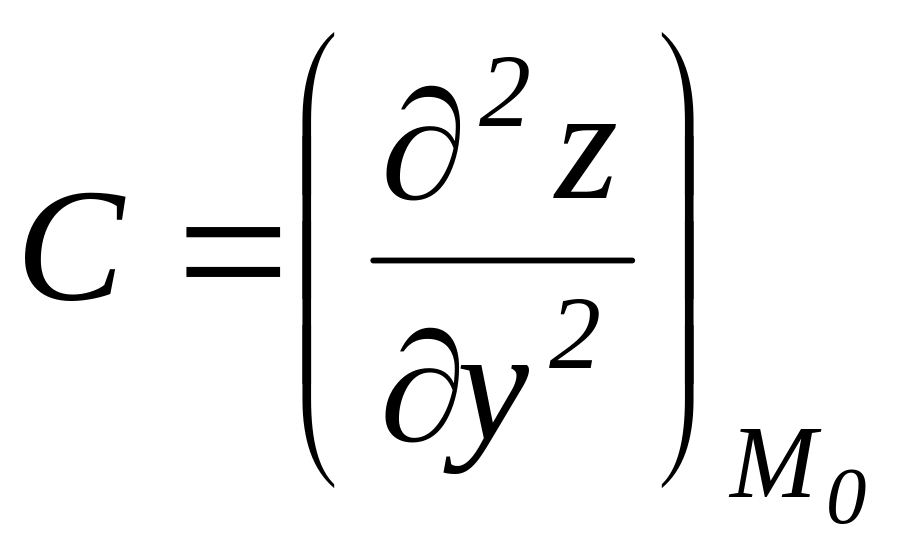 ,
,
![]() ,
,
![]() ,
,
![]() -
точка максимума, если:
-
точка максимума, если:
1.![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() 5.
5.![]()
1
2
3
4
5
9.
Функция
и
ее частные производные
,
![]() непрерывны
в стационарной точке
непрерывны
в стационарной точке
![]() .
.
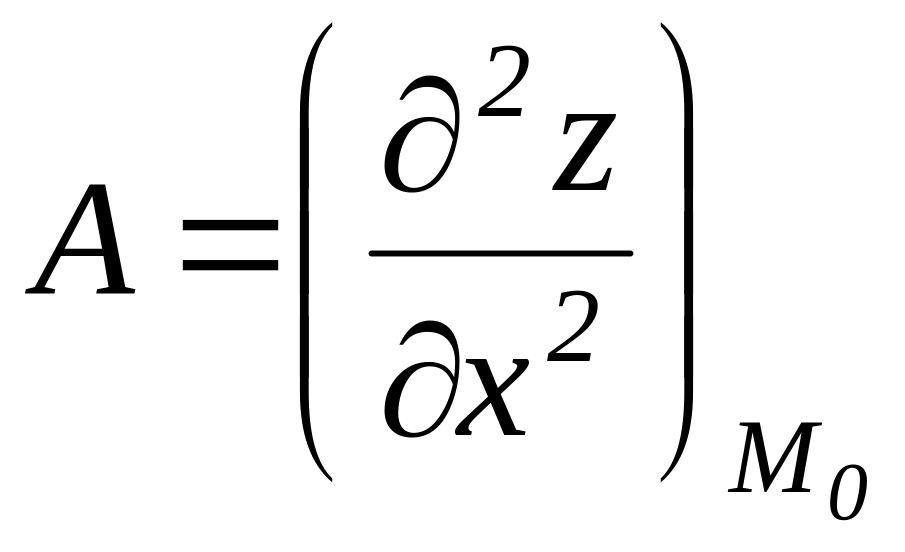 ,
,
,
,
,
,
![]() .
.
![]() -
точка минимума, если:
-
точка минимума, если:
1. 2. 3. 4. 5.
1
2
3
4
5
10.
Функция двух
переменных (
и
)
задана
неявно уравнением
![]() .
Укажите формулу производной
.
Укажите формулу производной
![]()
11. Ряд называется сходящимся, если
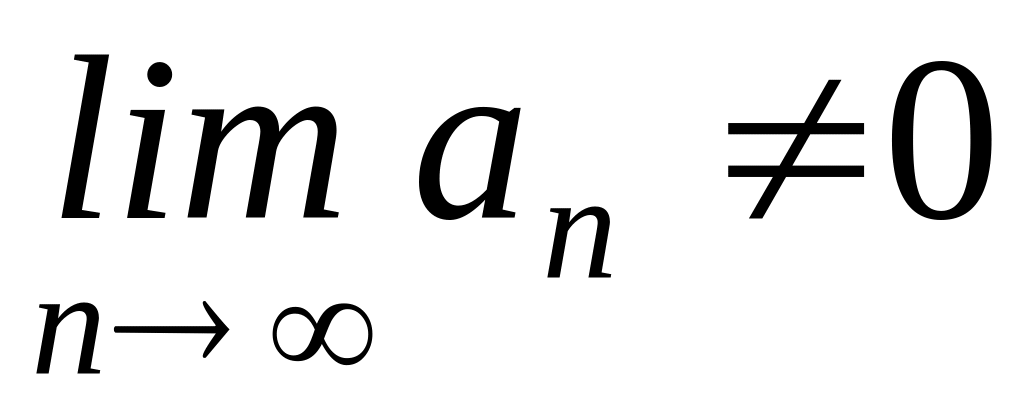

существует конечный предел частичной суммы, т.е.
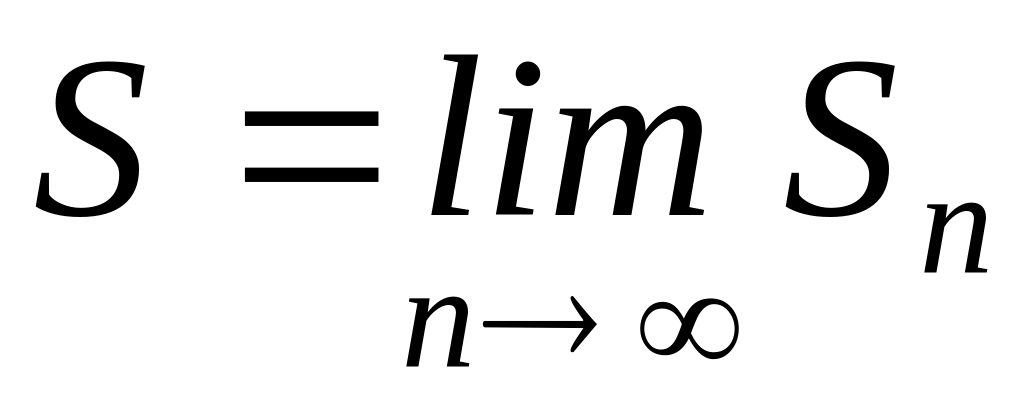
частичная сумма не ограничена
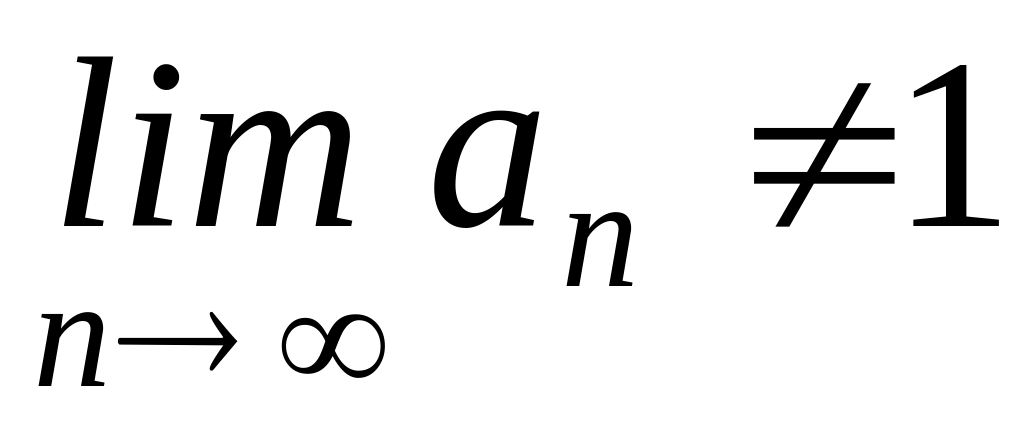
12. Ряд называется расходящимся, если
 конечный
конечныйчастичная сумма ограничена
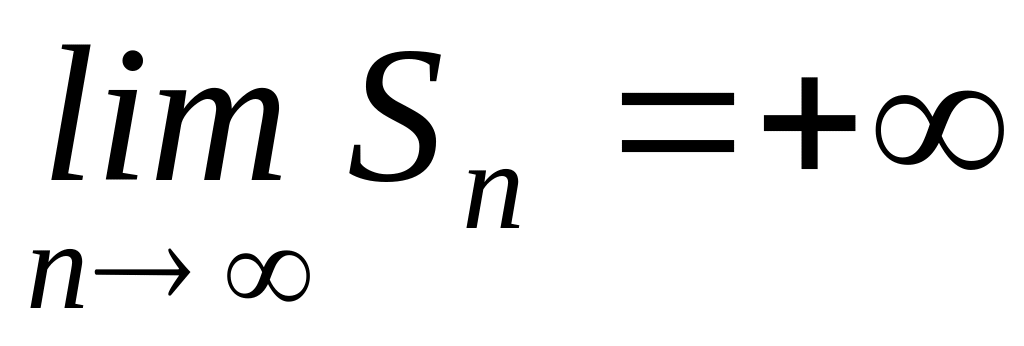 ,
,
 или предел частичной суммы не существует
или предел частичной суммы не существует

13. Если ряд сходящийся, то
для
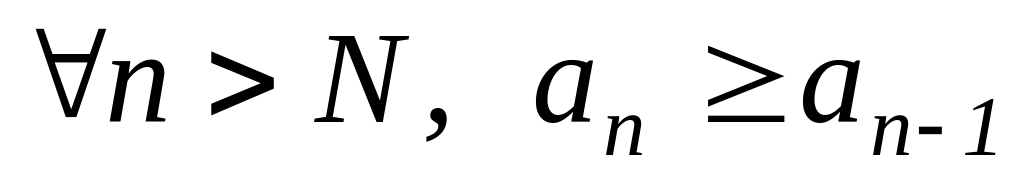


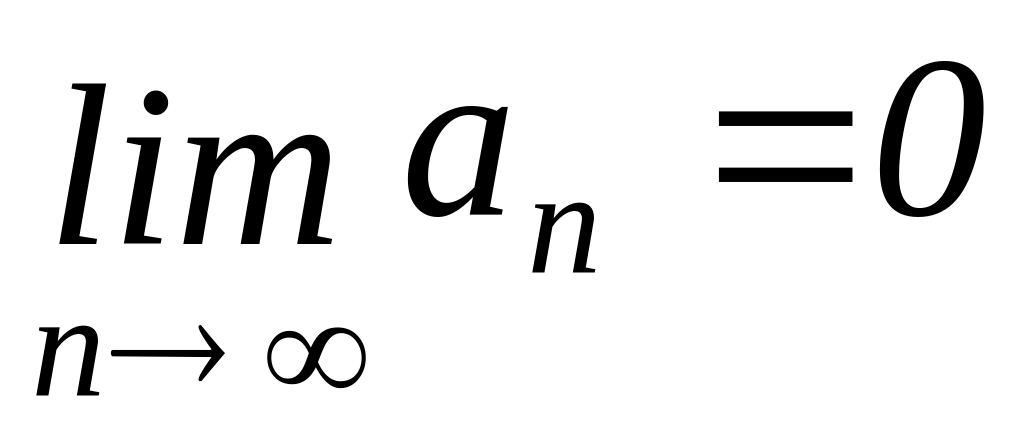
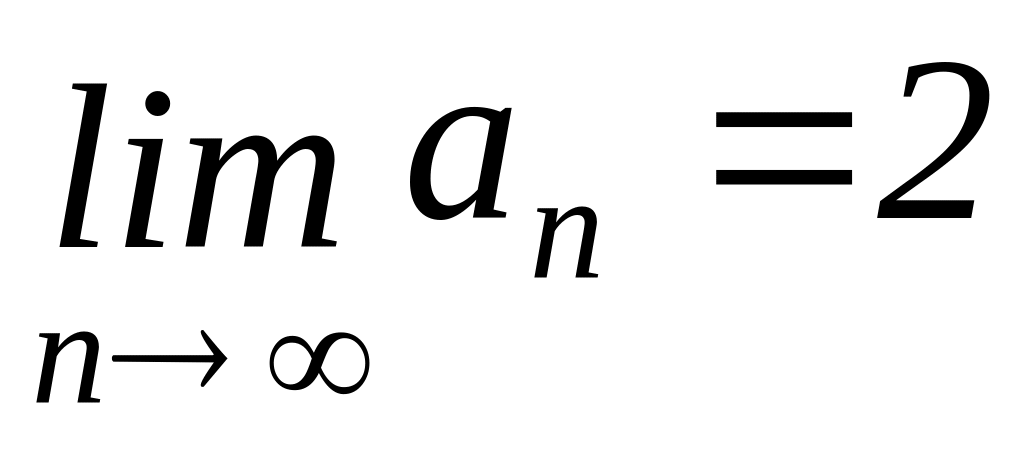
14.
Какое условие является достаточным для
расходимости ряда![]() ?
?
15.
Знакоположительный ряд
![]() является сходящимся по признаку
Даламбера, если
является сходящимся по признаку
Даламбера, если
16. Знакоположительный ряд является расходящимся по признаку Даламбера, если
17.
Знакоположительный ряд
![]() является
сходящимся по признаку Коши, если
является
сходящимся по признаку Коши, если
18.
Знакоположительный
ряд
![]() является
расходящимся по признаку Коши, если
является
расходящимся по признаку Коши, если
19.
Знакоположительный ряд
![]() будет сходящимся, если при сравнении
со сходящимся знакоположительным рядом
будет сходящимся, если при сравнении
со сходящимся знакоположительным рядом
![]() выполняется условие
выполняется условие
20.
Знакоположительный ряд
![]() будет расходящимся, если при сравнении
с расходящимся знакоположительным
рядом
будет расходящимся, если при сравнении
с расходящимся знакоположительным
рядом
![]() выполняется условие
выполняется условие
21. Знакоположительный ряд будет сходящимся, если при сравнении со сходящимся знакоположительным рядом выполняется условие
22.
Какое условие является достаточным для
сходимости ряда
![]() ?
?
23.
Члены ряда
![]() положительны и для
положительны и для
![]() и
и
![]() ,
где
,
где
![]() –непрерывная
невозрастающая функция. Тогда, если
несобственный интеграл
–непрерывная
невозрастающая функция. Тогда, если
несобственный интеграл
![]() сходится, то
сходится, то
ряд расходится
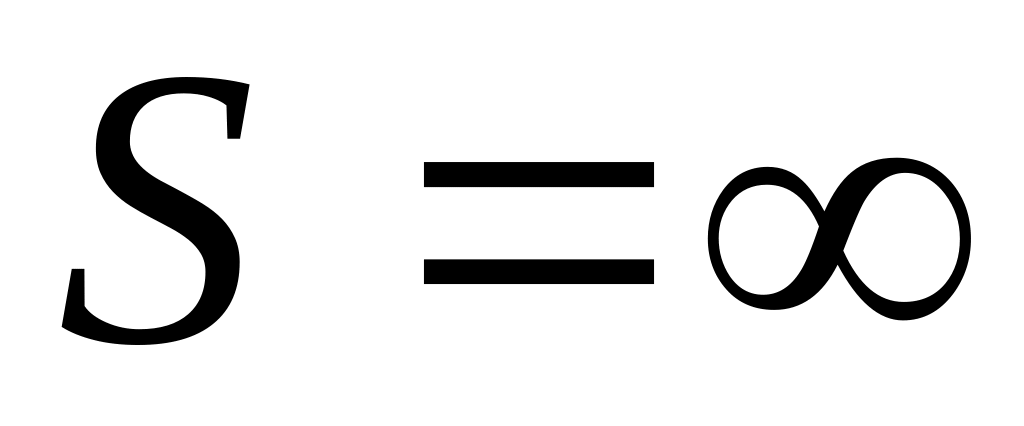
ряд абсолютно сходится
ряд сходится
ряд условно сходится
24.
Укажите ряд Тейлора функции
![]() в окрестности точки
в окрестности точки
![]()
25.
Укажите формулу Тейлора функции
в окрестности точки
(![]() - остаточный член формулы Тейлора)
- остаточный член формулы Тейлора)
26.
Члены ряда
![]() полождительны и для
полождительны и для
![]() и
и
![]() ,
где
непрерывная
невозрастающая функция. Тогда, если
несобственный интеграл
,
где
непрерывная
невозрастающая функция. Тогда, если
несобственный интеграл
![]() сходится, то
сходится, то
Ряд расходится
Ряд сходится
Ряд абсолютно сходится
Ряд условно сходится
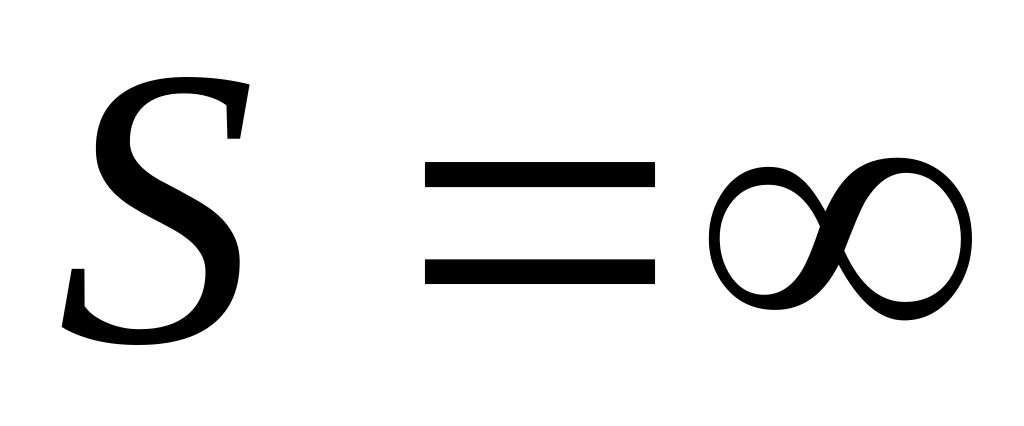
27. Члены ряда полождительны и для и , где непрерывная невозрастающая функция. Тогда, если несобственный интеграл расходится, то
Ряд условно сходится
Ряд сходится
Ряд абсолютно сходится
Ряд расходится
28.
Функция
![]() называется непрерывной в точке
называется непрерывной в точке
![]() ,
если
,
если
Частные призводные первого порядка равны
Существует конечный предел частичной суммы
Предел функции в этой точке существует и равен значению функции в этой точке
Частичная сумма не ограничена

29.
Дано
и
![]() .Если
существует предел
.Если
существует предел
![]() ,
то он называется
,
то он называется
Частной производной функции по переменной
Смешанной производной
Полный дифференциал
Частной производной функции по переменной
Неявной
30.
Дано
и
![]() .Если
существует предел
.Если
существует предел
![]() ,
то он называется
,
то он называется
Полный дифференциал
Смешанной производной
Частной производной функции по переменной
Частной производной функции по переменной
Неявной
31.
Знакопеременный ряд
![]() называется условно сходящимся, где
члены ряда
называется условно сходящимся, где
члены ряда
![]() как
положительные, так и отрицательные,
если:
как
положительные, так и отрицательные,
если:
