Перевод правильных дробей

В этом случае выражение для А_p и А_d будут выглядеть:

A_p = a_-1p^-1 + a_-2p^-2 + … + a­­_-mp^-m

A_d = b_-1d^-1 + b_-2d^-2 + … + b­­_-md^-m

где a_i и b_i – цифры p-чной и d-чной систем.

Приравняем выражения. A_d = A_p = b_-1d^-1 + b_-2d^-2 + … + b­­_-md^-m

Для определения b_-1 умножим обе части равенства на число d, при этом в левой части пользуемся p-чной арифметикой. A_p*d

Выделим в А_p*d целую и дробную часть. Учитывая, что b_i меньше или равна d-1 и больше или равна 0, приравняем между собой целые и дробные части. В результате чего получим:

{A_p*d}_цел = b_-1

К оставшейся правой дробной части применим тот же алгоритм, в результате него найдем b_-2, и так далее, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в d-чной системе счисления.

Так как все операции выполняются в p-чной системе, то в этой же системе будут найдены коэффициенты b_i, поэтому их необходимо будет записать d-чной цифрой. Чаще всего это правило используется для преобразования правильных дробей из десятичной в любую другую СС. Таким образом, представление дробной части числа А_p в d-чной системе будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных d-чной цифрой. Если требуемая точность перевода числа А_p составляет j знаков после запятой, то предельная абсолютная погрешность равняется выражению 3)

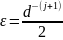
Пример.

Перевести 0.2 в двоичную систему счисления.

0.2*2=0.4 (0)

0.4*2=0.8 (0)

0.8*2=1.6 (1)

0.6*2=1.2 (1)

И так далее.

Если десятичная дробь является точным числом, то в результате перевода в двоичную систему получаем периодическую дробь. (0.0011)₂ здесь в скобках указан период дроби.

Перевести 0.36 в 8-чную.

0.36*8=2.88 (2)

0.88*8=7.04 (7)

0.04*8=0.32 (0)

А₈=0.270 с заданной точностью.

Особое внимание заслуживает случай перевода из p-чной в d-чную, когда основание связаны равенством p=d^k , где к – положительное число.

Правила перевода:

В исходной d-чной записи числа переводим из d-чной в p-чную, разряды объединяются вправо и влево от точки в группы длиной k. Если нужно левее старшей и правее младшей значащих цифр добавляем нужное кол-во нулей. И каждая группа записывается одной p-чной цифрой.

Обратный перевод из p в d: каждая цифра из p-чной заменяется ее d-чным изображением.

(01 21 21 12)₄ = 1996₁₆

2-чная, 8-чная и 16-чная системы счисления.

Именно они используются в ЭВМ, так как имеют ряд преимуществ перед другими системами. Их реализация – иметь устройство с двумя устойчивыми состояниями, что дает возможность использования булевой алгебры для выполнения логических операций над информацией. Так же легко реализуются арифметические операции.

Единственный недостаток – быстрый рост числа разрядов для записи больших чисел. В случае ручного кодирования информации составления программ на машинном языке используют 8-чную и 16-чную систему счисления.

В этих системах числа считаются достаточно легко и требуют соответственно в три (для восьмеричной) и в 4 (для шестнадцатеричной) раза больше разрядов, чем для 2-чной. При этом перевод осуществляется так же достаточно просто.

Правила выполнения арифметических операций.

В 2-чной 8-чной и 16-чной системах такие, как и в 10-чной, только нужно пользоваться своими для каждой системы таблицами сложения и умножения.

Двоично-десятичная система.

Она используется в том случае, когда основная часть операций связана не с обработкой и хранением вводимой информации, а с её вводом и выводом на какие-либо индикаторы с десятичным представлением полученных результатов. Например, калькуляторы, кассовые аппараты. В двоично-десятичной системе десятичные цифры от 0 до 9 представляются как 0000 и 1001, то есть двоичным эквивалентом десяти первых 16-чных цифр.

Преобразование из двоично-десятичной в десятичную систему и обратно выполняется путем прямой замены четырех двоичных цифр одной десятичной. Две двоично-десятичные цифры составляют один байт. Таким образом, с помощью одного байта в двоично-десятичной системе можно представить числа от 0 до 99 (если это рассмотреть как 8-разрядное двоичное число – то диапазон от 0 до 255). Используя один байт для представления каждых двух десятичных цифр можно формировать двоично-десятичные числа с любым требуемым числом десятичных разрядов. Например, 1001 0101 0011 1000 – если его рассматривать как двоичное, то его десятичный эквивалент 38200. Это в несколько раз больше десятичного эквивалента двоично-десятичного числа (9538). Сложение двоично-десятичных чисел, имеющих один десятичный разряд, выполняется так же, как и сложение четырехразрядных двоичных чисел без знака за исключением случая, когда результат превышает 9 (1001). В этом случае необходимо производить коррекцию, которая осуществляется прибавлением к полученному результату двоичного кода числа 6 (0110). Например, 5+9=14 0101+1001=1110 1110+0110=10100 0001 0100

Если первоначальное двоичное сложение или прибавление корректирующего числа приводит к возникновению переноса, то при сложении многоразрядных двоично-десятичных чисел перенос осуществляется в следующий десятичный разряд.

1889+6376=8256

0001 1000 1000 1001 + 0110 0011 0111 0110 = 0111 1011 1111 1111

0111 1011 1111 1111 + 0000 0110 0110 0110 = 1000 0010 0110 0101