Генетичний метод навчання нейронної мережі

Back Propagation.

Цей алгоритм є алгоритмом глобальної оптимізації. У ньому використовуються наступні механізми:

1. схрещування батьківських пар (cross-over), генерація нащадків

2. мутація (дія випадкових впливів)

3. природний добір кращих (селекція)

Мета навчання – мінімізація середньоквадратичної помилки

Задається початкова популяція з N особин . Будь-яка особина представляється відповідними вагами. Обчислюємо індекс придатності (Fitness Index) і оцінюємо якість прогнозування

де С - константа.

1. Схрещування батьківських пар. При виборі батьків використовується імовірностний механізм. Позначимо - імовірність вибору i-го батька:

Потім здійснюється схрещування обраних пар. Можна застосовувати різні механізми схрещування. Наприклад:

Для першого нащадка беруться непарні компоненти з вектора першого батька, а парні компоненти з вектора другого батька, для другого нащадка навпаки – парні компоненти з вектора першого батька, а непарні компоненти з вектора другого батька. Це можна записати таки чином:

Береться батьківських пар і генеруються N нащадків.

2. Дія мутацій

де ,

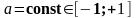
r – початковий рівень мутації, випадкова величина, розподілена рівномірно в інтервалі

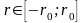
n – номер ітерації

3. Селекція. Можна використовувати різні механізми селекції.

1) Повна заміна старої популяції на нову.

2. Вибір N кращих із всіх існуючих особин за критерієм максимуму FI.

На цьому одна ітерація генетичного алгоритму закінчується.

Описані ітерації повторюємо доти, поки не почне виконуватися одна з наступних умов зупинки:

а) , де - задане значення FI;

б) k  N_зад. , де N_зад. , де N_зад. – задана кількість ітерацій (10³…10⁴)

Основна перевага генетичного метода – це те, що він дозволяє знаходити глобальний мінімум, проте він має такі недоліки:

1. він потребує значних обчислювальних витрат;

2. ряд параметрів визначається експериментально, наприклад:

N – розмір популяції

- показник загасання мутацій.

Градієнтний алгоритм навчання нейронної мережі

Першим алгоритмом навчання, який було розроблено для навчення мережі Back Propagation (ВР), являвся градієнтний метод навчання.

Нехай критерій навчання мережі, що має 3 шари (один прихований шар), такий

де - бажане значення і-го виходу нейромережі,

- фактичне значення і-го виходу нейромережі ВР, для вагової матриці .

Тобто критерій являє собою середній квадрат помилки апроксимації.

Нехай функції активації для нейронів прихованого шару та нейронів вихідного шару - однакові і представляють собою функцію “сигмоїд”

Для такої функції похідна дорівнює:

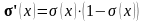
Розглянемо градієнтний алгоритм навчання нейронної мережі.

1. Нехай - поточне значення матриці ваг. Алгоритм має такий вигляд:

,

де 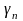- розмір кроку на -й ітерації.

2. На кожній ітерації спочатку ми навчаємо (коригуємо) вхідні ваги.

3. Знаходимо (навчаємо) вихідні ваги

де - входи НМ,

- виходи НМ,

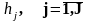- виходи прихованого шару.

4. та переходимо на наступну ітерацію.

Зауваження: Так званий алгоритм навчання з пам’яттю має вигляд:

, де

- швидкість навчання, - параметр забування.

Градієнтний метод є першим запропонованим алгоритмом навчання, він простий в реалізації, але має такі недоліки:

• повільно збігається;

• знаходить лише локальний екстремум.

Удосконалення градієнтного алгоритму навчання нейронної мережі ВР

При реалізації градієнтного алгоритму навчання нейронної мережі ВР може проявитися ряд складностей, властивих градієнтним алгоритмам оптимізації:

1. Якщо ми знаходимося далеко від точки мінімуму функції , то рухаємося з малим кроком, і процес пошуку може затягуватися. Для його прискорення має сенс збільшити величину кроку . Ознакою такої ситуації є сталість знака (Рис 2.1а).

2. Якщо ж ми знаходимося в околиці точки мінімуму , і величина кроку велика, то ми перескакуємо через точку , і виникає явище “осциляції”. У цьому випадку доцільно поступово зменшувати величину . Ознакою такої ситуації є зміна знака , тобто (див. Рис 2.1б).

Рис.1а

Рис.1б