28. Алгоритм мимовільної розбивки на незадане число класів

Нехай - проекція на , . Тоді . Визначивши проекції всіх точок вихідної множини на , приводимо задачу до одномірного випадку. Багатомірність простору зображень враховується при обчисленні дисперсій у підмножинах , а саме

У результаті розбивається рівнобіжними гіперплощинами, що проходять через точки нормально до найбільшого власного вектора матриці . Пороги визначаються відповідно до описаного вище алгоритму.

У зв'язку з тим, що уже після першої розбивки найбільші власні вектори в утворених підмножинах і можуть не співпадати з , недоцільно проводити розбивку в одному напрямку більше, ніж на два класи.

Тому процес розбивки при k>2 варто звести до послідовної дихотомії. Багаторазово застосовуючи алгоритм оптимальної дихотомії, можна одержати розбивку на будь-яке число класів.

Однак алгоритм оптимальної дихотомії сам по собі ще не забезпечує оптимуму при розбивці на k класів. Тому випливає оптимізувати процес розбивки, увівши деякий критерій об'єднання. Цей критерій повинен залежати від і . Нехай після розбивки на k класів і - сусідні підмножини. При об'єднанні і дисперсія може зрости, тому що ,

а функція вартості зменшиться, тому що .

Тому якщо величина менше нуля, то втрати за рахунок збільшення дисперсії компенсуються зменшенням вартості на утримання класів, а тому і доцільно об'єднати. Як критерій об'єднання приймемо відношення . Тоді правило об'єднання можна записати в наступному виді:

- деякий поріг, що залежить від номера кроку. Якщо покладемо Т=1, то правило об'єднання буде діяти, починаючи з першого кроку, після кожної чергової розбивки. У такому випадку процес формування множин закінчується в той момент, коли після деякого об'єднання ми одержимо ті ж самі множини, що були до початку розбивки на цьому кроці.

Ясно, що такий вибір порога не може привести до найкращої розбивки, оскільки залишається можливість застрягти на проміжному мінімумі функціонала вартості, не довівши розбивку до кінця. Можна рекомендувати вибір перемінного порога з наступних міркувань. Оскільки на перших кроках має сенс провести розбивку на можливо більше число класів, поріг Т вибирається <1. Далі процес розбивки повинен перемінитися протилежним процесом – об'єднанням, а тому Т буде зростати від кроку до кроку, поки не досягне свого сталого значення Т=1. (Як функцію можна вибрати, наприклад, , де r – номер кроку.)

Регулюючи величину , можна одержувати різні співвідношення між режимами розбивки й об'єднання класів.

Опишемо коротенько алгоритм формування класів:

а) обчислюється матриця коваріацій вихідної множини;

б) визначаються , і ;

в) знаходимо проекції точок на ;

г) робимо оптимальну дихотомію в напрямку й одержуємо дві підмножини і ;

д) перевіряємо сусідні підмножини (класи) за критерієм об'єднання

30. Агломеративний ієрархічний алгоритм кластер-аналізу

Загальна схема всіх алгоритмів цього класу така: формується послідовність порогів , що зв'язана з побудовою дерева кластеризації. Починається з кластеризації, при якій кожна точка є окремий кластер.

На першому кроці поєднуються ті точки, міра близькості яких не перевищує ,

На другому кроці поєднуються ті, у яких поріг близькості не перевищує і т.д. доти пока всі точки не об'єднаються в один клас, чи на деякому рівні число кластерів буде стабілізовано, і при цьому всі точки усередині класу задовольнятимуть порогові .

Насамперед, для побудови правила останова буде використане поняття мінімальної дистанційної розбивки , де e-еталон .

і при цьому наступний крок

Розбивка називається незміщеною, якщо ця розбивка з точністю до множини міри нуль збігається з мінімальною дистанційною розбивкою породжуваною векторами середніх

де - сукупність точок, що належать ; - число точок в

Правильною кластерізацією називається незміщена розбивка точок вибірки на кластери для якої виконується наступні умови:

1. визначені оцінки середніх

2. найбільша внутрішньокластерна відстань на множині кластерів менше найменшої міжкластерної відстані, тобто

де - відстань між точками одного кластера: - відстань між різними кластерами. може бути визначено різними способами

• як максимальна відстань між парою точок з цих кластерів:

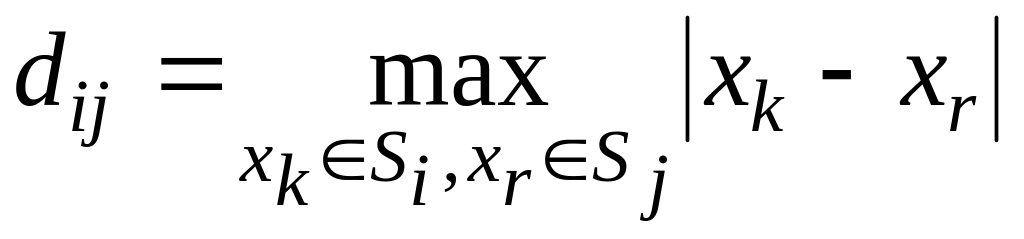
• як відстань між центрами кластерів: 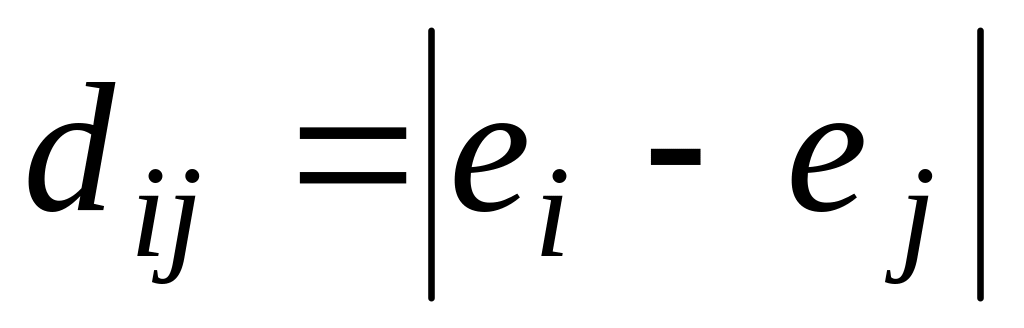, , 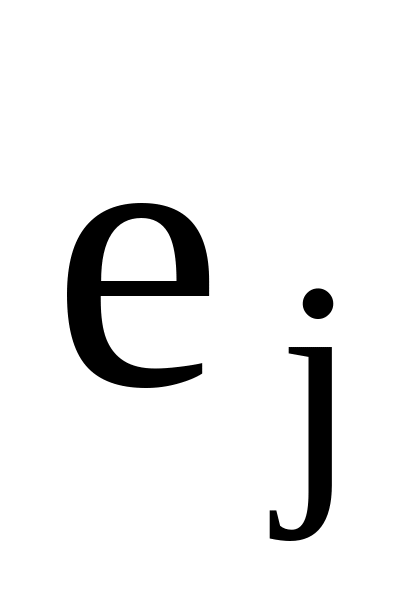аналогічно.

Опис алгоритму кластеризації

Початковий етап

Задано послідовність , початковий набір середніх , де , i=1..N. Початкове розбиття , де , i=1..N,

1-а ітерація:

1. Визначимо розбиття шляхом відшукання точок , найближчих до центра , і їх об'єднання в один клас.

Цей крок повторюємо доти, поки не вийде: , де

- число кластерів отриманих з 1-ої ітерації.

Обчислюємо центри нових кластерів

,

На 2-ій ітерації поєднуємо сусідні кластери, відстань між якими

r-а ітерація (r>1):

Послідовно за рекурентними формулами знаходимо нову розбивку шляхом злиття найближчих кластерів і визначення їх центрів (змінні r-го рівня ієрархії).

- число кластерів, отриманих з r-ої ітерації.

Обчислюємо змінні r-го рівня ієрархії (центри)

Продовжуємо виконувати ітерації доти, поки не почне виконуватися умова (тобто, коли відстань між кожною парою кластерів не стане або всі кластери не зіляються в один).