
- •Повторные пределы.
- •Частные производные функций.
- •Дифференцируемость функции многих переменных в точке.
- •Геометрический смысл частных производных и дифференциалов функции.
- •Дифференцирование сложной функции.
- •Инвариантность формы первого дифференциала относительно выбора переменной. Правило вычисления дифференциала.
- •Производная по направлению. Градиент функций.
- •Частные производные и дифференциалы высших порядков от функций многих переменных.
- •Различные формы остаточного члена в формуле Тейлора для функций одной вещественной переменной.
- •Формула Тейлора для функции многих переменных.
- •- Форма Пеано
- •Локальный экстремум функции многих переменных.
- •Дифференцируемые отображения.
- •Неявные функции и отображения.
- •Условный экстремум функции многих переменных.
- •Метод неопределенных множителей Лагранжа.
- •Достаточное условие условного экстремума.
Инвариантность формы первого дифференциала относительно выбора переменной. Правило вычисления дифференциала.
Теорема:
пусть функции
определены в некоторой окрестности
точки
 и дифференцируемы в точке
.
Пусть
,
где
,
пусть
определена в некоторой окрестности
точки
и дифференцируема в точке
.
Тогда сложная функция
и дифференцируемы в точке
.
Пусть
,
где
,
пусть
определена в некоторой окрестности
точки
и дифференцируема в точке
.
Тогда сложная функция
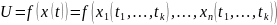 переменных
переменных
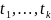 дифференцируема в точке
,
причём для дифференциала этой функции
в этой точке может быть выбран любой
из двух способов записи:
дифференцируема в точке
,
причём для дифференциала этой функции
в этой точке может быть выбран любой
из двух способов записи:
1)
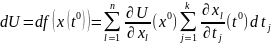
2)

Доказаельство: наша внешняя функция
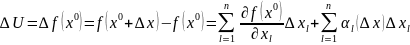




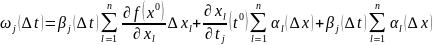
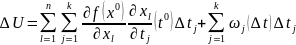
-
это означает, что функция дифференцируема
в точке
,
а в главной линейно части представления
приращения коэффициенты при
 представляют собой производные
представляют собой производные
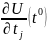

если
учесть, что
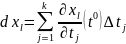 ,
то можно переписать и так:
,
то можно переписать и так:
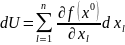
где
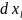 - дифференциал функции.
- дифференциал функции.
Замечание: инвариантность формы первого дифференциала можно понимать следующим образом: для дифференцируемой в точке её дифференциал в точке
в каждом из двух случаев
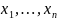 – независимые
переменные, тогда
– независимые
переменные, тогда

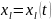 – дифференцируемые
функции, такие, что
– дифференцируемые
функции, такие, что
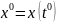 и тогда
и тогда
Свойства инвариантных форм первого дифференциала используемые при практическом вычислении дифференциала и частных производных.
В
частности, если
 и
и
 дифференцируемые функции нескольких
переменных, то имеет место формула:
дифференцируемые функции нескольких
переменных, то имеет место формула:
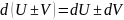

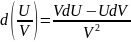
Доказательство:

Используем свойство инвариантности форм первого дифференциала
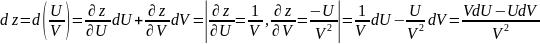
Заметим,
если есть фунция
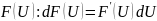
Производная по направлению. Градиент функций.
Пусть
функция
определена в некоторой окрестности
точки
,
пусть
 некоторая точка этой окрестности.
Проведем прямую через
и
некоторая точка этой окрестности.
Проведем прямую через
и
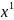 .
Параметрические уравнения этой прямой
будут иметь вид
.
Параметрические уравнения этой прямой
будут иметь вид

Где
 - прямая,
- прямая, - луч
- луч

Заметим,
если разделим
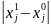 на
на


Это означает, что эти выражения можно считать косинус углов

Углы
 - направляющие углы вектора
- направляющие углы вектора
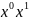 ,
,
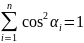
Вектор
с координатами ( - это направление вектора
- это направление вектора
 .
.
Возьмём
точку
 на прямой, соединяющей точки
и
( в векторной форме
на прямой, соединяющей точки
и
( в векторной форме
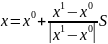 ),
тогда для этой точки будем иметь
),
тогда для этой точки будем иметь

Будем
считать, что точка
фиксирована, а
 - переменная, обозначим через
- переменная, обозначим через
 - направление вектора
,
то есть
- направление вектора
,
то есть

Производная
функции
в точке
по направлению
определяется как производная
 сложной функции
сложной функции
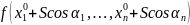
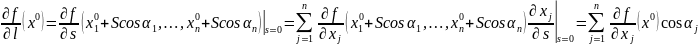
Из частных производных функции можно составить произвольный вектор градиент
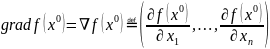
Если
через
обозначить направление вектора
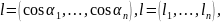 где
где

В этом случае
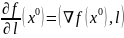
Частные производные и дифференциалы высших порядков от функций многих переменных.
Пусть функция определена в некоторой окрестности точки в пространстве и имеет в
Этой
окрестности частную производную
 ,
которая представляет собой некоторую
функцию, определенную в окрестности
точки
.
Предположим, что эта новая функция
в точке
имеет частную производную по переменной
,
которая представляет собой некоторую
функцию, определенную в окрестности
точки
.
Предположим, что эта новая функция
в точке
имеет частную производную по переменной
 ,
она обозначается
,
она обозначается

и
называется производной второго порядка
по переменным
 .
.
Если
 ,
то частная производная второго порядка
называется смешанной.
,
то частная производная второго порядка
называется смешанной.
Если
 ,
то
,
то

Заметим, что в общем случае порядок, в котором вычисляются смешанные производные играет существенную роль для результата, который получится.
Теорема
(о равенстве смешанных производных):
Пусть функция
определена вместе со своими частными
производными
 в некоторой окрестности точки
,
причём смешанные частные производные
второго порядка
в некоторой окрестности точки
,
причём смешанные частные производные
второго порядка
 непрерывны в точке
,
тогда
непрерывны в точке
,
тогда
 .
.
Доказательство:
введём в рассморение вспомагательную
функцию
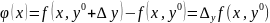

Далее введем в рассморение
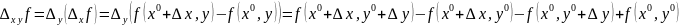

Мы
получили
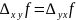
Применим
к каждому из приращений
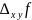 и
и
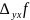 формулу конечных приращений Лагранжа:
формулу конечных приращений Лагранжа:
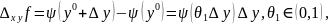
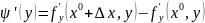
Таким образом
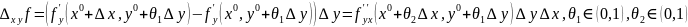
Аналогично получаем

Получили
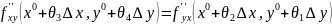
Переходим
к пределу
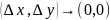
В
силу непрерывности
 и
и
 в точке
при этом переходе к пределу получим:
в точке
при этом переходе к пределу получим:
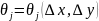 ,
поэтому
,
поэтому
 и
и
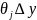 стремится к 0 при
стремится к 0 при
 и
и
 .
.
Замечание: по индукции утверждение этой теоремы можно распросронить и на смешанные частные производные более высоких порядков.
Определение: пусть определена в некоторой окрестности точки и дифференцируема во всех точках этой окрестности, тогда её дифференциал

является
функцией от
 переменных:
и
переменных:
и
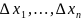 .
.
При фиксированных приращениях этот дифференциал представляет собой функцию переменных определенную в октрестности точки .
Предположим,
что эита функция
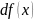 дифференцируема в точке
(как функция перемнной
при фиксированных
дифференцируема в точке
(как функция перемнной
при фиксированных
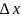 ),
тогда говорят, что функция
дважды дифференцируема в точке
),
тогда говорят, что функция
дважды дифференцируема в точке
 При этом дифференциал от её дифференциала
,
вычесленный в точке
,
при условии, что переменные получают
те же самые фиксированные приращения
,
называется вторым дифференциалом в
точке
или дифференциалом второго порядка о
обозначается
При этом дифференциал от её дифференциала
,
вычесленный в точке
,
при условии, что переменные получают
те же самые фиксированные приращения
,
называется вторым дифференциалом в
точке
или дифференциалом второго порядка о
обозначается
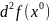 .
.
Аналогично определяются дифференциалы более высоких порядков.
Пусть
функция
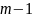 раз дифференцируема в окрестности
точки
,
тогда её дифференциал
раз дифференцируема в окрестности
точки
,
тогда её дифференциал
 при фиксированных приращениях
является функцией переменных
,
определенной в окрестности точки
.
Предположим, что функция
дифференцируема в точке
при фиксированных приращениях
является функцией переменных
,
определенной в окрестности точки
.
Предположим, что функция
дифференцируема в точке
 тогда про функцию
говорят, что она
тогда про функцию
говорят, что она
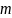 раз дифференцируема в окрестности
точки
,
а дифференциал от её дифференциала
порядка
,
вычисленный в точке
при условии, что полученный приращения
такие же, как и при вычислении всех
дифференциалов до порядка
(включая), называется дифференциалом
порядка
и обозначается
раз дифференцируема в окрестности
точки
,
а дифференциал от её дифференциала
порядка
,
вычисленный в точке
при условии, что полученный приращения
такие же, как и при вычислении всех
дифференциалов до порядка
(включая), называется дифференциалом
порядка
и обозначается
 .
.

Выведем формулу для вычисления второго порядка:

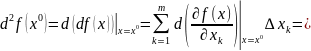
Пусть функция в точке имеет непрерывную частную производную второго порядка

Введем в рассмотрение формальные символы:
 – производная
функции
по
– производная
функции
по
 ,
,

Будем считать произведение – суперпозицией операций, для функций, имеющих частные непрерывные производные.


Далее аналогично по индукции можно доказать, что если имеет в точке непрерывные частные производные порядка , то для дифференциала порядка имеет место равенсво:

В частности

Если функция имеет в точке (области) непрерывные частные производные до порядка (включая), то говорят, что она непрерывно дифференцируема в этой точке (области).
В отличии от первого дифференциала, дифференциалы более высоких порядков не обладают свойством инвариантности форм.
