Дифференциальное исчисление функций многих переменных.

Некоторые эффекты, связанные с пределами функций многих переменных.

Пусть отображение 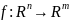, которое задано на множестве 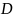в пространстве 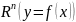Пусть 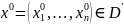, элемент называется пределом отображения в точке по множеству

если:

По Коши:

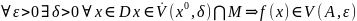
По Гейне:

Если множество 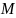совпадает с областью определения отображения , то мы опускаем слова «по множеству » .

Очевидно, что если , то по любому множеству предел отображения тоже будет равен . Часто в качестве таких подмножеств рассматривают непрерывные кривые, имеющие конец , в этом случае пределом по множеству называют предел по кривой . Или же лучи, с концами в точке , в этом случае говорят, что предел по множеству является предел по направлению соответствующего луча. Если в точке существует предел , то по любому направлению в точке предел будет равен

Из существования предела функции в точке по любому направлению не следует, что в этой точке у функции имеется предел по всей области определения.

Повторные пределы.

На ряду с рассматриваемыми пределами можно рассматривать и повторные пределы, связанные с последовательным переходом к пределу по различным координатам или по более сложным множествам. Рассмотрим следующую функцию от двух переменных. Пусть 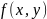определена на множестве , 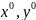– предельные точки множества . Предположим, что существует

Для некоторых допустимых , так, чтобы и

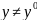
Тогда

- повторный предел.

Аналогично определяется .

В общем случае повторный предел и предел функции многих переменных не связаны между собой. При некоторых дополнительных условиях связь отслеживается.

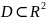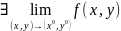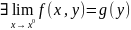Теорема: пусть определена на множестве , а множество содержит некоторую прямоугольную окружность точки , кроме, может быть, самой этой точки, , кроме того на числовой прямой , тогда

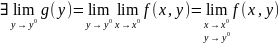
Доказательство: пусть . Зафиксируем произвольное . Согласно определению Коши предел функции в точке, найдётся некоторая проколотая окрестность точки такая, что для любой точки , которая принадлежит этой окрестности в пересечении с выполняется неравенство

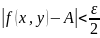
В силу теоремы о вложенных окрестностях без ограничения общности можно считать, что указанная окрестность точки является прямоугольной:

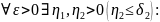
В неравенстве перейдём к пределу при . Пределы справа и слева существуют:

Получили: - это и означает, что

Частные производные функций.

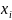Пусть определена в некоторой окрестности точки . Частной производной от функции по переменной в точке называется следующий предел:

Стоящая в числителе разность иногда называют частичным приращением по переменной в точке .

Из этого определения: для вычисления частной производной по какой-либо переменной мы должны представить, что остальные зафиксированы и постоянны. В результате получаем функцию от одной переменной и от неё берём производную.

Отметим, что из существования частных производных функций в точке по всем переменным не следует непрерывность функции в этой точке.

Дифференцируемость функции многих переменных в точке.

Определение: пусть функция определена в некоторой окрестности точки в пространстве 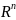. Пусть каждая из переменных получает приращение 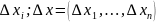; ; 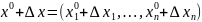тогда будем считать, что точка 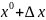так же находится в указанной окрестности точки . Полным приращением функции 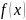будем называть такую разность

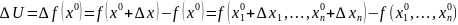
Определение: функция 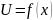определенная в некоторой окрестности точки называется дифференцируемой в точке , если в некоторой окрестности точки полное приращение этой функции может быть представлено в виде:

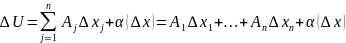
где - некоторые числа (определяются функцией и точкой , но не зависят от приращения переменной), функция представима в виде

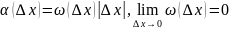
Из определения: 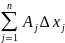является главной линейной частью приращения 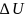; если это приращение рассматривать как функцию 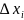, эта линейная часть приращения называется дифференциалом функции в точке :

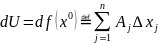
Далее, как и в случае функции одной переменной, по определению будем считать, что дифференциалы независимых переменных совпадают с их приращением: .

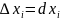Лемма:

Доказательство: I) над уравнением произведем следующее , где 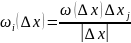, - бесконечно малая

Докажем, что – ограниченная:

Значит - бесконечно малая.

II)

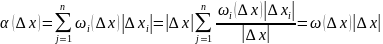
- бесконечно малая, – ограниченная.

Так как 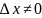, то будем полагать .

Теорема: если функция дифференцируема в точке, то она непрерывна в этой точке.

Доказательство: если дифференцируема в точке , то в некоторой окрестности , если перейдём к пределу, получим 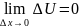, что и означает непрерывность в точке .

Теорема: если функция дифференцируема в точке, то она имеет в этой точке частные производные (конечные) по всем переменным, при этом

где - коэффициенты дифференциала.

Доказательство: рассмотрим

так как это частный случай полного дифференциала, так что её приращение можно представить:

Тогда

Эти теоремы позволяют сделать следующий вывод: непрерывность и наличие частных производных являются необходимыми условиями дифференцирования.

Теорема (достаточное условие дифференцирования функции многих переменных): пусть функция определена в некоторой окрестности точки и имеет в этой окрестности частные производные 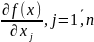, которые непрерывны в точке , тогда функция дифференцируема в точке .

Доказательство: доказательство проведем для случая трёх переменных. Пусть вектор приращений 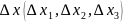такое, что точка

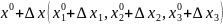
Каждая разность в квадратных скобках может рассматриваться как приращение функции одной переменной, так как остальные фиксированы. К каждой из этих разностей можно применить теорему Лагранжа о конечных приращениях, согласно которой

Мы представляем приращение функции в виде

где

Поскольку по теореме о промежуточной функции 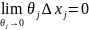. По этому по теореме о пределе сложной функции в силу непрерывности всех частных производных в точке мы получаем . Отсюда следует, что функция дифференцируема в точке . Теорема доказана.Утверждение, обратное этой теореме неверно: из дифференцируемости функции в точке следует существование частных производных в этой точке, но не следует их непрерывность в этой точке.

Если функция имеет в точке (области) непрерывные частные производные по всем переменным, то говорят, что она непрерывно дифференцируема в этой точке (области).