Задача 6.

В целях изучения норм расхода сырья на единицу продукции из партии изделий проведена 2%-ная механическая выборка, в результате которой получено следующее распределение:

Расход сырья, г	Изготовлено изделий, шт.
До 20	8
20-22	15
22-24	50
24-26	20
Свыше 26	7
Итого:	100

Определите:

Применяя способ «моментов»:

а) средний расход сырья на одно изделие;

б) дисперсию и среднее квадратическое отклонение;

Коэффициент вариации;
С вероятностью 0954 - возможные пределы расхода сырья на единицу продукции для всей партии изделий.

Решение:

Чтобы определить числовые характеристики заданного статистического распределения, перейдем к условным вариантам по формулам:

X_i= (X_max – X_min) – среднее значение интервалов

А – ложный ноль

К – величина интервала

В качестве ложного нуля возьмем значение х_i, соответствующее наибольшей частоте f_i.

Наибольшая частота f_i= 50, тогда А = х₄ = 23 – условная средняя, k=2.

Приведем группировку к стандартному виду с равными интервалами и найдем середины интервалов для каждой группы.

Расход сырья, г x_min,x_max	Изгоовлено изделий,шт f_i	xi	Xi -A	(x_i – A)/k	((x_i– A)/k)*f_i
до 20	8	19	-4	-2	-16
20-22	15	21	-2	-1	-15
22-24	50_max	23_A	0	0	0
24-26	20	25	2	1	20
свыше 26	7	27	4	2	14
Итого	100	-	-	-	3

В статистике ((x_i– A)/k) называется моментом I порядка и обозначается m₁ и рассчитывается по формуле:

M₁= (∑(((x_i– A)/k)*f_i )/∑f =3/100 =0,03

а) найдем средний расход сырья на одно изделие по формуле:

x_cp=m1*k + A

x_cp= 0,03*2 +23=23,06 (г)

б) найдем дисперсию по формуле:

²=(∑(xi – x_cp)² *f_i)/∑f_i

² = 379,43 /100= 3,79 (г)

xi – x_cp	(xi – x_cp)²	(xi – x_cp)² *f_i
-4,06	16,48	131,84
-2,06	4,24	63,6
-0,06	0,003	0,15
1,94	3,76	75,2
3,94	15,52	108,64
	Итого:	379,43

Найдем среднее квадратичное отклонение:

Найдем коэффициент вариации:

ﮞ=( /х)*100

ﮞ=(1,94/23,06)*100=8,4%

С вероятностью 0,954 найдем предельную ошибку выборки и возможные пределы расхода сырья на единицу продукции для всей партии изделий.

Р = 0,954; t= 2,0

Возможные пределы найдем по формуле:

, где t- коэффициент доверия, зависящий от вероятности, с которой можно гарантировать, что предельная ошибка не превышают t-кратную ошибку.

x_cp=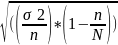 , где n – численность единиц выборочной совокупности, ² – дисперсия варьирующего признака в генеральной совокупности, N – численность единиц в генеральной совокупности, n/N – доля отобранных единиц в генеральной совокупности.