25. Виды дисперсий и правила их сложения.

Изучение вариации (колеблемости, рассеивания) признака по всей совокупности в целом, предусматривает изучение вариации для каждой из составляющих ее групп, а также  между этими группами. В простейшем случае, когда совокупность разбита на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей, межгрупповой и внутригрупповой.

Общая дисперсия D(x) измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака (х_i) от общей средней величины и может быть вычислена как: 1. простая дисперсия   2. взвешенная дисперсия

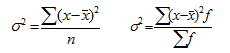
Межгрупповая дисперсия (факторная) характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних  от общей средней:

Внутригрупповая дисперсия (частная, остаточная, случайная)  отражает случайную вариацию неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы (х_i) от средней арифметической этой группы (x_ср) (групповой средней) и может быть исчислена как:

1. простая дисперсия  2. взвешенная дисперсия

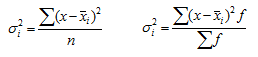
На основании внутригрупповой дисперсии по каждой группе  можно определить общую среднюю из внутригрупповых дисперсий:

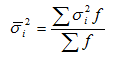
Правило сложения дисперсий

Согласно правилу сложения дисперсий, общая дисперсия равна сумме средней из внутригрупповых

И межгрупповой дисперсий.

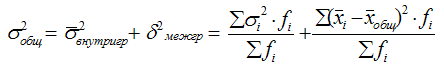
Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью – неизвестную. Чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак. Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации - показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:

При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи – единице. Эмпирическое корреляционное отношение (см. пример) – это корень квадратный из эмпирического коэффициента детерминации:

26. Понятие о рядах динамики, сопоставимость статистических величин в рядах динамики.

Ряды динамики – статистические данные, отображающие развитие во времени изучаемого явления. Их также называют динамическими рядами, временными рядами.

В каждом ряду динамики имеется два основных элемента:

показатель времени t ;

соответствующие им уровни развития изучаемого явления y;

Несопоставимость уровней ряда может возникнуть вследствие из­менения единиц измерения или единиц счета. На сопоставимость уровней ряда динамики непосредственно влияет  методология учета или расчета показателей. Условием сопоставимости уровней ряда динамики является пе­риодизация динамики.

Процесс выделения однородных этапов развития рядов динамики  носит название периодизации динамики.

Важно также, чтобы в ряду динамики интервалы, или моменты, по которым определены уровни, имели одинаковый экономический смысл.

Условием сравнимости уровней интервального ряда является на­личие равных интервалов, по которым даны уровни. Совершенно оче­видно, что нельзя сравнивать квартальную продукцию с годовой.

Уровни ряда динамики могут оказаться несопоставимыми по кругу охватываемых объектов вследствие перехода ряда объектов из одно­го подчинения в другое.

Несопоставимость уровней ряда может возникнуть вследствие изменения территориальных границ областей, районов и т.д.

Приведение уровней ряда к сопоставимому виду. Данный прием осуществляется методом смыкания рядов динамики. Под смыка­ем понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или разным территориальным границам.

Приведение рядов динамики к одному основанию. Т.е. к одному и тому же периоду или моменту времени, уровень которого принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему.

Коэффициент опережения (замедления):  или