2.3 Вычисление эмпирических моментов

Выборке соответствует дискретное распределение (таблица 2.4).

Таблица 2.4

Значения xi	x1	x2	…	xk
Частоты			…

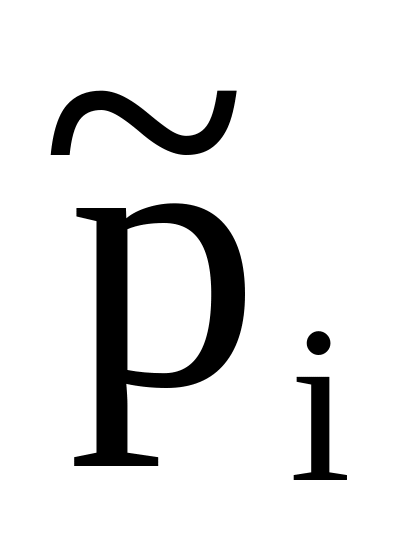
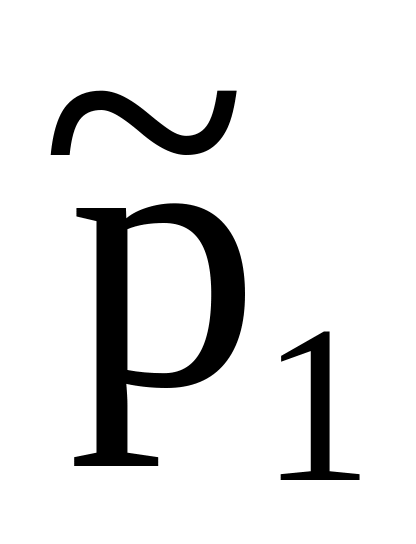
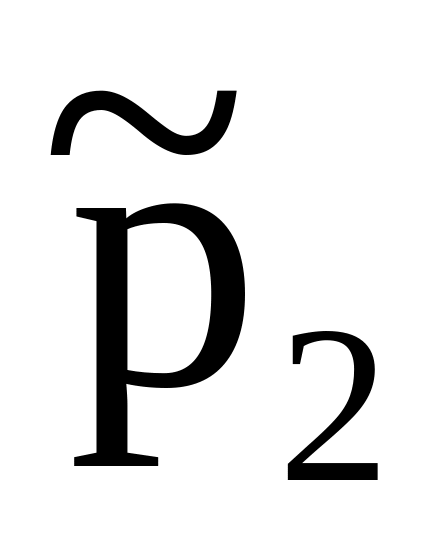
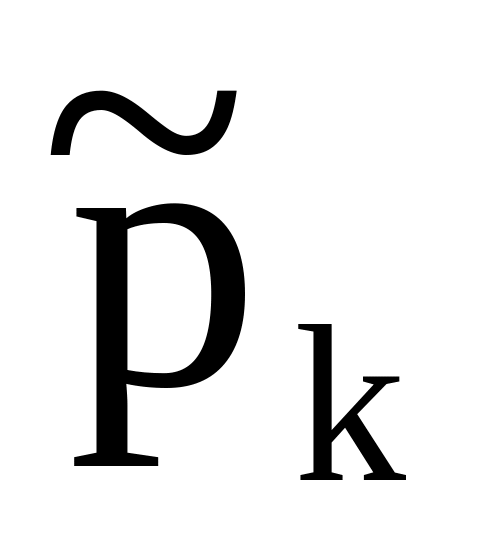
В случае, если выборка задана вариационным рядом, эта таблица имеет следующий вид (таблица 2.5):

Таблица 2.5

Значения xi	x1	x2	…	xn
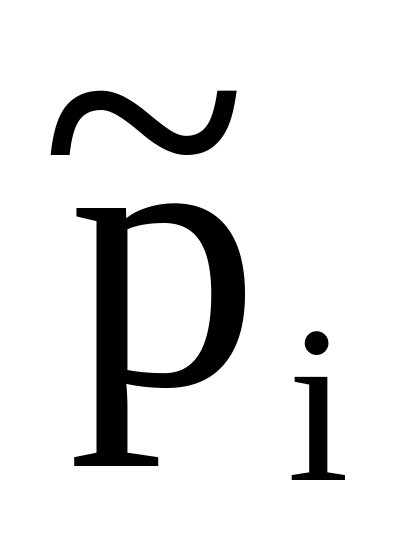
Частоты	1/n	1/n	…	1/n

Вычисление моментов эмпирического распределения согласно таблице 2.6 производится по следующим формулам (во всех формулах n – объем выборки):

Таблица 2.6

	Вариационный ряд общего вида	Вариационный ряд задан таблицей
Начальный эмпирический момент порядка l
Центральный эмпирический момент порядка l

Сравнение с таблицей 1.9 показывает, что первый начальный момент или математическое ожидание выборки а₁ – это введенное нами ранее среднее значение выборки, которое мы обозна-чили через . Выборочную дисперсию b₂ мы назвали разбросом выборки и обозначили S².

Таким образом, согласно методу моментов оценкой для математического ожидания генераль-ного распределения надо взять , оценкой для дисперсии – S². Формулы для их расчета содер-жатся в таблице 1.9.

Пример 2.6. Число неправильных соединений на телефонной станции имеет пуассоновское распределение. В течение часа каждую минуту фиксировали число неправильных соединений, имевших место в эту минуту. Полученные данные представлены в таблице (см. пример 1.4). Оценить среднее число неправильных соединений в час.

Решение. На языке теории вероятностей по результатам выборки надо получить оценку математического ожидания, то есть параметра l распределения Пуассона. Согласно методу момен-тов в качестве оценки для среднего числа неправильных соединений в минуту надо взять:

Согласно правилу устойчивости распределения Пуассона, упомянутому нами ранее, среднее число неправильных соединений в час в 60 раз больше среднего числа неправильных соединений в минуту. Следовательно, оценкой для среднего числа неправильных соединений в час является значение 

2.4. Свойства точечных оценок

Для того чтобы оценка неизвестного параметра, т.е. статистика (x₁,...,x_n) (коротко мы ее будем обозначать _), давала хорошее приближение неизвестного параметра  распределения генеральной совокупности F(x,), желательно, чтобы она удовлетворяла следующим требованиям.

Математическое ожидание оценки параметра по всевозможным выборкам данного объёма должно равняться истинному значению определяемого параметра:

M(_n) = 

В этом случае оценку называют несмещённой. В противном случае оценку называют смещённой.

Если это требование не выполняется, то оценка _n, полученная по разным выборкам, будет в среднем либо завышать, либо занижать значение . К сожалению, часто практически важные оценки являются смещенными, хотя и слабо. Для оценки, смещенной слабо:

M(_n (при n, стремящемся к ).

Было бы ошибочным считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого параметра. Чем больше дисперсия оценки, тем больше ее значения рассеяны вокруг ее среднего значения и, следовательно, удалены от значения оцениваемого параметра. По этой причине к оценке предъявляется требование эффективности.

Оценка называется эффективной, если при заданном объеме выборки n она имеет наимень-шую дисперсию.

При увеличении объёма выборки оценка должна сходиться по вероятности к истинному значению параметра; в этом случае оценку называют состоятельной.

Для состоятельных оценок значительные ошибки при оценивании маловероятны.

Если дисперсия несмещенной оценки при n, стремящемся к бесконечности, стремится к нулю, то такая оценка оказывается и состоятельной. Это непосредственно вытекает из неравенства Чебышева:

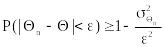
Из неравенства Чебышева видно, что, для того чтобы доказать несмещенность и состоя-тельность оценки, достаточно изучить ее математическое ожидание и дисперсию. Следует заме-тить, что на практике часто для простоты расчетов используют незначительно смещенные оценки или оценки, обладающие большей дисперсией по сравнению с эффективными оценками.

Оценки метода моментов обычно состоятельны, но не являются “наилучшими” в смысле эффективности. Тем не менее метод моментов часто используется на практике, так как вычисления сравнительно просты.