3. Алгоритм розв’язування задач. Приклади задач

3.1. Алгоритм розв’язування задач на знаходження енергії зв’язку атомного ядра

1.Уважно прочитайте текст завдання.

2. Запишіть умову задачі.

3. Знайдіть кількість протонів Z і нейтронів N у ядрі атома.

4. Запишіть формулу енергії зв'язку атомного ядра.

5. Запишіть формулу дефекту маси.

5. Підставте числові значення фізичних величин з їх одиницями, проведіть розрахунок з одиницями.

6. Скористайтеся додатковою формулою для розрахунку питомої енергії зв'язку атомного ядра.

7. Підставте числові значення разом з одиницями виміру, проведіть розрахунок.

8. Проаналізуйте отримане значення.

3.2. Приклади задач

1. При переході електрона в атомі водню з четвертої стаціонарної орбіти на другу випромінюється фотон, що дає зелену лінію в спектрі водню. Визначити довжину хвилі цієї лінії, якщо при випромінюванні фотона атом втрачає енергію 2,53 еВ.

Д

Розв’язок:

Атом втрачає енергію випромінюваного фотона. ,

так як , значить . Звідки м

ано:

Е = 2,53 еВ = 4,05 ∙ 10^-19 Дж

h = 6 ∙ 10^-34 Дж ∙ с

с = 3 ∙ 10^-8 м/с

λ - ?

Відповідь:

2

Розв’язок:

Енергія одного такого кванта світла дорівнює . Число квантів . Відповідь:

. Скільки фотонів земного випромінювання з довжиною хвилі λ = 520 нм у вакуумі будуть мати енергію 10^-3 Дж?

Д ано:

λ = 520 нм

Е = 10^-3 Дж

n - ?

3. При переході електрона з деякої орбіти на другу атом водню випромінює світло з довжиною хвилі 4,34 ∙ 10^-7 м. Знайти номер невідомої орбіти.

Д

Розв’язок:

Використовуючи формулу для визначення довжини хвилі, що випромінює атом водню при переході з однієї орбіти на іншу:

, де R – стала Рідберга.

ано:

λ = 4,34 ∙ 10^-7 м

n = 2

n_к - ?

Звідки

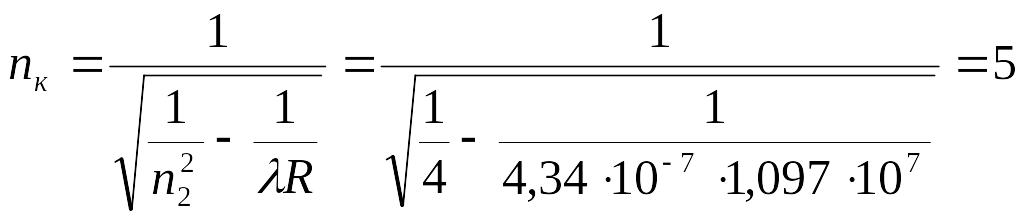
Відповідь: n = 5

4. Обчисліть енергію зв’язку ядра атома дейтерію.

Д ано: Розв’язок:

а.о.м. Енергія зв’язку ядра дорівнює ,де

= 1,00866 а.о.м. - різниця суми маси вільних частинок,

= 2,014110 а.о.м. які входять до складу ядра, та маси ядра; с

= 0,00055 а.о.м. – швидкість світла в вакуумі. Для

- ? - ? знаходження маси ядра дейтерію треба від маси атому

дейтерію відняти масу електрона, який знаходиться на

його оболонці:

;

.

Але 1 а.о.м. = , тому , а шукана енергія:

, або .

Відповідь: = 2,23 МеВ.

5

Розв’язок:

Радіоактивний розпад урану можна записати так:

, де α – частинка, β – частинка.

. Скільки відбувається α – і β – розпадів при радіоактивному розпаді , якщо він перетворюється в .

Д ано:

Застосовуючи закон збереження зарядових чисел, можна записати:

92 = 82 + х ∙ 2 – у ∙ 1 (1) , де х – число, α – розпадів,

у – число, β – розпадів.

Застосовуючи закон збереження масових чисел, можна записати:

238 = 198 + х ∙ 4 (2)

Розв’язуючи рівняння (1) і (2) як систему, отримаємо х = 10 і у = 10, тобто відбувається 10 α – розпадів і 10 – β – розпадів.

Відповідь: х = 10; у = 10.