
- •Методичні вказівки для практичних занять дисципліна «фізика»
- •Розділ 1 Механіка Практичне заняття № 1 Тема: Кінематика і динаміка матеріальної точки
- •1. Короткі теоретичні відомості
- •2. Алгоритм розв’язування задач. Приклади задач
- •2.1. Алгоритм розв’язування задач з кінематики матеріальної точки
- •2.2. Алгоритм розв’язування задач з динаміки матеріальної точки
- •2.3. Приклади задач
- •1. Рівномірний прямолінійний рух.
- •Розв’язок:
- •2. Рівнозмінний прямолінійний рух.
- •Розв’язок:
- •Рухався рівномірно зі швидкістю 30 м/с. Третю частину шляху він гальмував.
- •Знайдемо прискорення при гальмуванні; використовуючи Знайдемо весь шлях:
- •3. Вільне падіння тіл
- •Розв'язок:
- •4. Рух тіла під дією кількох сил
- •Розв'язок:
- •Розв'язок:
- •3. Самостійне розв’язування задач студентами
- •3.1. Якісні задачі
- •3.2. Розрахункові задачі
- •3.3. Тренувальний тест з «Кінематики»
- •3.4. Тренувальний тест з «Динаміки»
- •5. Підведення підсумків Питання для самоконтролю :
- •2. Алгоритм розв’язування задач. Приклади розв’язування задач
- •2.1. Закон збереження імпульсу
- •2.2. Закон збереження енергії
- •2.3. Приклади задач
- •Розв'язок:
- •Розв’язок:
- •Розв’язок:
- •Розв’язок:
- •Розв’язок:
- •3. Самостійне розв’язування задач студентами.
- •3.1. Якісні задачі
- •3.2. Розрахункові задачі
- •3.3. Тренувальний тест
- •5. Підведення підсумків Питання для самоконтролю
- •2. Алгоритм розв’язування задач. Приклади задач
- •2.1. Гази
- •2.2. Насичена пара. Вологість
- •2.3. Теплове розширення твердих і рідких тіл
- •Згідно рівняння Менделєєва - Клапейрона
- •Використовуючи рівняння стану ідеального газу
- •Розв’язок:
- •Розв’язок:
- •(Закон Шарля)
- •Р озв'язок
- •Розв’язок:
- •Розв’язок:
- •3. Самостійне розв’язування задач студентами
- •3.1.Якісні задачі
- •3.2. Розрахункові задачі
- •3.3. Тренувальний тест
- •5. Підведення підсумків Питання для самоконтролю:
- •3. Алгоритм розв’язування задач. Приклади задач.
- •3.2. Приклади задач
- •Розв’язок: Так як процес ізобарний, та за законом Гей-Люссака
- •Розв’язок:
- •Розв’язок:
- •Розв’язок: Представимо, що втрати енергії не присутні. Тоді
- •Розв’язок:
- •4. Самостійне розв’язування задач студентами
- •4.1. Якісні задачі
- •4.2. Розрахункові задачі
- •4.3. Тренувальний тест
- •5. Підведення підсумків Питання для самоконтролю
- •2. Алгоритм розв’язування задач. Приклади задач
- •2.1. Алгоритм розв’язування задач з теми «Електростатика»
- •2.2. Приклади задач
- •3. Самостійне розв’язування задач студентами
- •3.1. Якісні задачі
- •3.2. Розрахункові задачі.
- •3.3. Самостійна робота студентів.
- •4. Підведення підсумків Питання для самоперевірки:
- •2.2. Завдання про силову дію магнітного поля на заряджені частинки
- •2.3. Приклади задач
- •Розв’язок
- •Розв’язок:
- •3. Самостійне розв’язування задач студентами
- •3.1. Якісні задачі
- •3.2. Розрахункові задачі
- •3.3. Тренувальний тест
- •4. Підведення підсумків Питання для самоперевірки:
- •2.2. Приклади задач
- •Розв’язання:
- •Розв’язання:
- •3.2. Розрахункові задачі
- •3.3. Тренувальний тест
- •1. Короткі теоретичні відомості
- •2. Алгоритм розв’язування задач. Приклади задач
- •2.1. Алгоритм рішення задач на розрахунок коливального руху.
- •Рівняння гармонічних коливань має вигляд
- •Розв’язок:
- •Розв’язок:
- •Розв’язок:
- •Використовуючи формулу Томсона та ємності конденсатора ,
- •Розв’язок:
- •Розв’язок:
- •Розв’язок:
- •Розв’язок:
- •14. Яку ємність повинен мати конденсатор для того, щоб складений з цього конденсатора і котушки індуктивністю 10 мГн коливальний контур радіоприймача, був настроєний на хвилю 1000 м?
- •3. Самостійне розв’язування задач студентами.
- •3.1. Якісні задачі
- •3.2. Розрахункові задачі
- •3.3. Тренувальний тест
- •4. Підведення підсумків. Питання для самоконтролю
- •1. Короткі теоретичні відомості
- •2. Алгоритм розв’язування задач. Приклади задач.
- •2.1. Задачі на хвильові властивості світла
- •2.2. Приклади задач
- •3. Самостійне розв’язування задач студентами
- •3.1. Якісні задачі
- •3.2. Розрахункові задачі
- •3.3. Тренувальний тест
- •4. Підведення підсумків Питання для самоперевірки:
- •2. Алгоритм розв’язування задач. Приклади задач
- •2.1. Алгоритм розв’язування задач на фотоефект
- •2.2. Приклади задач
- •Розв’язок:
- •Розв’язок:
- •Розв'язок:
- •3. Самостійне розв’язування задач студентами
- •3.1. Якісні задачі
- •3.2. Розрахункові задачі
- •3.3. Тренувальний тест
- •3. Алгоритм розв’язування задач. Приклади задач
- •3.1. Алгоритм розв’язування задач на знаходження енергії зв’язку атомного ядра
- •3.2. Приклади задач
- •Розв’язок:
- •Розв’язок:
- •Розв’язок:
- •Розв’язок:
- •Розв’язок:
- •Розв’язок:
- •4. Самостійне розв’язування задач студентами
- •4.1. Якісні задачі
- •4.2. Розрахункові задачі
- •4.3. Тренувальний тест
- •5. Підведення підсумків Питання для самоконтролю:
- •Література:
- •Література:
2.3. Приклади задач
1. Рівномірний прямолінійний рух.
Дві
матеріальні точки рухаються вздовж
вісі абсцис рівномірно зі швидкістю
![]() та
та
![]() .
В початковий момент перша точка
знаходилась ліворуч від початку координат
на відстані 21 м, друга праворуч на
відстані 7 м. Через який час перша точка
дожене другу? Де це проходитиме. Намалюйте
графік руху.
.
В початковий момент перша точка
знаходилась ліворуч від початку координат
на відстані 21 м, друга праворуч на
відстані 7 м. Через який час перша точка
дожене другу? Де це проходитиме. Намалюйте
графік руху.
Д Знайдемо
координату зустрічі (покладемо

Розв’язок:
![]() -
рівняння рівномірного руху.
-
рівняння рівномірного руху.![]() -
рівняння руху першої точки.
-
рівняння руху першої точки.![]() -
рівняння руху другої точки. Знайдемо
час, коли вони зустрінуться. Тоді буде
виконуватись умова:
-
рівняння руху другої точки. Знайдемо
час, коли вони зустрінуться. Тоді буде
виконуватись умова: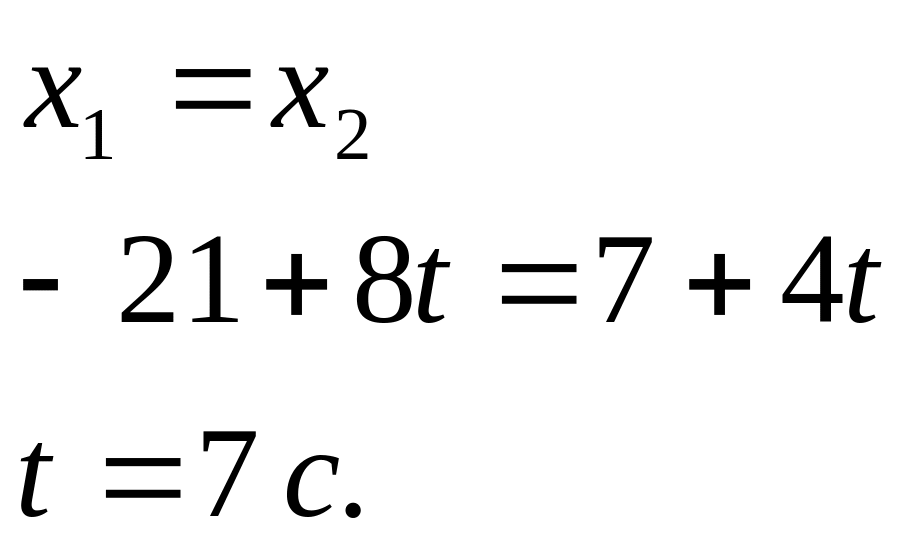
![]() в довільне рівняння руху)
в довільне рівняння руху)
![]()
![]()
![]()
![]()

![]()

Відповідь:
![]()
2. Рівнозмінний прямолінійний рух.
Мотоцикліст почав рухатись. На протязі 20 с рухався з прискоренням 1,5 м/с2, тоді 2 хвилини рухався рівномірно, а потім рівномірно гальмував на протязі 15 с і зупинився. Знайти максимальну швидкість, прискорення при гальмуванні та шлях.
Д
Розіб’ємо
шлях на 3 частини. Спочатку рух був
рівноприскореним
Другу частину
шляху мотоцикліст
Розв’язок:
![]()
![]()
![]()
Рухався рівномірно зі швидкістю 30 м/с. Третю частину шляху він гальмував.
 ано:
ано:


Знайдемо прискорення при гальмуванні; використовуючи Знайдемо весь шлях:
![]()
![]()
![]() .
.
![]()
Відповідь:
![]()
3. Вільне падіння тіл
Тіло, що падає без початкової швидкості, за останні 2 с пройшло відстань 8 = 40 м. Який час і тривало падіння та з якої висоти падало тіло?
Розв'язок:
![]()
![]()
![]() дістаємо:
дістаємо:
![]() звідки обчислюємо
звідки обчислюємо
![]() .
Підставляючи знайдений вираз для у
формулу, отримуємо:
.
Підставляючи знайдений вираз для у
формулу, отримуємо:
Використовуючи подані в умові числові дані, дістаємо: t = 3 с, Н = 45 м.
Час падіння можна обчислити й простіше, якщо скористатися тим, що середня швидкість у разі рівноприскореного руху дорівнює середньому арифметичному початкової та кінцевої швидкостей. Останню ділянку довжиною s тіло проходить за час, тому середня швидкість на цій ділянці —
![]() З
іншого боку, початкова швидкість на цій
ділянці дорівнює υ0
= g(t – τ), а кінцева швидкість при цьому
дорівнює υ = gt, тому
З
іншого боку, початкова швидкість на цій
ділянці дорівнює υ0
= g(t – τ), а кінцева швидкість при цьому
дорівнює υ = gt, тому
Отже,
![]() .
Звідси дістаємо:
.
Звідси дістаємо:
![]()
4. Рух тіла під дією кількох сил
1. Собача запряжка починає тягти санки масою 100 кг, що стоять на снігові, з постійною силою 150 Н. За який проміжок часу санки проїдуть перші 200 м шляху? Уважайте, що коефіцієнт тертя ковзання полоззя об сніг дорівнює 0,05.
Розв'язок:
Щоб обчислити час руху санок, необхідно знати прискорення, з яким рухаються санки, і початкову швидкість. Оскільки санки рушають з місця, то їхня початкова швидкість дорівнює нулю. Прискорення обчислимо, скориставшись другим законом Ньютона.
На санки діють чотири сили: сила тяжіння тg, сила реакції опори N, сила тяги собак FТ і сила тертя ковзання Fтерт.ковз.
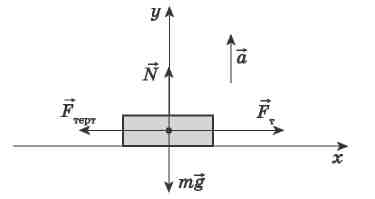
Запишемо другий закон Ньютона:
![]()
Спроектуємо рівняння на осі координат і запишемо вираз для сили тертя:
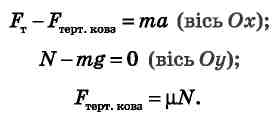
Ми отримали систему трьох рівнянь з трьома невідомими. Розв'язавши цю систему, ми й дістанемо прискорення:
![]()
Підставивши отриманий вираз у перше рівняння, дістаємо:
![]()
![]()
Для обчислення часу руху скористаємося рівнянням проекції переміщення для рівноприскореного руху:
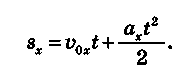
У нашому випадку:
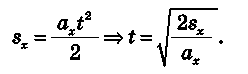
Підставляючи сюди значення прискорення, дістаємо:

Перевіряємо одиниці величин:
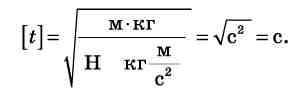
Виконуємо обчислення:
![]()
Відповідь: санки проїдуть перші 200 м за 20 с
2. Автомобіль масою 4 т рухається нагору, уповільнюючи свій рух. Обчисліть силу тяги, якщо ухил становить 0,02, а коефіцієнт опору руху дорівнює 0,04. Прискорення автомобіля постійне й дорівнює 0,15 м/с2.
