4. Підведення підсумків. Питання для самоконтролю
1. Які коливання називаються гармонічними?
2. Дайте означення основних величин, що характеризують гармонічні коливання.
3. Які коливання називаються вимушеними?
4. В чому заключається явище резонансу?
5. Що називають довжиною хвилі?
6. Яка хвиля називається поперечною та поздовжньою?
7. Які коливання називаються електромагнітними?
8. При яких умовах в коливальному контурі виникають електромагнітні
коливання?
9. Чим відрізняються вимушені електромагнітні коливання від вільних?
10. Які фізичні поняття та величина використовують для опису електромагнітних коливань?
11. Який вигляд мають рівняння, які описують коливальні процеси в контурі?
Література:
1. Гончаренко С.У. Фізика: підручник для загальноосвітніх шкіл. 11 кл.- К.: Освіта, 2002, с. 27 – 59.
Розділ 5 Оптика
Практичне заняття № 9
Тема: Хвильова оптика
Мета: навчити визначати максимуми і мінімуми інтерференції світла, різницю ходу між когерентними хвилями, довжину хвилі за формулою дифракційної решітки та практично застосовувати явище поляризації світла.
Знати: умови максимуму та мінімуму інтерференції світла, формулу дифракційної решітки.
Вміти: визначати максимуми і мінімуми інтерференції світла, довжину хвилі за формулою дифракційної решітки та практично застосовувати явище поляризації світла.
План
1. Короткі теоретичні відомості.
2. Алгоритм розв’язування задач. Приклади задач.
3. Самостійне розв’язування задач студентами.
4. Підведення підсумків.
1. Короткі теоретичні відомості
Оптична різниця ходу двох променів, утворених поділом фронту хвилі при проходженні через дві щілини в непрозорій ширмі або поділом амплітуди хвилі при відбитті від двох поверхонь плівки,
.
Умова інтерференційного максимуму:
де
m
= 0,
1,
2,
3,
… .
Умова інтерференційного мінімуму:
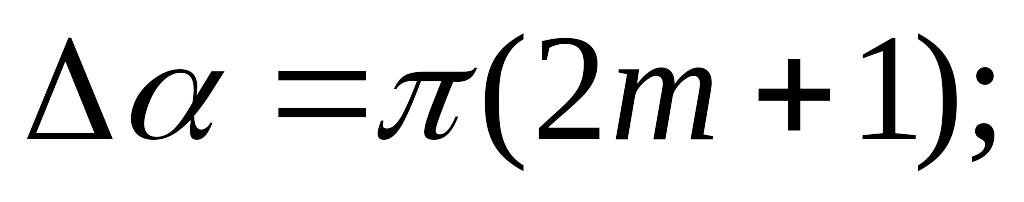
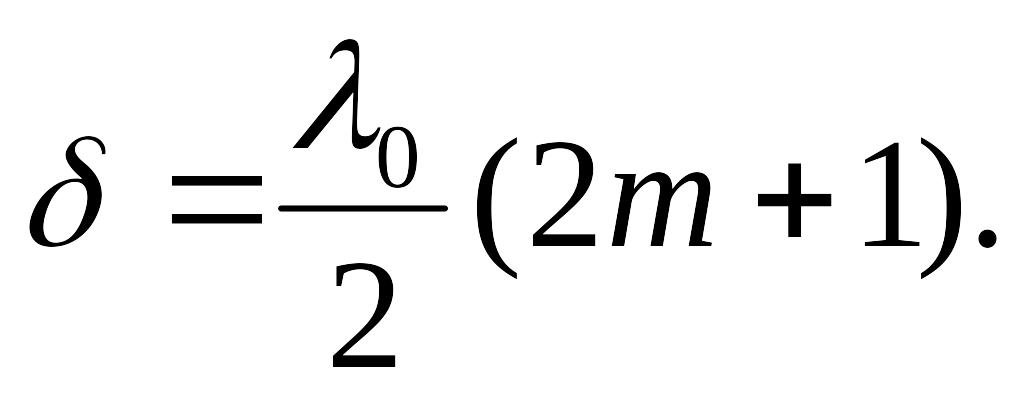
Дифракція світла. Умова головного максимуму:
де d – період решітки, φ – кут дифракції, k = 0, 1, 2, … – порядок максимуму.
2. Алгоритм розв’язування задач. Приклади задач.
2.1. Задачі на хвильові властивості світла
1. Зрозуміти запропоновану задачу (побачити фізичну модель).
2. Аналіз (побудувати математичну модель явища):
1. Встановити хвильове явище (інтерференція, дифракція, поляризація).
2. Зробити креслення, якщо це необхідно для розв’язку задачі
3. Записати формулу максимуму або мінімуму інтерференції світла, або формулу для дифракційної решітки.
4. Скласти допоміжні рівняння, що зв'язують фізичні величини, використовувані в задачі.
3. Отриману систему рівнянь вирішити відносно шуканої величини.
4. Рішення перевірити і оцінити критично
2.2. Приклади задач
1. В де яку точку простору приходять когерентні промені з геометричною різницею ходу l = 1,2 мкм, довжина хвилі λ яких в вакуумі 600 км. Визначити, що відбувається в цієї точці внаслідок інтерференції, коли промені проходить в повітрі, воді, скипидарі.
Д ано: Розв’язок:
n1
= 1 Оптична
різниця ходу в середовищах:
;
;
n = 1,33. Умовами інтерференційного максимуму є рівність оптичної
n3 = 1,5 різниці хода цілому числу довжини хвиль. Таким чином:
m
ax,
min - ?
; -
max
-
min
-
max
Відповідь: в першому і третьому випадку відбувається інтерференція max, а в другому – інтерференція – min.
2. На дифракційну решітку падає пучок світла від розрядної трубки, наповненої гелієм. На яку лінію в спектрі третього порядку накладається червона лінія гелію (λ1 = 6,7 ∙ 10-5 см) спектра другого порядку?
Д ано: Розв’язок:
k = 2 Для того щоб відбулося накладення спектрів, необхідно, щоб
k = 3 співпадали кути накладених променів:
;
-
? Таким чином,
.
Звідки
(см).
Відповідь: = 44,6 мкм
3. При спостереженні через дифракційну решітку червоний край спектру можна побачити на відстані 3,5 см від середини щілини в екрані. Відстань від дифракційної решітки до екрану – 50 см, період решітки – 1 мкм. Визначить довжину хвилі червоного світла.
Д ано: Розв’язок:
d
= 1 мкм Запишемо умову першого
максимуму:
. Так як кут
L
= 0,5 м дуже малий, то вірна слідуючи
рівність:
.
l
= 0,35 мм Тоді для визначення довжини
хвилі отримуємо вираз:
-
?
Відповідь: 0,7мкм