3.2. Розрахункові задачі

1. В провіднику довжиною активної частини 10 см. Сила струму дорівнює 45 А. Він знаходиться в однорідному магнітному полі з індукцією 35 мТл. Знайти здійснену роботу, якщо провідник змінився на 20 см перпендикулярно до ліній індукції.

2. Електрон рухається в магнітному полі з індукцією . Знайти період обертання електрона.

3. Знайти кінетичну енергію протона, який рухається по колу радіусом 6 см в магнітному полю, індукція якого дорівнює 0,1 Тл. Відповідь виразити в електронвольтах.

4. Магнітна індукція в бруску металу дорівнює 0,75 Тл, а магнітна індукція зовнішнього поля 37,5 мТл. Визначити магнітну проникність металу.

3.3. Тренувальний тест

1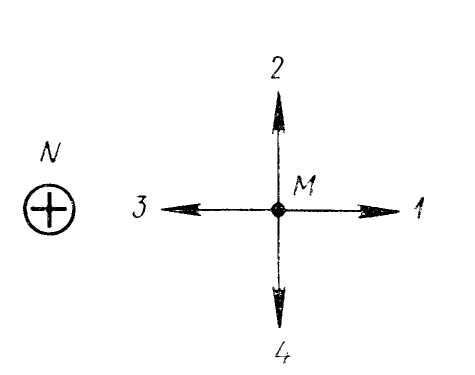 . На рисунку зображено переріз провідника зі струмом в точці N, електричний струм входить перпендикулярно в плоскість рисунка. Вектор В індукції магнітного поля струму в точці М має напрямок...

А) 1. Б) 2. В) 3. Г) 4.

2. Розташування ліній індукції магнітного поля навколо прямолінійного провідника зі струмом, перпендикулярного плоскості рисунка має вигляд...

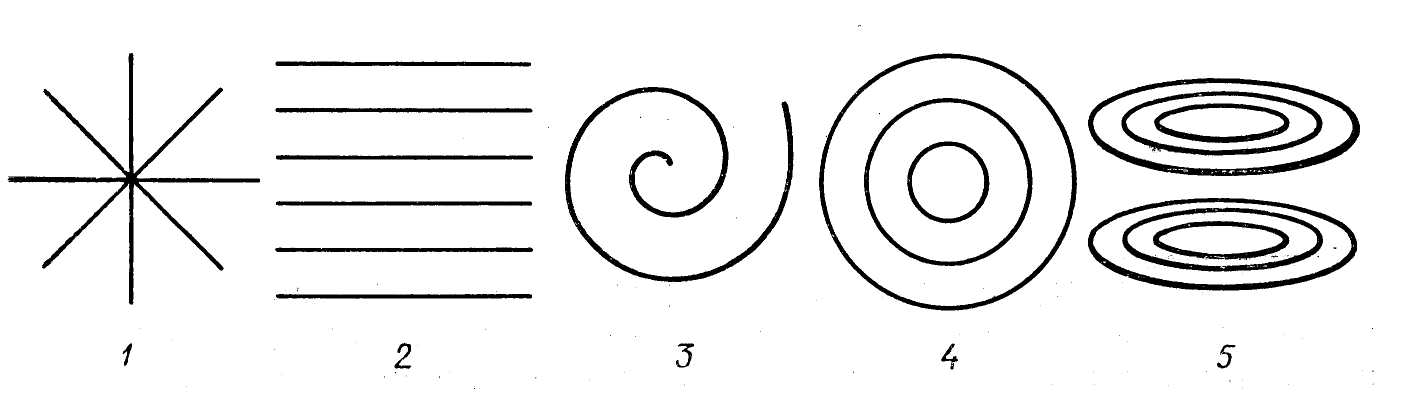
А) 1. Б) 2. В) 3. Г) 4. Д) 5.

3. Вектор сили F, який діє зі сторони магнітного поля на рухомий позитивний електричний заряд, при напрямку вектора υ швидкості заряду, який співпадає з напрямом вектора В індукції магнітного поля має напрямок...

А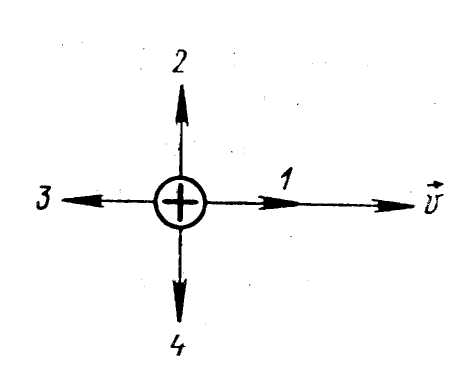 ) Співпадає з напрямом вектора В. Б) Протилежно вектору В. В) Перпендикулярно вектору В. Г) Може мати любий напрямок. Д) F=0.

4. На рисунку указано напрямок вектора швидкості руху позитивного заряду. Вектор сили, діючий зі сторони магнітного поля на цей заряд, якщо вектор індукції входить перпендикулярно в плоскість рисунка має напрямок....

А) 1. Б.) 2. В) 3. Г) 4.

5. Вектор швидкості заряду перпендикулярний вектору індукції магнітного поля. Сила, діюча на електричний заряд з боку магнітного поля при збільшені швидкості заряду в 2 рази і збільшені індукції магнітного поля в 2 рази...

А) ... збільшиться в 4 рази. Б) ... збільшиться в 2 рази. В) ... не зміниться. Г) ... зменшиться в 2 рази. Д) ... зменшиться в 4 рази.

Таблиця відповідей

Завдання	1	2	3	4	5
Відповідь	В	Г	Б	Б	А

4. Підведення підсумків Питання для самоперевірки:

1 Перерахуйте основні властивості магнітного поля.

2 Як визначити модуль вектора магнітної індукції?

3 Вкажіть способи визначення напрямку вектора магнітної індукції.

4 Що називають лініями магнітної індукції?

5 Які поля називають вихровими?

6 Чому дорівнює модуль сили Ампера? Як визначити її напрямок?

7 Чому дорівнює модуль сили Лоренца?

8 У чому сутність гіпотези Ампера?

9 Які тіла називають феромагнетиками?

Література:

1. Гончаренко С.У. Фізика: Пробний навчальний посібник для шкіл ІІІ ступеня, гімназії і класів гуманітарного профілю. 10 кл.- К.: Освіта, 1995, с. 207-230.

Практичне заняття № 7

Тема: Електромагнітна індукція

Мета: визначати електрорушійну силу електромагнітної індукції, індуктивність та енергію магнітного поля, ідентифікувати зв’язок між електричними і магнітним полем, застосовувати закон електромагнітної індукції та закон Ленца; визначати характеристики і закони магнітного кола.

План

1. Короткі теоретичні відомості.

2. Алгоритм розв’язування задач. Приклади задач.

3. Самостійне розв’язування задач студентами.

4. Підведення підсумків.

1. Короткі теоретичні відомості

• ЕРС індукції в контурі

E _i ,

де Ф – створюваний струмом в контурі магнітний потік через поверхню, охоплену контуром.

• ЕРС самоіндукції E _c .

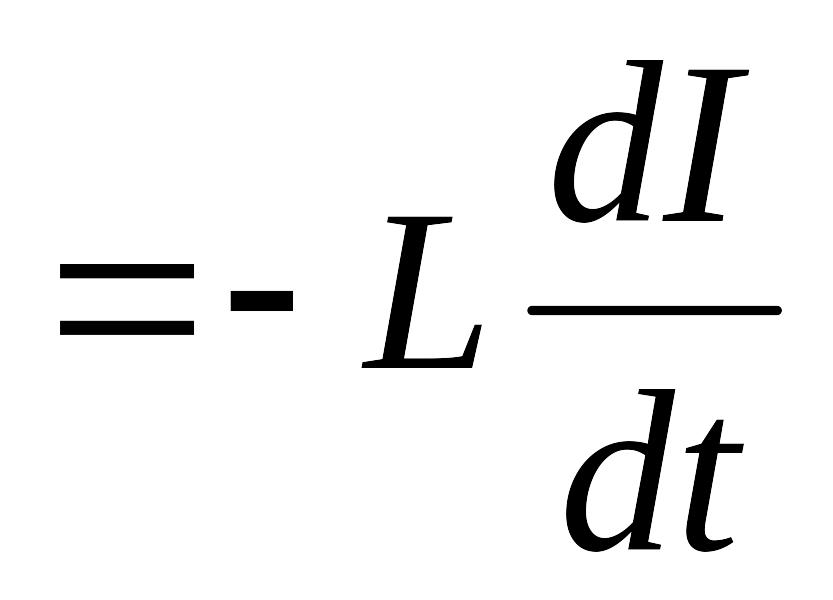• Енергія магнітного поля провідника .

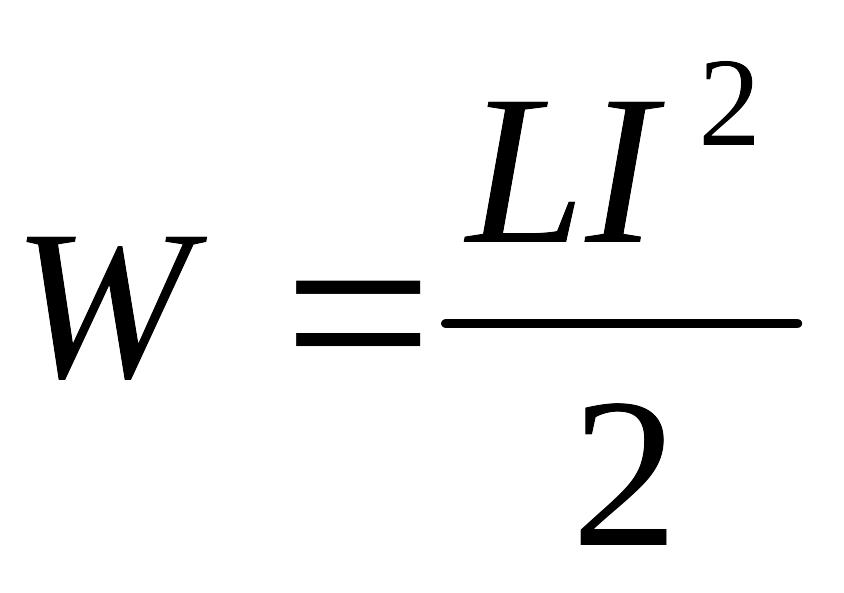• Густина енергії магнітного поля .

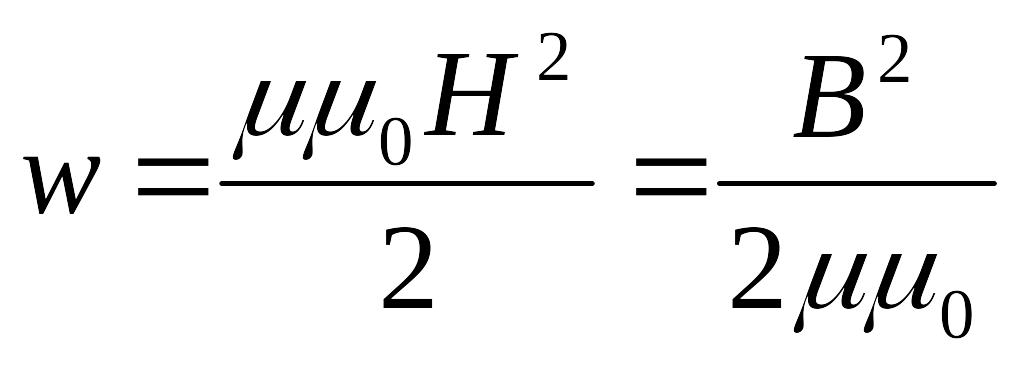2. Алгоритм розв’язування задач. Приклади задач

2.1. Закон електромагнітної індукції.

1. Зрозуміти запропоновану задачу (побачити фізичну модель).

2. Аналіз (побудувати математичну модель явища):

1. Встановити причини зміни магнітного потоку, пов'язаного з контуром, і визначити яка з величин В, S або, що входять у вираз для Ф, змінюється з часом.

2. Записати формулу закону електромагнітної індукції.

3. Вираз для Ф представити в розгорнутому вигляді (ΔФ) і підставити у вихідну формулу закону електромагнітної індукції.

4. Записати математично всі допоміжні умови.

3. Отриману систему рівнянь вирішити відносно шуканої величини.

4. Рішення перевірити і оцінити критично.