2.2. Завдання про силову дію магнітного поля на заряджені частинки

1. Зрозуміти запропоновану задачу (побачити фізичну модель).

2. Аналіз (побудувати математичну модель явища):

1. Потрібно зробити креслення, вказати на ньому силові лінії магнітного та електричного полів, проставити вектор початкової швидкості частинки і відзначити знак її заряду.

2. Зобразити сили, що діють на заряджену частинку.

3. Визначити вид траєкторії частинки.

4. Розкласти сили, що діють на заряджену частинку, уздовж напрямку магнітного поля і за напрямком, йому перпендикулярному.

5. Скласти основне рівняння динаміки матеріальної точки по кожному з напрямків розкладання сил.

6. Виходячи з фізичної природи сил, висловити сили через величини, від яких вони залежать.

3. Вирішити отриману систему рівнянь щодо невідомої величини.

4. Рішення перевірити і оцінити критично.

2.3. Приклади задач

1. По горизонтальному провіднику довжиною 20 см та масою 4 г протікає струм силою 10 А. Знайти індукцію магнітного поля в яке треба помістити провідник, щоб він знаходився у стані рівноваги.

Д

Розв’язок

Провідник буде в стані рівноваги якщо буде виконуватись умова рівноваги.

ано:

l = 20 см = 0,2 м

І

; α = 90^о sin α = 1,, тоді , звідси

Відповідь:

= 10 А

m = 4 г = 4·10^-3 кг

В – ?

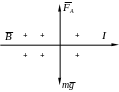
2. Протон в магнітному полі з індукцією 0,01 Тл описав коло радіуса 10 см. Знайти швидкість протона на період його обертання.

Д

Розв’язок:

На протон, який рухається в магнітному полі діє сила Лоренца, яка визначається по формулі

; α = 90^о sin α = 1.

Ця сила спрямована по радіусу до центру і надає протону доцентрове прискорення

ано:

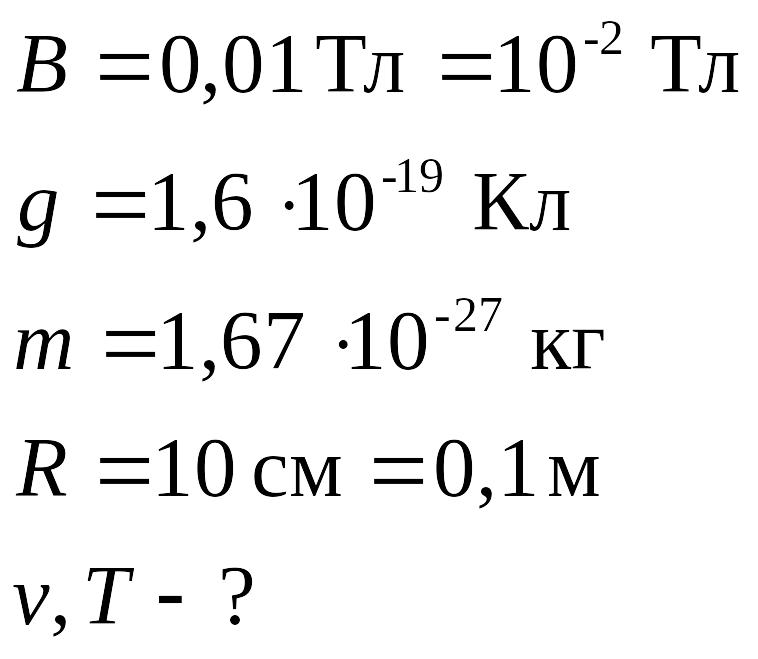
Тоді: ; ; ;

Період обертання протона

Відповідь: ;

3. Електрон, прискорений різницею потенціалів U = 1000 В, влітає в однорідне магнітне поле з індукцією перпендикулярно до лінії індукції. Визначити радіус кривизни траєкторії електрона і період його обертання по колу.

Д ано: Розв’язок:

U = 1000 B Відповідно закону збереження енергії робота сил поля дорівнює

зміні кінетичної енергії електрона , звідки .

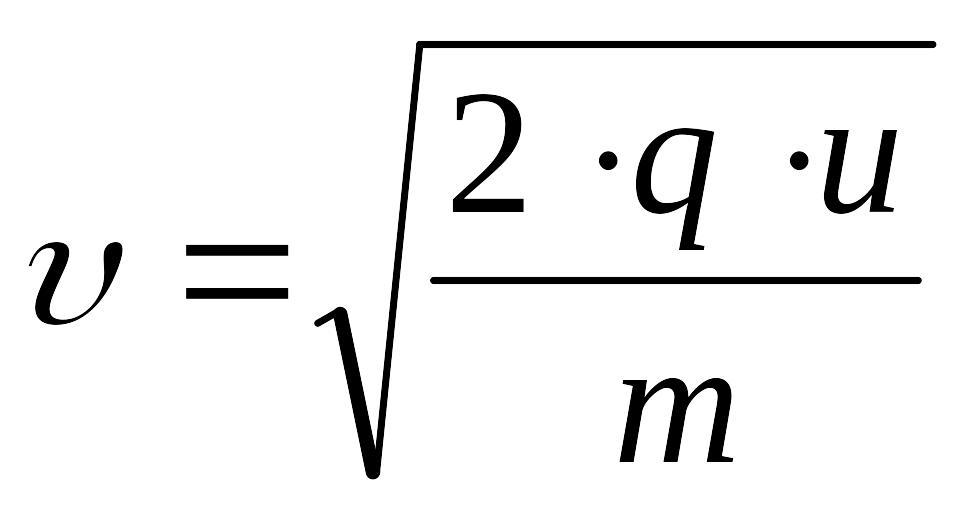Сила Лоренца, діюча на електрон в магнітному полі є доцентровою

силою, тобто так як

R - ?, T - ? отримуємо:

, звідки .

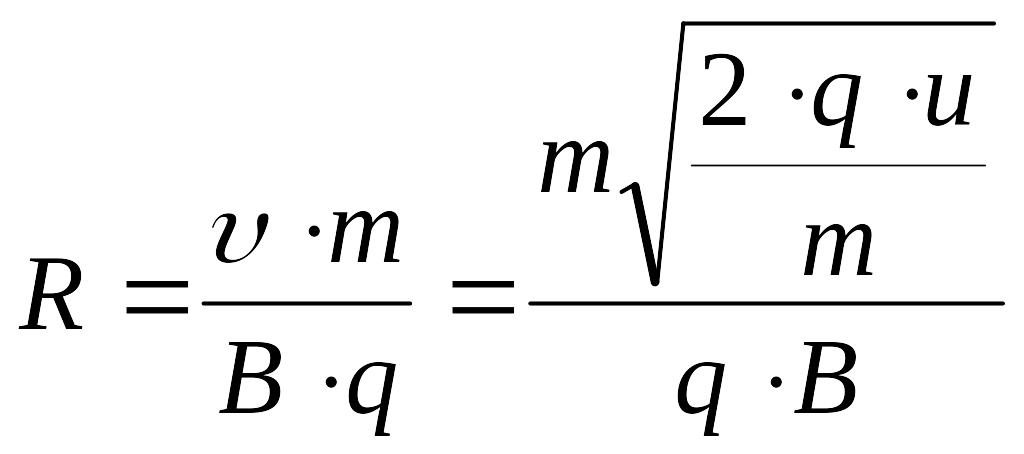Знаючи радіус кола, його довжину , а також швидкість електрона, знайдемо період обертання: , .

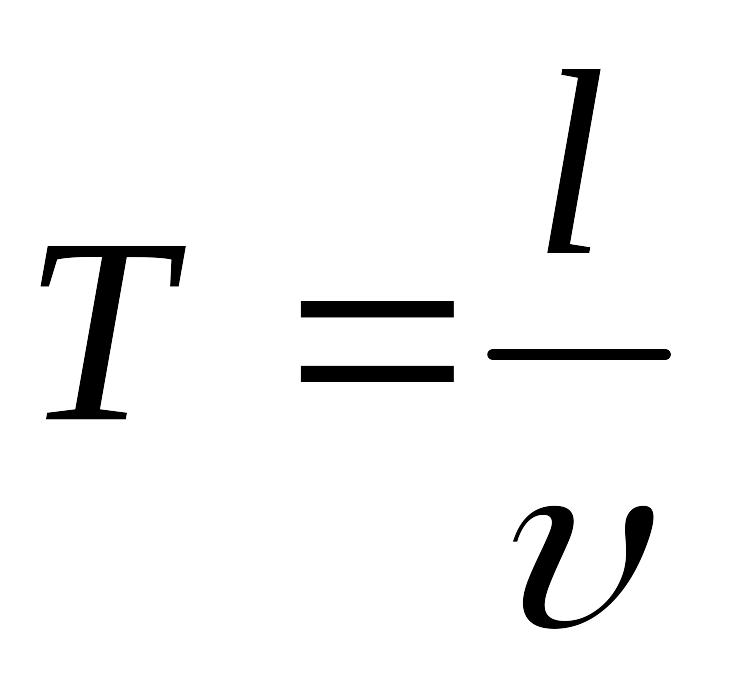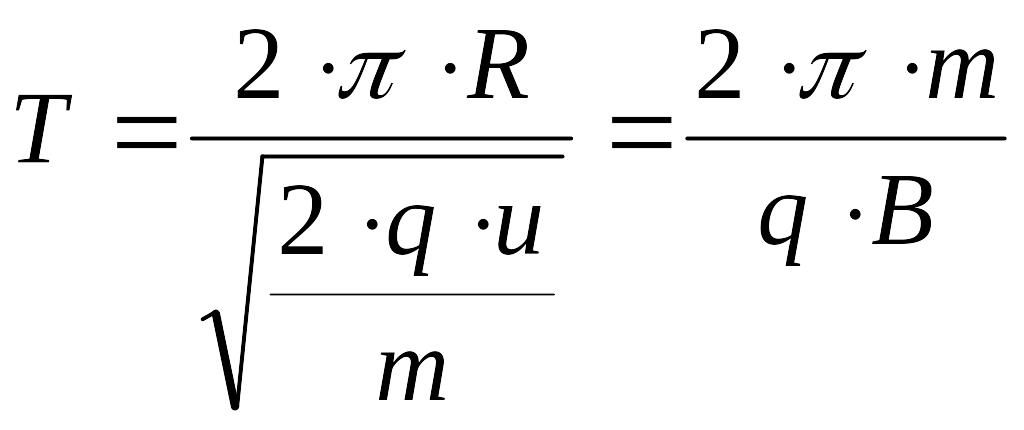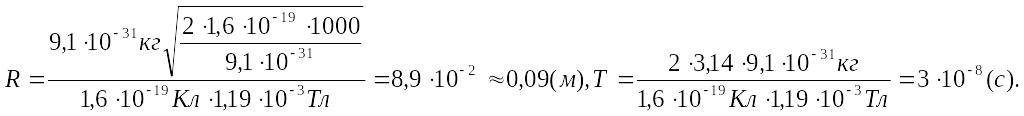Відповідь: R = 0,1 м, Т = .

3. Самостійне розв’язування задач студентами

3.1. Якісні задачі

1. Якщо кілька разів піднести до годинника сильний магніт, то показання годинника будуть невірними. (Іноді через декілька днів годинник відновлює правильний хід). Як можна пояснити це явище?

2. Як побудувати сильний електромагніт, якщо поставлена умова, щоб струм у ньому був відносно слабким?

3. У якому місці Землі магнітна стрілка обома кінцями вказує на південь?

4. Чому сталеві віконні ґрати з часом намагнічуються?

5. При підготовці польотів на Північний полюс багато уваги приділялося забезпеченню орієнтації літака поблизу полюса з-за того, що там звичайні магнітні компаси працюють погано і є практично непридатними. Чому?