Д

Розв’язок:

Розглянемо кисень, як ідеальний газ. Тоді ізотермічний процес описується рівнянням pV = cоnst (закон Бойля-Маріотта). Кисень розширяється в порожнечу (р₂ = 0) тобто відбувається збільшення об’му. Отримаємо , звідки

(Па)

ано:

V₁ = 2,8 · 10^-3 м³

p₁ = 2 · 10⁷ Па

V₂ = 5 · 10^-2 м³

p₂ = 0

T = const

p ₃ - ?

Відповідь: 1,06 · 10⁶ Па.

4

Розв’язок:

Об’єм кабіни не змінюється. Якщо розглядати повітря як ідеальний газ, процес відбувається ізохорний, і описується рівнянням

(Закон Шарля)

Після підстановки даних з умови задачі отримаємо

. Тиск в кабіні космічного корабля при температурі 290 К дорівнює 9,7 ∙ 10⁴ Па. Як зміниться тиск повітря при збільшенні температури на 8 К?

Д ано:

Т₁ = 290 К

р₁ = 9,7 ∙ 10⁴ Па

Т₂ = Т₁ + 8 К

р ₂ - ?, Δр - ?

, звідки (Па).

Зміна тиску Δр = р₂ – р₁ = 9,97 ∙ 10⁴ Па – 9,7 ∙ 10⁴ Па = 2,7 ∙ 10³ Па.

Відповідь: = 9,97∙ 10⁴ Па; Δр = 2,7 ∙ 10³ Па.

5. Побудуйте графіки процесу, що відбувається з ідеальним газом, у координатах VТ і рV. Маса газу постійна.

Р озв'язок

Перш ніж будувати графіки, потрібно з'ясувати, що собою представляє кожен етап замкнутого процесу, що відбувається з газом. (Скориставшись газовими законами, можна зробити висновок і дати характеристику зміни об'єму газу на кожному з етапів.) Етап 1-2 — це ізотермічне розширення (температура постійна, тиск зменшується), етап 2-3 — ізобарне охолодження (тиск постійний, температура зменшується), етап 3-1 — ізохорне нагрівання (тиск збільшується прямо пропорційно абсолютній температурі газу).

При побудові графіків у координатах VТ і рV слід враховувати, що ці графіки повинні бути замкнутими.

6

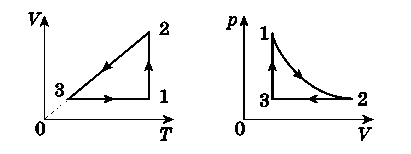
Розв’язок:

Поверхневий натяг визначається за формулою , де , а . Маса речовини визначається , де . Тоді . Звідси .

Відповідь: мм.

. В ювелірній техніці “зернь” на поверхню виробу напаюють дрібні золоті або срібні кульки. Якого діаметру d срібний дріт треба взяти, щоб при його плавленні від нього відривалися краплі діаметром D = 1 мм? Коефіцієнт поверхневого натягу розплавленого срібла , густина .

Д ано:

D = 1 мм = 10^-3м

.

d - ?

7

Розв’язок:

Висота підняття рідини в капілярі визначається

. В нашому випадку , тоді .

. У денці скляної посудини з’явилась тріщина. Якщо рівень ртуті в посудині перевищує h = 20 см, ртуть починає витікати через тріщину. Густина ртуті  = 13600 кг/м³, коефіцієнт поверхневого натягу  = 0,5 Н/м. Знайдіть ширину d тріщини.

Дано:

h = 20 см = 0,2 м

 = 13600 кг/м³

 = 0,5 Н/м

d - ?

Відповідь: мкм.

8. Об’єм скляної колби при 0 С дорівнює 400 см . Колбу заповнюють ртуттю та нагрівають до 100 С . При цьому з колби витікає 6,12 см . Визначити коефіцієнт об’ємного розширення ртуті.

Д ано : Розв’язок :

V =400 см Коефіцієнт об’ємного розширення ртуті можна знайти за

t=100 формулою . Справжнє розширення ртуті

V =6.12 см дорівнює сумі збільшення об’єму колби та уявного

розширення ртуті . Збільшення обєму

? скляної колби можна знайти за формулою коефіцієнта

об’ємного розширення, враховуючи, що .

Знаходимо збільшення об’єму скляної колби при нагріванні .

= =

Відповідь: =0,00018 .

9. Для підвищення швидкості руху потягів рейки укладаються без стиків. Знайти механічне напруження  в поперечному перерізі такої рейки, якщо її температура змінилася з моменту укладання на Т = 30 К. При якій зміні температури рейки почнуть розриватися? Модуль пружності Е = 220 ГПа, границя міцності коефіцієнт лінійного теплового розширення К.

Д ано : Розв’язок :

К Відповідно закону Гука, маємо , де . Тоді

Е= 220 ГПа .

К.

К

- ?

- ? Відповідь: МПа; К.