
- •1. Инженерлік графика нені зерттейді және оның негізгі мақсаттары
- •2. Монж әдісі ,Проекциялық жазықтықтар
- •3. Ортогональді проекциялау Сандық өлшеулері бар проекциялар
- •4. Октанттар. Екі проекциялық жазықтықтағы нүктенің ортогональді проекциясы
- •5. Позициялық және метрикалық есептер
- •4.1.1 Нүкте мен түзу сызықтың өзара орналасулары
- •4.1.2 Түзу сызықтардың өзара орналасулары
- •4.1.3 Екі жазықтықтың өзара орналасуы
- •4.1.4 Түзу мен жазықтықтың өзара орналасулары
- •4.2 Метрикалық есептер
- •4.2.1 Түзу сызықтың нақты шамасы мен жазықтыққа жасайтын бұрышы
- •7.Түзусызық. Түзусызықтың графикалық берілу әдісі. Проекция жазықтығына қатысты түзу сызықтың орналасуы
- •1. Параллель түзулер .
- •2. Қиылысатын түзулер.
- •12. Екі түзудің өзара орналасуы
- •13. Ортогональды проекцияларды түрлендірулердің әдістері
- •14 Ортогональды проекцияларды түрлендірулердің әдістері
- •14.Проекциялар жазықтығына препендикуляр өс бойынша айналдыру әдісі
- •15.Ортогональды проекцияларды түрлендірулердің әдістері
- •17. Нүкте мен түзудің өзара орналасуы
- •18. Түзу сызықты кесіндіні берілген қатынасқа бөлу
- •19. Орталық проекциялау
- •20. Нүкте үш проекция жазықтықтарының ортогональды жүйесінде
- •21. Ортогоналдық проекцияларды түрлендіру әдістері.Проекция жазықтықтығына параллел өсі бойынша айналдыру әдісі
- •21.Проекциялар жазықтығына параллель өс бойынша
- •23 Жазықтық. Жазықтықтың графикалық берілу әдістері
- •24 Проекция жазықтығына қатысты жазықтықтың әртүрлі орналасуы
- •25. Жазықтықтың ізі
- •26. Жазықтыққа перпендикуляр түзу сызық
- •27. Нүкте мен жазықтықтың өзара орналасуы
- •28. Түзу мен жазықтықтың өзара орналасулары
- •29. Екі жазықтықтың өзара орналасуы.
- •30. Түзудің іздері.
- •31. Жазықтыққа перпендикуляр туралы теорема
- •32. Параллель проекциялау əдісі
- •32 Паралель проекция.
- •33.Түзудің жазықтыққа қатысты орналасуы
- •34. Проекция жазықтығына байланысты жазықтықтың әр түрлі болып орналасуы
- •36. Жазықтықтардың негізгі әдістері
- •37.Көпжақтылар
- •38. Көпжақтылар мен жазықтықтардың қиылысуы.
- •39. Түзудің көпжақтылармен қиылысуы
- •40. Көпжақты беттердің өзара қиылысуы
14.Проекциялар жазықтығына препендикуляр өс бойынша айналдыру әдісі
Нүктелерді орын ауыстыру траекториясы проекциялар жазықтығына параллель. Траектория – шеңбердің доғасы, центрі проекциялар жазықтығына перпендикуляр өсте орналасқан. АВ (4.4. - сурет) жалпы жағдайдағы түзу кесіндісінің шынайы өлшемін анықтау үшін, В1 нүктесі арқылы өтетін горизонталь жазықтығына перпендикуляр айналдыру өсін аламыз. Кесіндіні фронталь проекциялар жазықтығына параллель болатындай етіп бұрамыз (кесіндінің гоизонталь проекциясы x өсіне параллель). Осыған байланысты А1 нүктесі А1*, m2 нүктесіне орналасады, ал В нүктесі өз күйін өзгертпейді. А2* нүктесі А нүктесі траекториясының фронталь проекцияларының қиылысында орналасқан (түзу сызық x өсіне параллель). В2 А2* алынған проекциясы кесіндінің өлшемін анықтайды.
|
|
4.4. - Сурет. Горизонталь проекциялар жазықтығына препендикуляр өс бойынша айналдыру әдісімен кесіндінің шынайы өлшемін анықтау |
|
15.Ортогональды проекцияларды түрлендірулердің әдістері
Егер түзу проекция жазықтықтарының біріне параллель болса, онда ортогональды проекцияларды түрлендірмей-ақ, тек қана перпендикулярдың проекциясын тапқан жеткілікті. Егер f түзуі фронталь, яғни f \\ П2 онда А нүктесінің А2 фронталь проекциясынан m түзуінің m2 фронталь проекциясына перпендикуляр жүргізуге болады. АК- кесіндісі жалпы жағдайдағы түзу болғандықтан, АК – кесіндісінің алынған проекциялары кесіндінің шынайы өлшемін бермейді.
|
|
4.2. - Сурет. Нүктеден фронталь түзуге дейінігі арақашықтық |
|
Келтірілген сызбалардың қойылуы, есепті шешу қиындығы гоометриялық объектілердің проекциялар жазықтығына қарағанда оналасуынан тәуелді болатындығын көрсетеді.
Осыған байланысты қолайсыз ортогональды проекциялар арқылы қойылған есептің шешімін табу үшін қолайлы проекцияларды қандай жолмен алуға болады деген сұрақ туындайды.
Жалпы жағдайдағы геометриялық фигураны жеке жағдайға ауыстыру проекциялаушы фигура мен проекциялар жазықтықтарының өзара орналасуын өзгерту арқылы жүзеге асыруға болады.
Ортогональды проекциялау 2 жолмен жүзеге асады:
1. Кеңістікте проекцияланушы фигураның орналасуы, проекциялар жазықтығына қарағанда жеке жағдайда болуы керек, сонымен қатар кеңістікте өз орналасу жағдайын өзгертпейді – жазық параллельді орналасу әдісі. 2. Проекциялар жазықтығын жаңа жағдайға ауыстыру, проекцияланушы фигура жеке жағдайда болады – проекциялар жазықтығын ауыстыру әдісі.
проекциялар жазықтығына параллель өс бойынша
айналдыру әдісі
Бұл әдісті өзара қиылысушы түзулердің бұрышын анықтайтын мысалда қарастырайық (4.5. - сурет). К нүктесінде қиылысатын а мен в қиылысушы түзулерінің екі проекциясын қарастырамыз. Осы түзулердің арасындағы бұрыштың шынайы өлшемін анықтау үшін, түзулерді проекциялар жазықтығына параллель болатындай етіп түрлендіру қажет. Горизонталь деңгейлік түзу бойымен айналдыру әдісін қолданамыз. Кез-келген a және b түзулерін қиып өтетін Ох өсіне параллель h2 горизонталін фронталь проекциясына жүргіземіз.
|
|
|
|
К1 нүктесінің қозғалыс траекториясы К1О1 түзуімен анықталған, О нүктесі шеңбердің центрі. Шеңбердің радиусын анықтау үшін КО кесіндісінің шынайы өлшемін үшбұрыш әдісімен табамыз. К1О1 түзуін |КО|=|О1К1*| болғанша созамыз. Егер түзулері П1 жазықтығына параллель жазықтықта жататын болса және горизонталь айналу өсі бойынша жүргізілген, онда К1* нүктесі К нүктесіне сәйкес келеді. П1 – ге параллель жазықтықта орналасқан К1* нүктесі мен А1, В1 нүктелері арқылы түзулер жүргіземіз. Осы екі түзудің арасындағы бұрыш а мен в арасындағы бұрышының φ бұрышының шынайы мәні болады

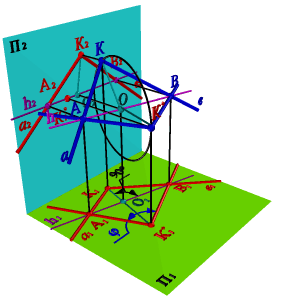
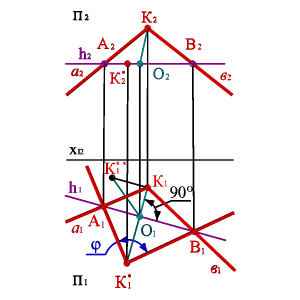 4.5.
– Сурет.
Горизонталь
проекциялар жазықтығына параллель
өс бойынша айналу арқылы қилысушы
түзулердің арасындағы бұрыштарды
анықтау
4.5.
– Сурет.
Горизонталь
проекциялар жазықтығына параллель
өс бойынша айналу арқылы қилысушы
түзулердің арасындағы бұрыштарды
анықтау