
- •1. Инженерлік графика нені зерттейді және оның негізгі мақсаттары
- •2. Монж әдісі ,Проекциялық жазықтықтар
- •3. Ортогональді проекциялау Сандық өлшеулері бар проекциялар
- •4. Октанттар. Екі проекциялық жазықтықтағы нүктенің ортогональді проекциясы
- •5. Позициялық және метрикалық есептер
- •4.1.1 Нүкте мен түзу сызықтың өзара орналасулары
- •4.1.2 Түзу сызықтардың өзара орналасулары
- •4.1.3 Екі жазықтықтың өзара орналасуы
- •4.1.4 Түзу мен жазықтықтың өзара орналасулары
- •4.2 Метрикалық есептер
- •4.2.1 Түзу сызықтың нақты шамасы мен жазықтыққа жасайтын бұрышы
- •7.Түзусызық. Түзусызықтың графикалық берілу әдісі. Проекция жазықтығына қатысты түзу сызықтың орналасуы
- •1. Параллель түзулер .
- •2. Қиылысатын түзулер.
- •12. Екі түзудің өзара орналасуы
- •13. Ортогональды проекцияларды түрлендірулердің әдістері
- •14 Ортогональды проекцияларды түрлендірулердің әдістері
- •14.Проекциялар жазықтығына препендикуляр өс бойынша айналдыру әдісі
- •15.Ортогональды проекцияларды түрлендірулердің әдістері
- •17. Нүкте мен түзудің өзара орналасуы
- •18. Түзу сызықты кесіндіні берілген қатынасқа бөлу
- •19. Орталық проекциялау
- •20. Нүкте үш проекция жазықтықтарының ортогональды жүйесінде
- •21. Ортогоналдық проекцияларды түрлендіру әдістері.Проекция жазықтықтығына параллел өсі бойынша айналдыру әдісі
- •21.Проекциялар жазықтығына параллель өс бойынша
- •23 Жазықтық. Жазықтықтың графикалық берілу әдістері
- •24 Проекция жазықтығына қатысты жазықтықтың әртүрлі орналасуы
- •25. Жазықтықтың ізі
- •26. Жазықтыққа перпендикуляр түзу сызық
- •27. Нүкте мен жазықтықтың өзара орналасуы
- •28. Түзу мен жазықтықтың өзара орналасулары
- •29. Екі жазықтықтың өзара орналасуы.
- •30. Түзудің іздері.
- •31. Жазықтыққа перпендикуляр туралы теорема
- •32. Параллель проекциялау əдісі
- •32 Паралель проекция.
- •33.Түзудің жазықтыққа қатысты орналасуы
- •34. Проекция жазықтығына байланысты жазықтықтың әр түрлі болып орналасуы
- •36. Жазықтықтардың негізгі әдістері
- •37.Көпжақтылар
- •38. Көпжақтылар мен жазықтықтардың қиылысуы.
- •39. Түзудің көпжақтылармен қиылысуы
- •40. Көпжақты беттердің өзара қиылысуы
1. Параллель түзулер .
Бір жазықтықта жататын және ортақ нүктелері жоқ екі түзу параллель түзулер деп аталады.
|
|
Параллель түзулердің кез-келген жазықтықтағы проекциялары параллель болады.
Параллель проекциялардың бұл қасиеті ортогональды проекциялар үшін де қолданылады, егер AB//CD онда A1B1//C1D1; A2B2//C2D2; A3B3//C3D3 (3.19 сурет).
Жазықтықтардың біріне параллель түзу ерекше жағдайды ұстанады. Мысалы, профиль түзудің фронталь және горизонталь проекциялары параллель, бірақ олардың өзара орналасуын анықтау үшін профиль проекциялар жазықтығында түзулердің проекцияларын салу қажет.(3.20. - сурет). Қарастырып отырған жағдайда кесінділердің П3 жазықтығындағы проекциялары қиылысады, демек шығатын қорытынды, олар параллель емес.
Бұл сұрақтың шешімін екі қатынасты салыстыру арқылы аламыз:
А2В2/ А1В1= С2Д2/ С1 Д1Þ АВ//СД
А2В2/ А1В1¹ С2Д2/ С1Д1Þ АВ//СД
|
|
2. Қиылысатын түзулер.
Бір жазықтықта жататын ортақ нүктелері бар екі түзу қилысушы түзулер деп аталады. Егер түзулер қиылысатын болса, онда олардың аттас проекцияларының қиылысу нүктелері бір байланыс сызығының бойында жатады. (3.21. - сурет).
|
||||
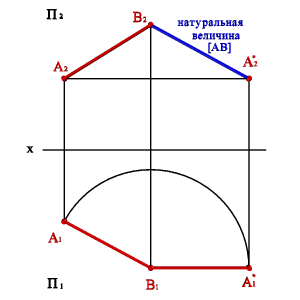
9. проекциялар жазықтығына препендикуляр өс бойынша айналдыру әдісі Нүктелерді орын ауыстыру траекториясы проекциялар жазықтығына параллель. Траектория – шеңбердің доғасы, центрі проекциялар жазықтығына перпендикуляр өсте орналасқан. АВ (4.4. - сурет) жалпы жағдайдағы түзу кесіндісінің шынайы өлшемін анықтау үшін, В1 нүктесі арқылы өтетін горизонталь жазықтығына перпендикуляр айналдыру өсін аламыз. Кесіндіні фронталь проекциялар жазықтығына параллель болатындай етіп бұрамыз (кесіндінің гоизонталь проекциясы x өсіне параллель). Осыған байланысты А1 нүктесі А1*, m2 нүктесіне орналасады, ал В нүктесі өз күйін өзгертпейді. А2* нүктесі А нүктесі траекториясының фронталь проекцияларының қиылысында орналасқан (түзу сызық x өсіне параллель). В2 А2* алынған проекциясы кесіндінің өлшемін анықтайды.
11. Проекция жазықтығын алмастыру тəсілі Проекция жазықтығын алмастыру тəсілінің маңызы – күрделі есептерді шешу үшін, көлденең П0 проекция жазықтығын бір жазықтықпен немесе екі жазықтықпен алмастыру арқылы есептің шешуін табуға болады. Егер геометриялық фигуралардың кескініне бірінші проекция жазықтығын параллель алсақ, онда екінші проекция жазықтығын сол кескінге перпендикуляр етіп орналастырамыз. Осы тəсілді пайдаланып, түзудің жəне жазықтықтың нақты шамасын, түзу мен жазықтықтың немесе екі жазықтықтың бұрыштық шамасын, нүкте мен жазықтықтың арақашықтығын жəне тағы басқа сол сияқты есептерді шешуге болады.
|
||||

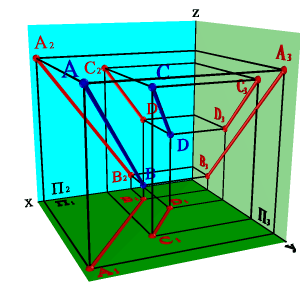
 3.19.
- Сурет. Параллель түзулер
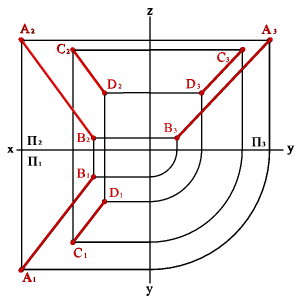
3.19.
- Сурет. Параллель түзулер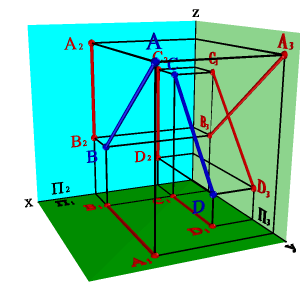
 3.20.
-
Сурет.
Профиль проекциялар жазықтығына
параллель түзулер.
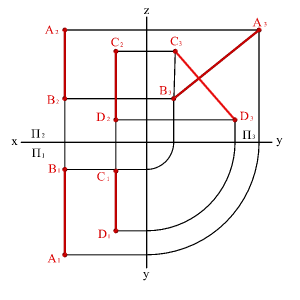
3.20.
-
Сурет.
Профиль проекциялар жазықтығына
параллель түзулер.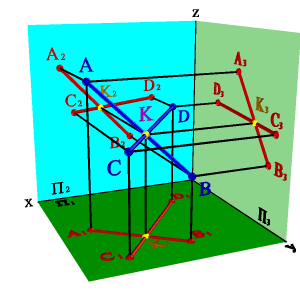
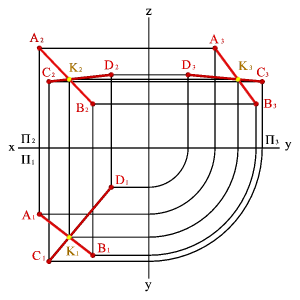 3.21.
-
Сурет.
Қиылысатын түзулер
3.21.
-
Сурет.
Қиылысатын түзулер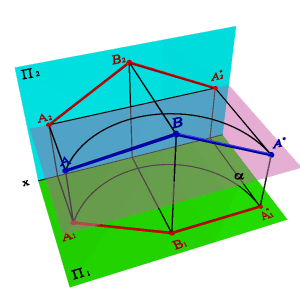
 4.4.
- Сурет.
Горизонталь
проекциялар жазықтығына препендикуляр
өс бойынша айналдыру әдісімен
кесіндінің шынайы өлшемін анықтау
4.4.
- Сурет.
Горизонталь
проекциялар жазықтығына препендикуляр
өс бойынша айналдыру әдісімен
кесіндінің шынайы өлшемін анықтау